一种新颖的第二类Stirling数公式证明

李新社， 姚俊萍

（西安高新技术研究所，陕西西安 710025）

0 引 言

Stirling数在资源分配、微积分应用、有限集合划分等方面都有着广泛的应用，所以诸多学者在论文或编著中都研究和讨论Stirling数，但由于Stirling数复杂，计算公式难以推导，所以证明过程难以掌握接受。文献［1］通过7个引理和数学归纳法完成了第二类Stirling数公式的证明，篇幅长达两个版面，推导变化异常复杂；文献［2］通过不完全归纳法进行猜想Stirling数公式，然后，通过大量的组合计算变换完成了第二类Stirling数公式的证明，关键是猜想的逻辑难以论述，不易阅读、理解和掌握；文献［3］给出了一些特殊情况下的Stirling数计算公式，缺乏普遍性，难以推广使用；文献［4］通过数学归纳法完成了第二类Stirling数公式的证明，但证明过程长，而且只回答了公式的正确性，未回答公式的模型构造过程。文中根据函数定义、满射函数特性、容斥原理、逐步淘汰原理、排列组合理论等，讨论分析了满射函数与有限集合划分的关系，基于逐步淘汰原理给出了有限集合间满射函数个数的计算公式，最后由满射函数个数计算公式推导出含有m个元素的有限集合划分成n个非空子集的种类数计算公式，从而完成了第二类Stirling数公式的一个既简单又易接受的证明过程。

1 基本概念与基本原理

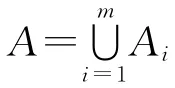
定理1 设π是非空集合A上的划分，R是A上的等价关系，那么π诱导出R当且仅当R诱导出π。

定理2（容斥原理） 设A1，A2，…，An为有限集合，则

定理3（逐步淘汰原理） 设A1，A2，…，An为有限集合S的子集，则

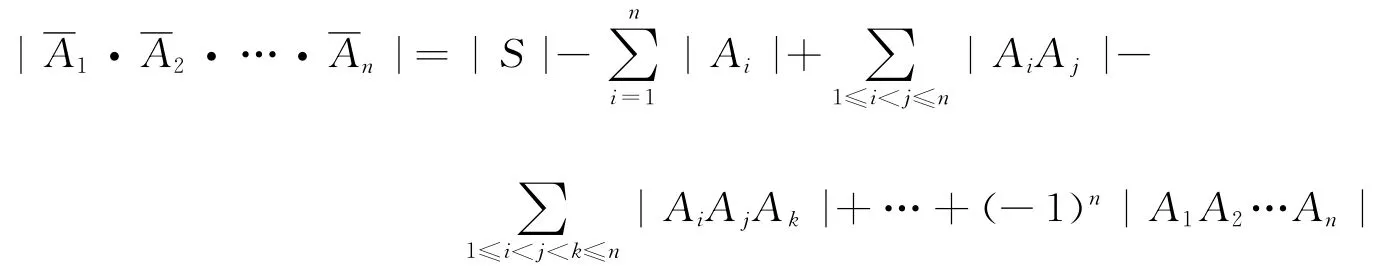
定义2 设A，B是两个集合，如果按照某种对应法则f，对于集合A中的任何一个元素，在集合B中都有唯一的元素和它对应，这样的对应叫作从集合A到集合B的映射。记作：f：A→B。

定义3 设f是A到B的一个映射，若对B中的每一个元素y，都存在x∈A使得y＝f（x），则称f是A到B的一个满射。

根据文献［6-7］，Stirling数的本质在于求解有多少种方法可将一个含有m个元素的有限集合划分成n个非空的子集，记为S（m，n）。根据这一含义显然有

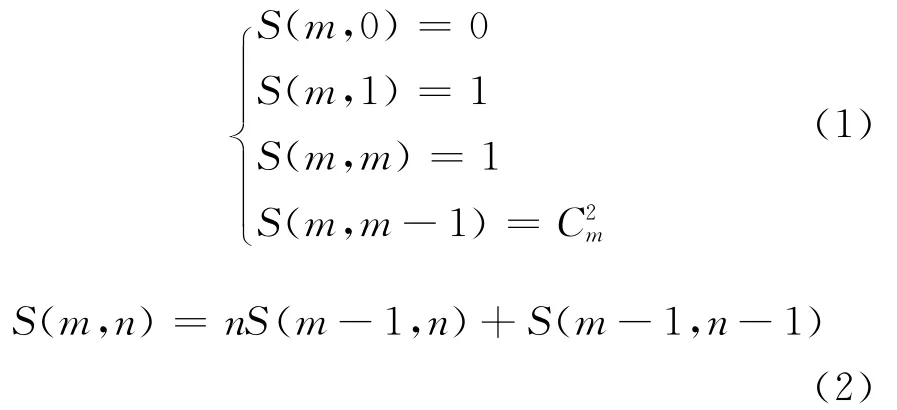
S（m，n）数列通项计算公式为

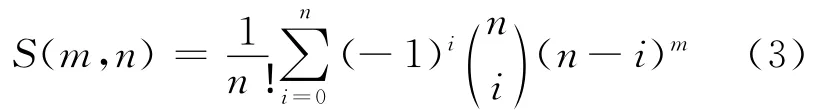
现在的问题是上面这个通项计算公式是否正确？如何得来？正如引言所论述，文献［1-4］的作者和其他一些国内外学者都给出了一些研究成果，但推导过程复杂，难以理解和掌握。下面基于定义1、定义2、定义3、定理1、定理2、定理3等展开研究。

2 有限集合划分与有限集合间满射函数的关系

设f：A→B为A到B的任意一个满射函数，其中，｜A｜＝m，｜B｜＝n，m＞n，规定A上的二元关系R为

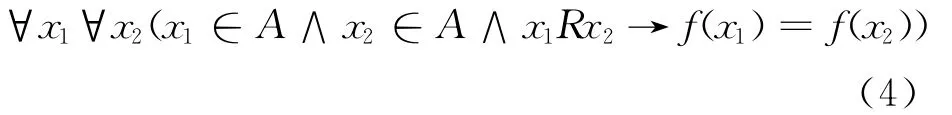
不难证明R具有自反性、对称性和传递性，是A上的一个等价关系。这样由一个满射函数就确定了一个等价关系，而基于这个等价关系正好将A可划分成n个非空子集。又根据有限集合上的等价关系与有限集合的划分是一一对应的（定理1），所以满射函数与划分之间有对应关系，但注意到等价关系定义中强调的是函数值相同，未强调对应的具体值，也就是说函数值之间可以互换并不改变划分结果，因此，根据函数定义和排列组合原理可以得出n！个函数对应一个划分。换句话说，如果求得A到B的满射函数个数，就可求得将一个含有m个元素的有限集合划分成n个非空子集的方法数。

3 有限集合间满射函数个数的计算公式

同上，仍然设f：A→B为A到B的任意一个满射函数，｜A｜＝m，｜B｜＝n，m＞n。

根据满射函数定义，B中每个元素都要被映射到，直接求出所有满射函数个数有困难。但从A到B的所有函数中除去B中至少有一个元素未被映射到的函数，就可得到A到B的所有满射函数。而这正是容斥原理（定理2）和逐步淘汰原理（定理3）解决问题的思路和方法。

首先根据定义2易知，A与B之间可构造的函数有nm个，其次B中有一个元素未被映射到的函数个数为（n－1）m个；B中有2个元素未被映射到的函数个数为（n－2）m个；…；B中有i个元素未被映射到的函数个数为（n－i）m个；B中元素都未被映射到的函数个数显然为0，即（n－n）m。由定理3得可构造的满射函数个数为

即

4 第二类Stirling数公式与验证

根据“2”和“3”的讨论，立即可以得出

对于得出的公式，显然S（m，0）＝0，S（m，1）＝1，S（m，m）＝1，S（m，m－1）＝是成立的，符合Stirling数的含义。

至于S（m，n）＝nS（m－1，n）＋S（m－1，n－ 1），结合

也可验证是成立的。

5 结 语

通过满射函数、等价关系、划分、逐步淘汰原理等的相互联系，给出了第二类Stirling数公式证明过程。该证明过程不仅揭示了第二类Stirling数公式的来源，而且从另一个方面回答了其正确性，有助于对第二类Stirling数本质含义的理解和大力推广使用。

［1］ 任逸.第二类Stirling数的一个计算公式及其证明［J］.数学通报，2008，47（3）：59-60.

［2］ 杨雅琴.第二类Stirling数计算公式的一种证明［J］.青岛科技大学学报：自然科学版，2009，30（4）：91-93.

［3］ 王红，杨雅琴，王艳辉.第一类Stirling数和第二类Stirling数的关系式［J］.高师理科学刊，2008，28（6）：37-39.

［4］ 吴学澄.计算第二类Stirling数的公式的证明［J］.东南大学学报：自然科学版，1987，17（3）：159-161.

［5］ 方世昌.离散数学［M］.西安：西安电子科技大学出版社，2005.

［6］ 卢开澄.组合数学［M］.北京：清华大学出版社，1999.

［7］ Danie I A Cohen.Basic techniques of combinatorial theory［M］.［S.l.］：John Wiley ＆Sons Inc，1979：107-119.