伪随机编码调制线性调频波的MIMO超声测量方法

李鹏，尹杰，王银娟

(1.南京信息工程大学 江苏省气象探测与信息处理重点实验室，江苏 南京 210044；2.南京信息工程大学 电子与信息工程学院，江苏 南京 210044)

超声测量方法因其高性价比、结构简单、超声波良好的声学特性(即超声波方向性好，传输过程衰减小，反射性能强等)等特点被广泛应用于材料工业、原油化工、气象等各个领域。然而，测量准确性方面还有待进一步提高，尤其是在起伏界面和高噪声情况下的距离测量方面。为了进一步提高测量准确性，超声测量方法在发射信号、渡越时间(TOF)估计、回波信号处理等方面被加以研究，并取得了一定的进展。在发射信号及回波信号处理方面，线性调频波被应用到超声液位测量中，并结合匹配滤波技术提高液位测量的准确性[1-2]；在TOF估计方面，利用无损卡尔曼滤波处理超声回波信号，得到回波信号的包络线，同离散扩展卡尔曼滤波相比，TOF估计精度得到提高的同时减少了计算量[3]。我们研究超声测量方法并致力于提高其测量准确性，是因为在气象中的应用需求，比如雨量、蒸发量、雪深等等的测量。我们提高超声测量方法测量准确性的着手点是采用稀疏超声阵列的MIMO测量系统，这种方法在雷达、通信中得到应用研究并取得很好的研究进展[4-5]，因而，被借鉴到我们的超声测量中。

平衡Gold码以其优良的相关性(即尖锐的自相关性与平坦的互相关性)作为地址编码被广泛应用于码分多址通信系统中[6]，本文采用平衡Gold伪随机码调制线性调频波(平衡Gold-LFM)进行信号发射，以此来实现MIMO超声阵列测量。通过仿真实验对所提出的方法及其关键方面如通道分离进行验证，实验结果证明平衡Gold-LFM复合信号具有良好的相关性，能够较好地实现通道分离；在不同信噪比情况下的仿真结果说明该方法不仅可行，并且测量准确性有相当大的提高，特别是抗噪声性能较线性调频波的激励方法有很大改善。

1 测量原理

1.1 超声阵列结构

本文提出的超声测量方法主要包括四个关键技术：超声阵元阵列、信号模型、通道分离及波束形成，其中波束形成采用常规的延时求和波束形成。通过多个发射阵元同时发射不同的平衡Gold-LFM复合信号，多个接收阵元同时接收回波，在接收端对回波进行通道分离，对分离后的回波信号进行波束形成处理[7-8]，来实现MIMO超声阵列测量。而在MIMO超声阵列测量中，传感器阵列的设计是关键，它的性能优劣决定了系统的性能。我们在这里借鉴MIMO雷达中天线阵列的研究成果，采用等效虚拟阵元[4]的设计方案。如图1所示，采用一组接收阵列稀疏排列于两组发射阵列中间作为超声测量阵列，对于收发分置的阵元可根据等效相位中心近似原理[9]将其简化为收发同置的阵元，由一对发射接收阵元的中心位置(虚拟阵元位置)等效，再结合超声发射接收阵元间距的设计，由M个发射阵元和N个接收阵元形成M×N个均匀分布的相互独立通道的阵元阵列的准则为：如果设定虚拟阵元的间距为d，则每组发射阵列的阵元间距为dT=2×d，接收阵列的阵元间距为dR=M×d，每组发射阵列与接收阵列边缘的间距为d，这样形成的超声阵列的实际物理尺寸为(MN-M-2)d。与传统的相控阵相比，同样形成M×N个独立的通道，等效虚拟阵元的方法只需M+N个阵元，降低了系统的复杂度和成本。

图1 基于平衡Gold-LFM复合信号的超声阵元阵列的结构图

1.2 平衡Gold-LFM复合信号模型

平衡Gold码以其优良的相关性作为地址编码被广泛应用于码分多址通信系统中，线性调频信号作为发射信号可以在增加探测距离的同时获得较好的距离分辨率。本文采用不同的平衡Gold码调制线性调频信号的相位赋予每个超声发射阵元唯一的信号，提高回波信号的通道分离特性。假设超声阵列由M个发射阵元和N个接收阵元构成，则发射阵元i的信号表达式如式(1)：

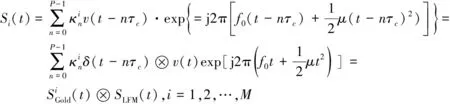
(1)

则接收阵元k的回波信号的表达式如式(2)：

(2)

其中，αi为超声回波信号衰减幅度，τki为第i个发射阵元发射的信号到目标，再经目标到接收阵元k的传播时间。

1.3 通道分离

匹配滤波是一种信号分离的好方法，本文采用的发射信号具有优良的相关性，此时，匹配滤波等效于相关处理[10]。对接收阵元，用Sj(t),j=1,2,…,M分别与xk(t),k=1,2,…,N进行相关处理分离出每个虚拟阵元的回波信号，以便进行后续的波束形成。通道分离后输出信号的表达式如式(3)：

(3)

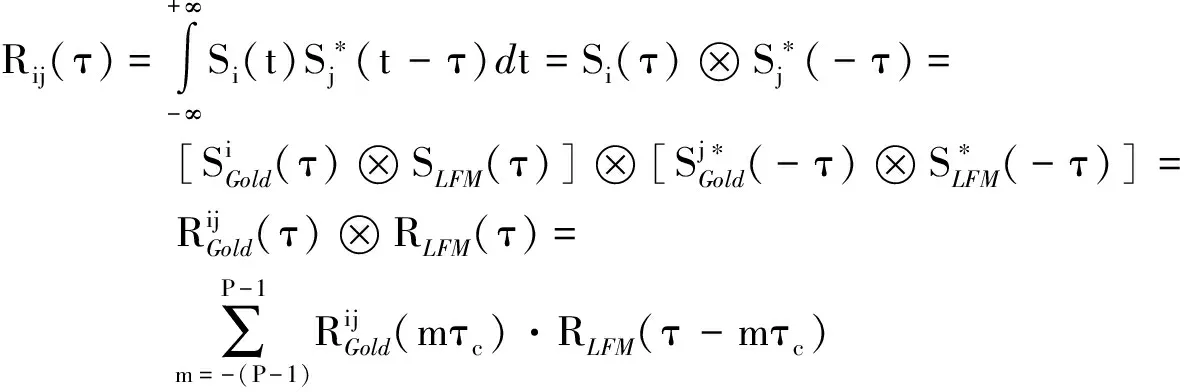
(4)

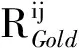
(5)

(6)

当i=j时，可得到相应的复合信号的自相关函数：

(7)

m=0时，可得：

(8)

由式(4)和式(6)可以看出，复合信号相关处理后的包络由近似辛格函数与平衡Gold码的相关性决定，平衡Gold码有较小的自相关旁瓣和互相关值，确保了复合信号的正交性，有利于实现合成回波的通道分离。通道分离后的输出信号主要由复合信号自相关函数决定，因此可由式(8)看出复合信号的距离分辨率由通道分离后输出信号的近似辛格函数决定，其值为1/B。

2 仿真实验与分析

2.1 平衡Gold-LFM复合信号的通道分离性能仿真

仿真实验采用4个发射信号，线性调频信号的中心频率设为300 kHz，带宽为60 kHz，为简便，本文优化一组平衡Gold码进行实验，如表1，码长为127，码宽为32 μs。通过对4个超声发射信号进行自相关和互相关处理来检验平衡Gold-LFM复合信号通道分离性能。

采用表1中的平衡Gold码调制线性调频信号的相位，所得信号的通道分离性能如图2(每个子图坐标一致)。

图2 平衡Gold-LFM复合信号通道分离性能

图2中主对角线位置的子图为信号Sm(t),m=1,2,3,4(m=n时)的自相关值，其他位置的子图表示信号Sm(t),m=1,2,3,4与信号Sn(t),n=1,2,3,4(m≠n时)的互相关值，每个子图的横坐标表示时间，纵坐标表示归一化幅度。优化得到的平衡Gold码调制线性调频信号的平均自相关旁瓣峰值(ASP)为0.1634或-15.73dB，平均互相关峰值(CP)为0.1745或-15.16dB，可以看出本文的复合信号具有良好的相关性能，即具有尖锐的自相关性和平坦的互相关性，尖锐的自相关性有助于提高测量的准确性，平坦的互相关性有助于接收端中不同发射信号产生的回波成分的通道分离。

2.2 测量仿真

气象中雨量、雪深等的测量可看成起伏界面的距离测量，为简单起见，文中通过单点目标的仿真检验平衡Gold-LFM复合信号MIMO超声测量方法的可行性。采用图1中的4个发射阵元和4个接收阵元的MIMO超声阵列，取阵列的中心点为坐标轴原点，虚拟阵元间距取d=15 mm，线性调频信号的中心频率设为300 kHz，带宽为60 kHz，平衡Gold码选用表1中的编码，单点目标角度设置在0度，距离设为0.35～0.5 m。

采用平衡Gold-LFM复合信号的MIMO超声测量方法对单点目标重复测量30次，改变单点目标的距离，重复上述的实验，在相同的条件下采用线性调频信号激励进行仿真，统计得到两种不同激励方式的绝对平均误差如图3(a)，可以看出本文采用的平衡Gold-LFM复合信号激励方式是有效可行的。图3(b)为平衡Gold-LFM复合信号局部测量距离(0.4～0.45 m)的误差放大图，可以看出本文采用的平衡Gold-LFM复合信号MIMO超声测量方法的测量误差在0.08 mm范围内波动，说明该方法不仅是可行的，而且能够进一步提高测量准确度。

图3 平衡Gold-LFM复合信号激励与线性调频信号激励的测量误差

进一步分析平衡Gold-LFM复合信号MIMO超声测量方法在不同信噪比情况下测量的准确性。点目标位置设在(00,0.5 m)，信噪比变化范围取-30～15 dB，为了检验平衡Gold-LFM复合信号的抗噪声性能，在相同仿真条件下采用线性调频信号的激励方式与之进行对比实验，得到的抗噪声性能如图4。

图4 平衡Gold-LFM复合信号激励与线性调频信号激励的抗噪声性能

可从图4(a)中看出，采用平衡Gold-LFM复合信号MIMO超声测量方法能在信噪比低至-30 dB的情况下可靠工作，其抗噪声性能明显优于线性调频信号激励的方法；为了更清楚地观察以上两种激励的测量误差曲线的变化规律，图4(b)为图4(a)的纵向放大图形，显示测量误差在0.4 mm范围内的误差曲线，能看出在信噪比变化时本文采用的超声测量方法的测量误差在0.05 mm范围内波动，具有很好的测量准确性；图4(c)列举了信噪比为0 dB,-10 dB,-20 dB,-30 dB情况下本文所用超声测量方法得到的测量结果图，随着信噪比的降低，图中距离旁瓣逐渐升高，这会影响目标的分辨性能，在超声成像时需要进行相应的旁瓣抑制处理。

3 结 论

本文提出平衡Gold-LFM复合信号的MIMO超声测量方法，通过理论分析和仿真实验证明了平衡Gold-LFM复合信号具有尖锐的自相关性和平坦的互相关性，能较好地实现回波信号的通道分离，又进一步仿真验证了平衡Gold-LFM复合信号MIMO超声测量方法测量的准确性，其测量误差在0.08 mm范围内波动，同时在高噪声情况下仍能可靠工作，抗噪声性能优于线性调频信号激励方式。因此，平衡Gold-LFM复合信号MIMO超声测量方法是有效并可行的，这种方法可以应用到雨量、雪深和蒸发量等的测量方面，具有广阔的发展前景。

参考文献：

[1]臧怀刚，李刚，王丹丹.应用线性调频信号的智能超声液位仪[J].传感器与仪器仪表，2010，26(3-1)：120-122.

Zang Huaigang，Li Gang，Wang Dandan.Intelligent ultrasonic measure apparatus for liquid level based on linear frequency modulation signal[J].Sensors and Instrumentation，2010，26(3-1)：120-122.

[2]李鹏，冯彬彬，陈小晴，等.一种新的采用LFM波的超声液位测量技术研究[J].安徽大学学报：自然科学版，2013，37(3)：51-55.

Li Peng，Feng Binbin，Cheng Xiaoqing，et al.Study of a new ultrasonic liquid level measurement technology by using linear frequency modulated wave[J].Journal of Anhui University (Natural Science Edition)，2013，37(3)：51-55.

[3]Angrisani L，Baccigalupi A，Lo Moriello RS.Ultrasonic time-of-flight eatimation through unscen-ted kalman filter[J].IEEE Transactions on Instrumentation and Measurement，2006，55(4)：1077-1084.

[4]Huang Y，Brennan PV，Patrick D，et al.FMCW based MIMO imaging radar for maritime navigation[J].Electroma-gnetics Research，2011，115：327-342.

[5]Wang Wenqin, Cai Jingye.MIMO SAR using chirp diverse waveform for wide-awath remote sensing[J].IEEE Transactions on Aerospace and Electronic Systems，2012，48(4)：3171-3185.

[6]曾兴雯，刘乃安，孙献璞.扩展频谱通信及其多址技术[M].西安：西安电子科技大学出版社，2004.

[7]He Tian，Pan Qiang，Liu Yaoguang，et al.Near-field beamforming analysis for acoustic emission source localization[J].Ultrasonics，2012，52(5)：587-592.

[8]孙超.水下多传感器阵列信号处理[M].西安：西北工业大学出版社，2007.

[9]叶荫，刘光炎，孟喆.机载下视稀疏阵列三维SAR系统及成像[J].中国电子科学研究院学报，2011，6(1)：96-100.

Ye Yin，Liu Guangyan，Meng Zhe.Airborne downward-looking 3D-SAR systems and its imaging using sparse array antennas[J].Journal of CAEIT，2011，6(1)：96-100.

[10]Mahafza B R，Elsherbeni A Z.朱国富，黄晓涛,等，译.雷达系统设计MATLAB仿真[M].北京：电子工业出版社，2009.