机载雷达抗异步干扰脉冲的研究

乌伟, 邱宗明, 宋春林

(1.西安理工大学 机械与精密仪器工程学院，陕西 西安 710048; 2.北方信息控制集团，江苏 南京 211153)

进入21世纪以来，军用电子系统由综合化向集成化发展，通信、雷达、导航、电子仪器以及各种武器监控、目标识别及定位、军事指挥等方面均广泛地实现了信息化和智能化，这极大地提高了武器系统的综合效能。与此同时，雷达所处的电磁环境也越来越复杂。雷达在使用的过程中，总会收到很多来自自身或者外部的干扰。现代战争，如海湾战争、科索沃战争以及第二次伊拉克战争都已表明，雷达在复杂电磁环境下的抗干扰能力是影响现代战争胜负的决定性因素之一[1]。复杂的电磁环境决定了雷达必须具备抵抗多种电子干扰的能力。

脉冲干扰是机载雷达常收到的干扰样式之一。雷达收到的强干噪比干扰脉冲信号在时域呈冲击状，经频谱变换后，会导致二维距离-频率谱噪声基底的抬升，严重时会埋没真实目标的回波谱线，导致雷达性能下降甚至失效[2-3]。如何抵御这种强干扰脉冲的影响是工程实践中常遇到的棘手问题之一。脉冲干扰分为同步脉冲干扰和异步脉冲干扰。如果脉冲干扰在雷达回波中出现的时间与雷达系统定时稳定，则称为同步脉冲干扰，否则称为异步脉冲干扰。虽然干扰脉冲相对于真实目标回波信号来讲，其功率要大得多，但是对于机载雷达而言，地杂波的强度却是在所有回波中占绝对主导地位的。因此要进行干扰脉冲检测和剔除，必须首先进行地杂波的抑制处理。

1 机载雷达地杂波功率仿真[4-8]

假定地面是均匀反射的，即单位面积的等效杂波截面积仅与擦地角有关，杂波散射体所在的地球表面是一个平面。则由图1可知，杂波散射单元的微分面积可以表示为:

dA=dR×(R×dθ)

(1)

式中R表示散射单元到雷达的距离。

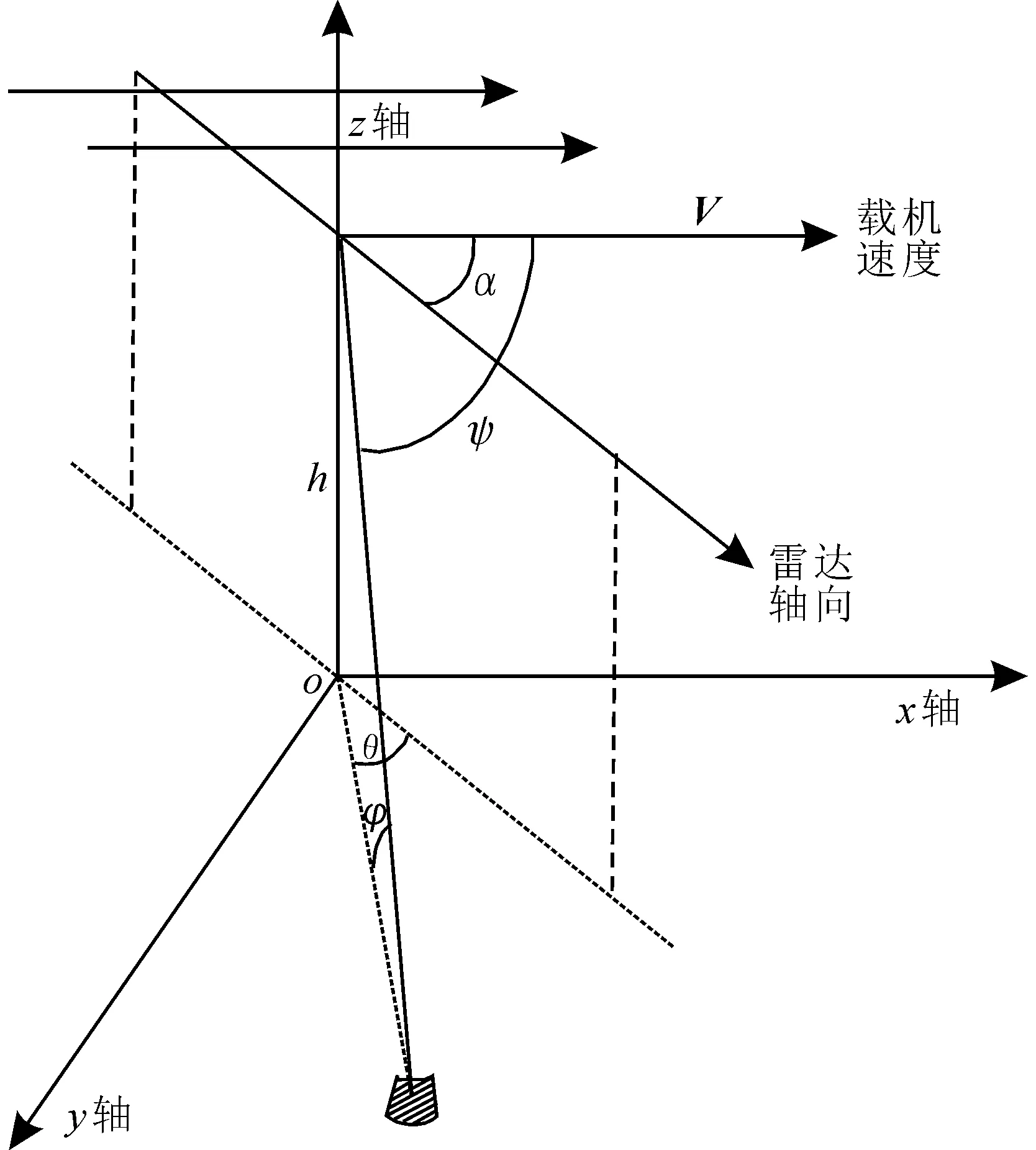
图1 杂波散射单元几何位置示意图

若散射单元的散射系数为σ0(在本文的假设条件下，σ0是φ的函数)，则其散射截面积可以表示为:

dσC=σ0dA=σ0dR×(R×dθ)

(2)

由雷达方程[9]可知，雷达收到的由该散射单元反射的回波的功率为:

(3)

式中Pav是雷达发射机的平均功率，Gt和Gr分别为天线的发射和接收增益，L为系统损耗因子，λ为雷达工作频率对应的波长。

该散射体回波的多普勒频率为：

“文艺片是票房毒药”已经成为业内心照不宣的默认事实，即使有名导、一线明星加持，也大多票房惨淡。有舒淇、张震加侯孝贤的《刺客聂隐娘》仅6140.5万票房，流量女王杨幂的《宝贝儿》止步于2471.2万票房，最近上映的《你好，之华》有岩井俊二、陈可辛加周迅的豪华班底，也仅仅收获8013.7万票房。“破亿”对绝大多数文艺片而言已经是可喜可贺，更多的文艺片徘徊在千万以下。

(4)

对于同一距离门上的回波，主杂波的展宽主要是由不同方位角上的地面散射体回波引起的。取fd对θ的微分，可得:

(5)

在计算杂波散射体时，考虑到散射体的面积,并且功率取值非负，因此将式(5)代人式(3)，可得:

dPC=

(6)

对于任意一个杂波散射单元(R,fd)，雷达接收到的杂波功率密度可以表示为R和fd的函数：

PC(R,fd)=

(7)

式中：

因此给定飞机和雷达系统参数，由式(7)就可以计算出雷达主杂波的输出功率。

2 主杂波的自回归模型估计和消除[10-13]

由第1部分的分析可知，主杂波是占据一定带宽且强度很大的正弦信号。要进行抗同频异步干扰的处理，首先就要尽量减弱由于主杂波的存在而导致的对干扰检测的影响。实际上，由于主杂波通常比干扰信号要大几十个分贝，因此若不进行杂波消除处理，是没办法进行干扰检测和剔除处理的。

线性预测方法或者称为自回归方法(AR)能有效地对正弦信号进行拟合。L阶AR预测模型的表达式[5]为:

(8)

式中ai为AR模型参数。

滤波器y(k)构成了一个预测误差残留滤波器，简称残差滤波器。

(9)

残差滤波器是一个全零点线性滤波器，滤波器的性能取决于x(k-1)，x(k-2)，…,x(k-L)对x(k)的逼近程度。由式(7)可知，主杂波的分布是距离相关的。若假定同一距离单元的主杂波回波信号是广义平稳的，并用最小方差作为一个评价标准，则由式(7)可得满足最小方差估计时的系数应满足方程(10)。

(10)

式中，ρi=E(x(k)x*(k-i))为x(k)的自相关函数，*表示取共轭。x(k-i)，i=1,2,…,L是同一距离门上所收到的不同时刻的脉冲回波信号。方程(10)称为Yule-Walker方程。

若雷达所接收到的脉冲总个数为N，不失一般性，这里不妨假定N能整除L+1。设M=N/(L+1),则ρi可以用式(11)来估计。

(11)

式中：

3 干扰脉冲检测与消除

设第r0号距离门上的第k0个脉冲回波存在干扰信号Jk0，而从(k0-L)到(k0+L)的脉冲回波上不存在干扰信号。设AR模型的系数为a1，a2，…，aL。另外，为了叙述方便，再定义a0=-1，则在使用残差滤波器之后，第k0到第(k0+L)个回波信号分别为：

z(k)=-ak-k0Jk0+y(k)+U

(12)

式中k=k0,…,(k0+L)，y(k)为残差滤波器输出的杂波剩余，U为残差滤波器输出的系统噪声剩余。

可用判决因子式(13)来判定干扰是否存在以及干扰所在的位置。

(13)

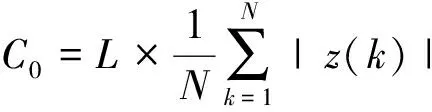
若γ(k0)>γ0，并且满足γ(k0)>γ(k0-1)，γ(k0)>γ(k0+1)，则可判定第k0个脉冲回波存在干扰信号；否则，认为第k0个脉冲回波不存在干扰信号。

当判断出干扰脉冲所在的回波位置之后，可以使用等强度噪声信号或者用周围的信号结合杂波中心的估计值来重构回波信号，以替代干扰脉冲所在的回波信号，从而达到剔除干扰脉冲的目的。

至于AR模型中参数L的选取，则需要根据干扰密集程度等一些先验知识来进行了。原则上，由干扰密度程度决定L的取值方位，从而影响干扰判决误判的概率。

4 实验结果及分析

设载机的高度为3 000 m，载机的速度为200 m/s，速度矢量方向为正东，雷达天线的轴向矢量与速度矢量方向重合，雷达天线采用收发相同的天线，雷达波长为3 cm，天线最大增益32 dB，天线方位向的辐射方向图由阵元间距等于波长、阵元个数为50的不带加权的线性阵列天线进行仿真，天线波束宽度5度，雷达发射机的平均功率为100 W。雷达系统损耗5 dB。地面的后向散射系数为0.15。杂波中心到雷达的距离为20 km，雷达天线中心指向为20度，雷达距离向采用门门宽1 μs。雷达发射的脉冲个数为128。则由式(7)可得20 km处对应的天线主瓣照射产生的各频率门的杂噪比(见图2)。

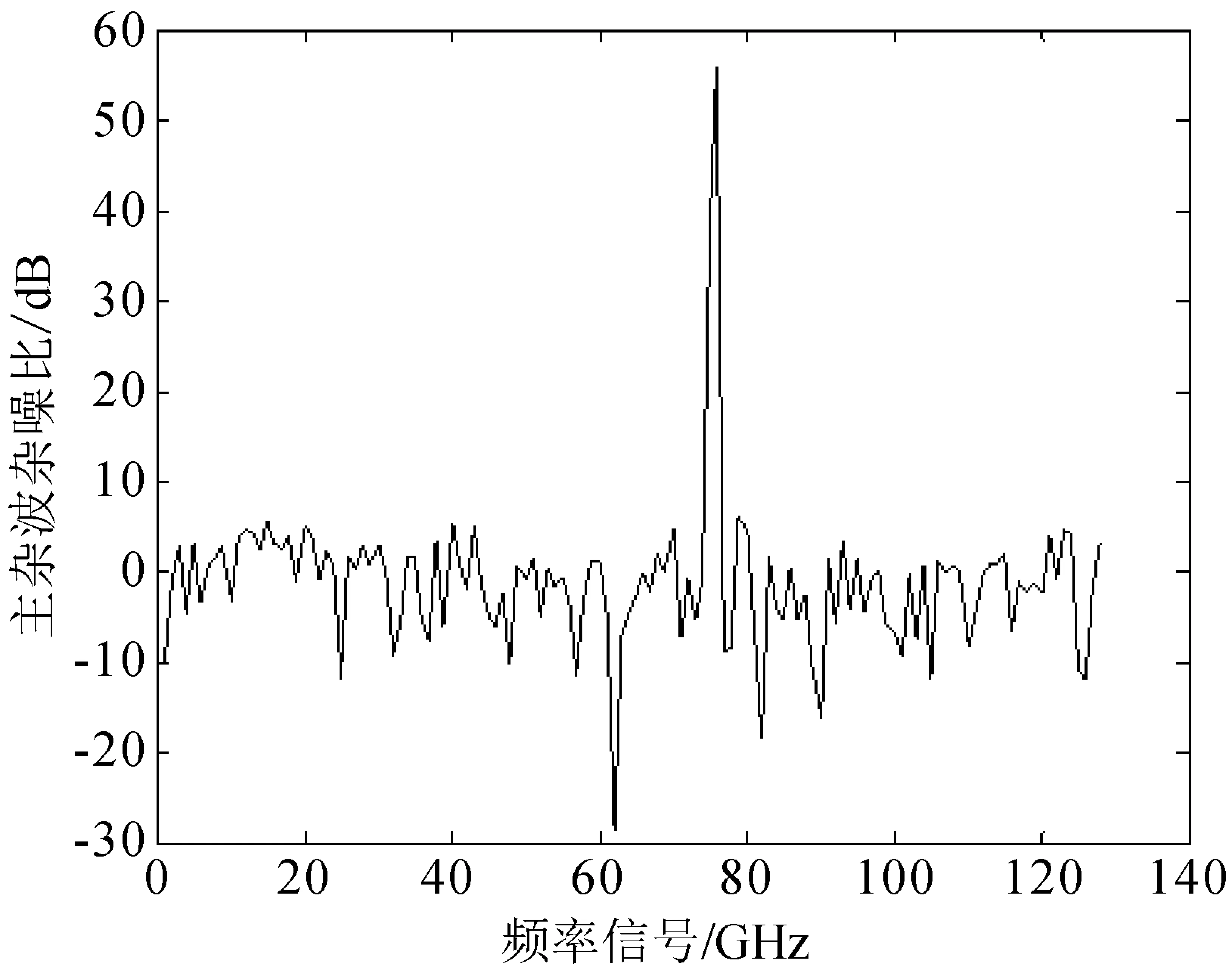
图2 主杂波的杂噪比

然后通过IFFT之后，得到主杂波的时域信号，再在第70个、第90个、第110个时域回波信号中分别添加干噪比为15 dB的干扰脉冲后，得到加干扰后的主杂波时域采样图(见图3)。

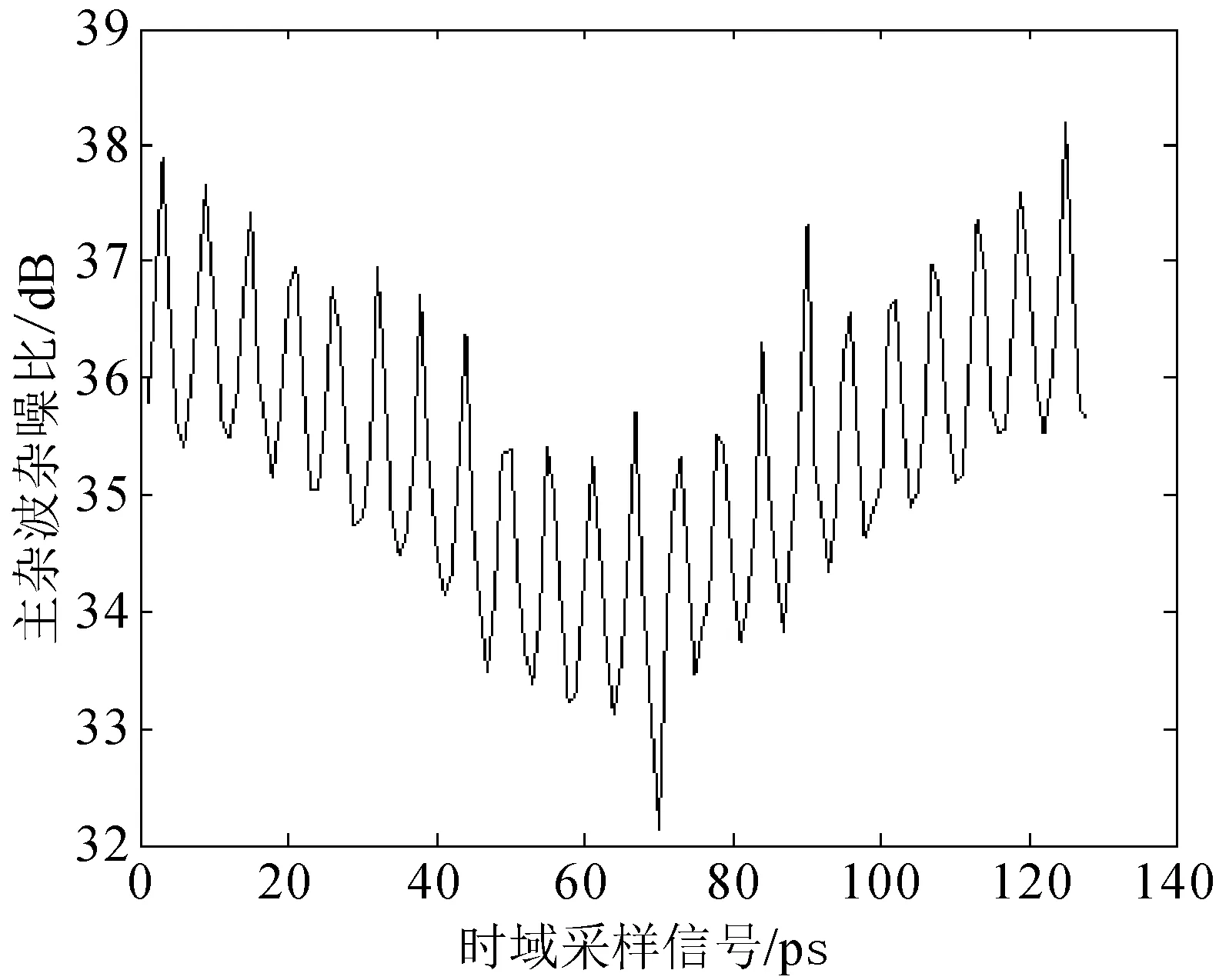
图3 加干扰后的主杂波时域图

对主杂波时域信号使用2阶AR模型进行滤波后得到的残差滤波器输出图如图4所示。从图4可以看出，在使用基于AR模型的残差滤波器之后，干扰脉冲凸显了出来。然后再使用干扰判决滤波器后，得到的判决因子图如图5所示。从图5可以看出，在使用判决因子之后，就能够精确的判断干扰脉冲的位置，并且判决因子的大小取决于干扰脉冲的强度。

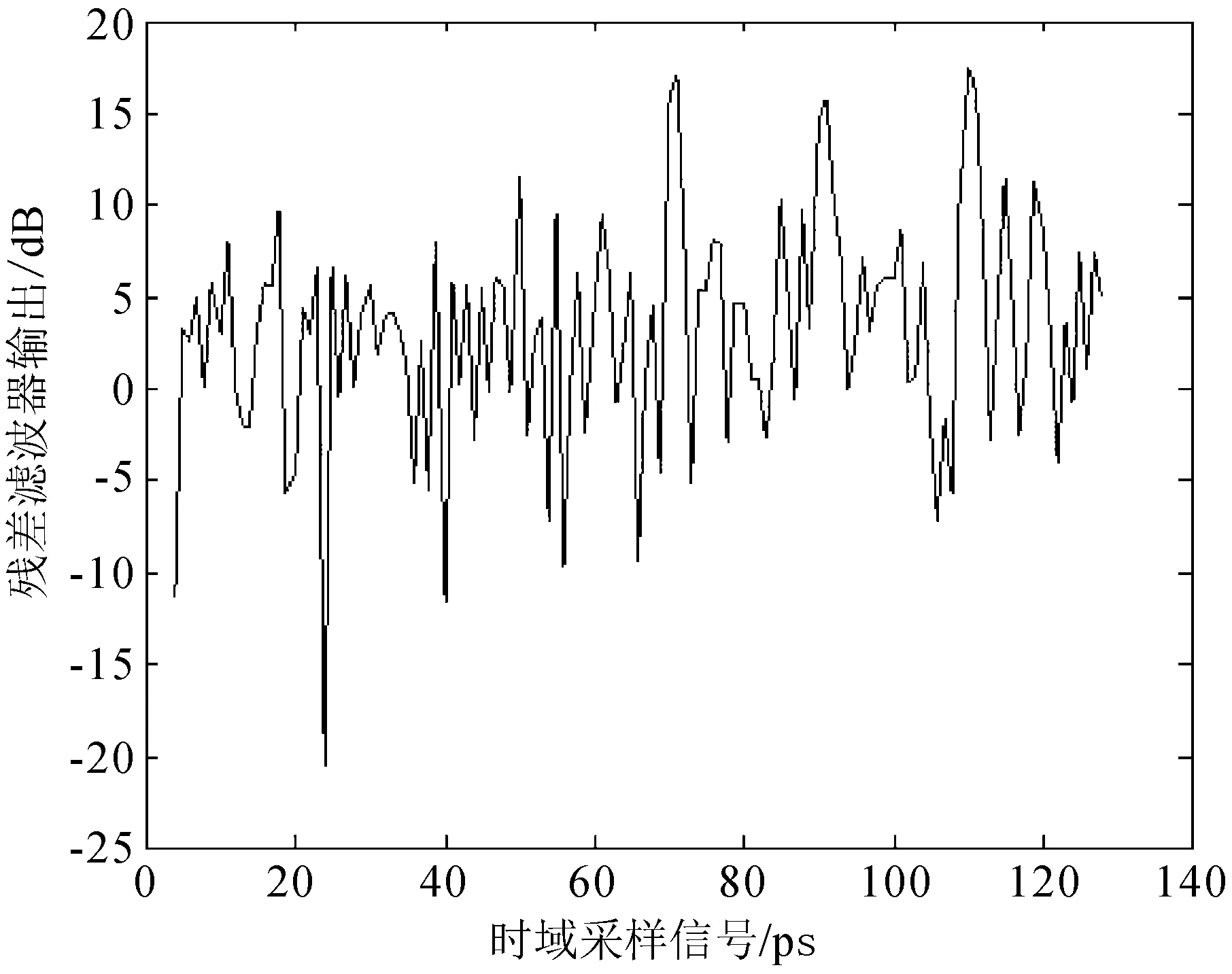
图4 残差滤波器输出

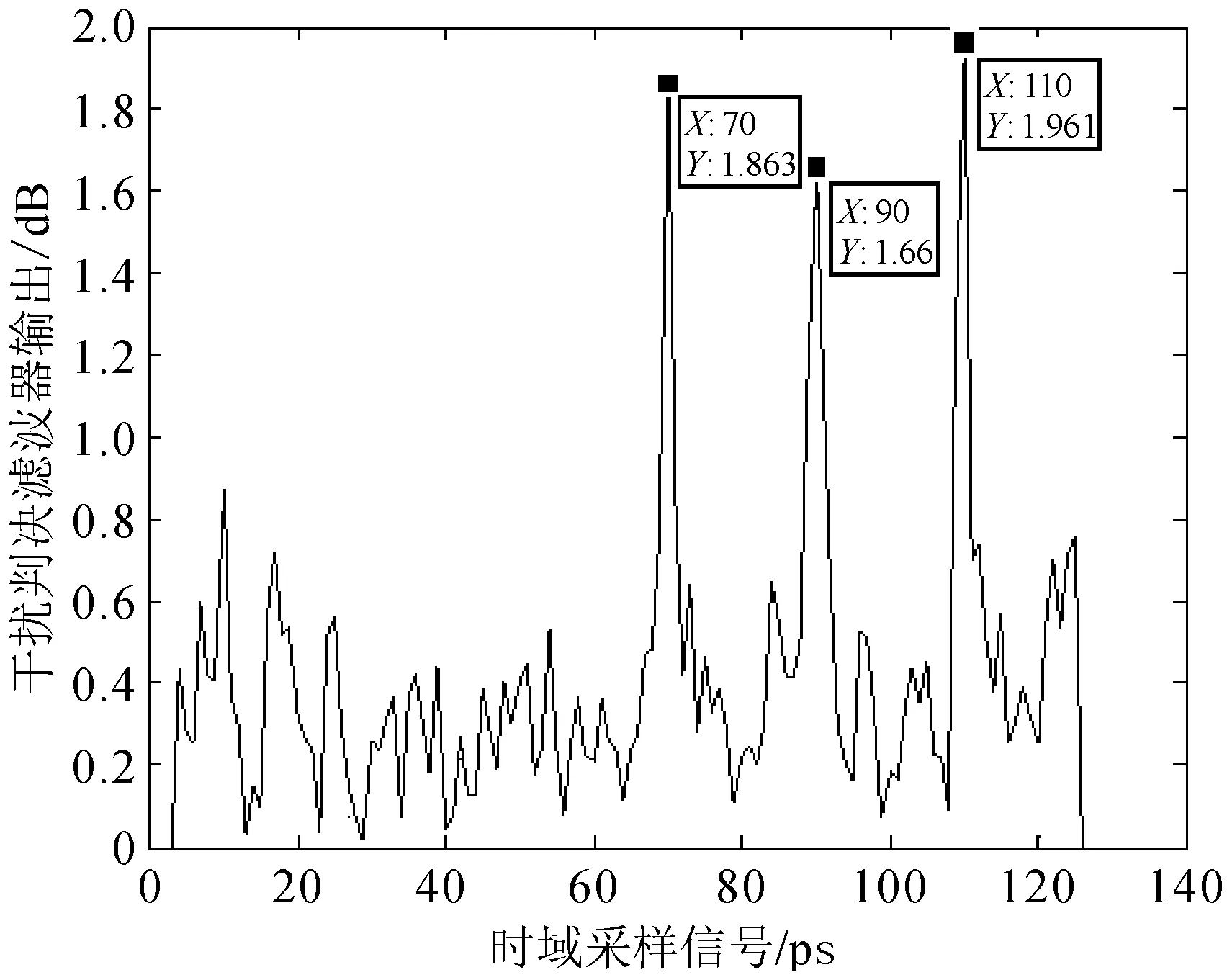
图5 干扰存在判决因子图

5 结 语

本文研究了机载雷达的异步干扰脉冲的检测和剔除处理。文中首先利用雷达方程给出了机载雷达地杂波在二维距离-频率谱上的分布，然后利用AR模型构建了一个残差滤波器,用以减弱地杂波对干扰脉冲检测的影响，接着给出了干扰存在的判决处理。仿真结果表明，该方法可行且有效。

参考文献:

[1] 丁鹭飞. 雷达原理[M]. 第四版. 北京：电子工业出版社，2009.

[2] 李洁群,王建国. 合成孔径雷达的干扰参数分析[J]. 实验科学与技术,2006,4(2):111-114.

Li Jiequn,Wang Jianguo. Analysis of jamming to SAR[J]. Experiment Science & Technology,2006,4(2):111-114.

[3] Wu Yuqing,Sun Xiaofeng. A compound interference with distributed interference and false track interference for radar networking[C]//ICSEM,Chengdu,2012:318-321.

[4] Liu Tao，Zhang Yong，Luan Jinlong. A ground clutter computation procedure for airborne pulse Doppler radars[C]//2009 IET International Radar Conference. Guilin:IET Press，2009.

[5] Pan Liang，Zhang Jun，Fan Hongqi. A new method for computing ground clutters based on equal area partition idea[J]. Modern Radar，2005，27(2):47-63.

[6] Zhang Chuncheng，Ge Jianjun，Luo jian，et al．Analysis of ground clutter characteristics of airborne forward looking pulse Doppler radar in high PRF[C]//2006 International Conference on Radar.Shanghai:IEEE Press，2006.

[7] Fan Haiju，Li Jingwen． Simulation of ground clutter of air-borne PD radar based on fluctuant RCS[J]. Radar Science and Technology，2005，3(1):25-30.

[8] Browning D J, Summers J E.Computer modelling of ground clutter in airborne radar[C]//IEE Colloquium on Radar System Modelling,London: IEE Press，1998.

[9] 李圣衍，胡东，周宏宇,等. 雷达组网的干扰技术研究浅谈 [J]. 电子工程师,2006,32(11):4-6.

Li Shengyan,Hu Dong,Zhou Hongyu,et al. The interference of radar networking technology research,discussion[J]. Electronic Engineer,2006,32(11):4-6.

[10] Satoru Goto, Masatoshi Nakamura, Katsuji Uosaki. On-Line spectral estimation of nonstationary time series based on AR model parameter estimation and order selection with a forgetting factor[C]//IEEE,1995:519-522.

[11] Mateo Aboy,Oscar W Marquez, James McNames, et al. Adaptive modeling and spectral estimation of nonstationary biomedi-cal signals based on Kalman filtering[J].IEEE Trans on Biomedical Engineering, 2005,52(8):1485-1489.

[12] Yuri I Abramovich, NicholasK Spencer, Michael D E Turley. TVAR models for multiple radar observations [J]. IEEE Transactions on Signal Processing, 2007, 55(4):1298-1310.

[13] Abdullah Alzaman,Mohammed Ferdjallah, Ahmed Khamayseh. Muscle fatigue analysis for healthy adults using TVAR model with instantaneous frequency Estimation[C]//Proceedings of the 38th Southeastern Symposium on System Theory,US,IEEE,2006:44-47.