期刊R-后验影响因子研究*

■张学梅

苏州市职业大学图书馆，苏州致能大道106号 215011，E-mail：phygreen@hotmail.com

影响因子（impact factor，简称IF）最早由加菲尔德于1955年提出，最初目的是为科学家进行科研活动检索参考文献提供一种新途径［1］。1972年，加菲尔德又提出被引量能够反映出一种期刊的重要性大小，但同时也指出，有一些期刊，尽管很少被引用但却同样非常重要［2］。此后，影响因子概念在学术界逐渐流行开来，不但成为评价科技期刊的一种重要指标，还被广泛用于科学家个人、科研机构等对象的评价之中，成为众多科学家研究的热点课题之一［3］。而对影响因子的效用，人们褒贬不一，许多科学家认为影响因子具有各种局限性，如：影响因子只适用于评价期刊整体而不适用于评价单篇论文［4］、不能跨学科进行期刊评价［5］、在某些特定学科领域中无法发挥评价效果［6，7］等等。为了克服影响因子的上述不足，很多新的理论和方法被提出来以试图代替或修正期刊影响因子［8-10］。如：Kuo和Rupe为能够消除期刊的短期表现，提出可靠性影响因子，即 R-影响因子［10］。 最近，Patricia等人［11］为解决期刊影响因子对某一种期刊的评价可能存在短期内产生分数变化过大这一局限性，提出了基于贝叶斯理论的后验影响因子（即IFPI）。由于R-影响因子仅考虑到某一年期刊的影响因子JIF和表示较长时间的数据-被引半衰期，却没有考虑相邻年份期刊JIF数据，而后验影响因子IFPI虽考虑了的期刊相邻年份的JIF，但没有考虑较长时间内期刊的数据。

综上所述，传统影响因子JIF只考虑期刊短期内（2年）的数据、R-影响因子没有考虑相邻年份期刊JIF数据以及基于贝叶斯理论的后验影响因子IFPI没有考虑较长时间内期刊的数据。为降低以上因子容易受到人为因素控制这一现象，本文将结合Kuo和Patricia等人的理论，提出一种既包含可靠性影响因子（R-影响因子），又包含基于贝叶斯统计理论的先验影响因子的新影响因子，即R-后验影响因子。本文首先简单介绍R-后验影响因子的原理，为检验该影响因子的适用性，对物理学领域34种JIF≥3.0高质量期刊进行了实证研究，结果证明此影响因子对评价同一领域的期刊具有适用性。

1 R-后验影响因子模型

这里z（z≥2）表示计算过程中所选引文窗口的大小（一般为2年或5年，相应表示2年影响因子或5年影响因子），ny表示第y年之前z年内（即｛y-z，...，y-1｝）期刊刊载的论文总量，nc，y表示这 ny篇论文在第y年中获得的总被引量。

根据Kuo和Rupe等人定义的R-影响因子［10］可表示为：

设由JCR收录的期刊在｛y-z，...，y-1｝年间发表的全部论文组成样本Ω，随机变量X：Ω→Z+，ω→X（ω）=x，即某一篇论文ω在第y年间获得的总被引量；为研究方便，进一步设定x大小依赖于该篇论文所刊载的期刊“质量”，定义为该篇论文发表在“质量”为θ（为一未知量，本文中指JIF值）期刊上，且在第y年得到x次引用的概率。因期刊影响因子概率分布一般呈指数分布［12］，于是可设随机变量X在(θ0，θ)1⊂｛θ∈R：aθ2+bθ+c和g()θ＞0｝区间内指数型概率密度函数的一般表达式为，其中g()θ和h()θ是满足以下条件连续可微的实数函数：［12］

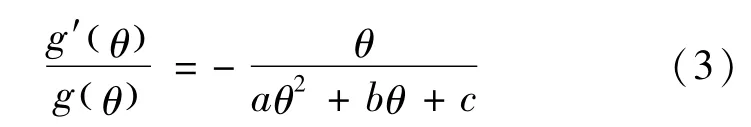
设样本 Xi=｛x1， ...， xny｝，i∈ JCR，xi为第i种期刊在｛y-z，...，y-1｝年之内发表的论文在第y年获得的总被引量，则于是基于样本Xi的似然函数：

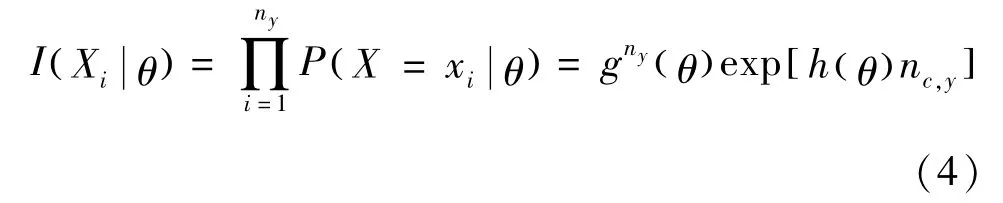
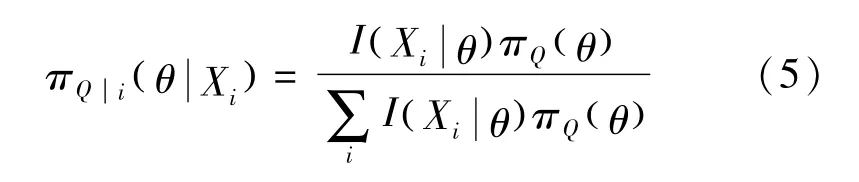
若选用参数θ的先验概率为

πQ()θ表示以前的可靠度；随机变量Q：JCR→R+，Q（i） =θ表示期刊i的质量指标为θ，它描述某篇论文的被引量。其中α＞3a（本文中a=0）且则后验概率

第二天下午，颜真卿又来方便时，抱着竹树摇头晃脑沉思入厕，竹根全断，竹子一松，他自己是猝不及防，破茅而出，直坠水潭，好容易一个千金坠定住身形，那边东方宇轩刚好路过，慌忙将鞋袜皆湿的一代文曲星拉上来。

根据 Chen等人的结论［13］，可得到：

为便于与传统期刊影响因子JIF进行比较，需定义两个新的影响因子分别为先验影响因子（prior impact）IFPO和后验影响因子 （posterior impact）

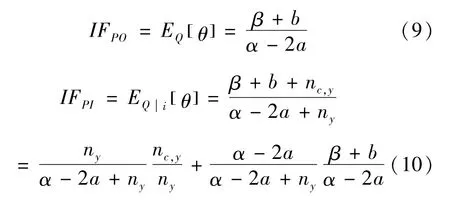
联立方程（1）、（9） 和（10），得后验影响因子IFPI：

联立方程（2）、（11）和（12），可得R-后验影响因子 RIFPI：

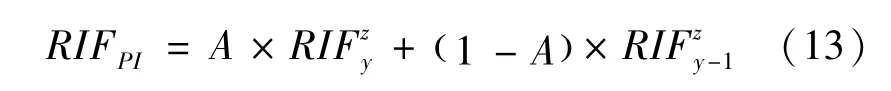
从公式（11）和（13）不难发现期刊后验影响因子IFPI和R-后验影响因子RIFPI是明显不同的。期刊后验影响因子IFPI只涉及期刊2年的JIF，而R-后验影响因子RIFPI包含两个元素：期刊影响因子JIF和描述期刊论文长期影响力的被引半衰期T0.5。

2 实证分析与讨论

为检验R-后验影响因子RIFPI在期刊评价中的效果，选取2012年6月汤森路透公司发布的2011年度期刊引证报告（JCR）中JIF≥3.0的物理学领域34种科技期刊为研究对象，并将它们按2011年影响因子值排列，结果如表1所示。

表1 34种物理类期刊各参量及名次变化对比情况

为了更好说明R-后验影响因子RIFPI在期刊评价中的作用，首先分析了基于贝叶斯理论的后验影响因子IFPI。从表1中不难发现，后验影响因子IFPI方程（11）反映出信息量（如，发文量）越大，与先验信息相比现在的JIF也越大。在这种条件下，对于那些刊载大量论文的高质量期刊，如Phys Rev B（n2011=6121， A=0.99578） 和 Appl Phys Lett（n2011=4419，A=0.97874），这种方法效果显著。

然而，还有一些期刊，尽管它们刊载的论文量足够大，但其可靠度因子却很低，如Classical Quant Grav（n2011=456，A=0.39117），出现这种状况的原因是在过去两年间的先验影响力具有很小的变量。由于此期刊在过去连续三年内的JIF几乎未发生显著变化（分别为3.32，3.098和 3.029），说明假定的先验影响力是正确的。

从表1第七列，还可以发现以后验影响因子IFPI大小进行排序时，名次降低的期刊（2种）和名次提高的期刊（3种）相差并不多，例如，Classical Quant Grav（A=0.39117）降低2名（从第29名降至31名）和Laser Phys（A=0.9912）名次降低1名（从第25名降至第26名）。名次提高的期刊分别是 Opt Express（A=0.98959）、Phys Rev C（A=0.93386） 和Comput Phys Commun （A=0.92139），均提高1名。以上期刊均表现出一种异常状态，它们在过去几年内JIF值起伏较大，后验影响因子IFPI在一定程度上能够消除这种陡变情况。

为了便于直观对IFPI和JIF进行比较，将它们进行作图（图1）。由于IFPI是一些离散点所组成，故对其进行线性拟合，拟合方程为IFPI=0.00729+0.9897×JIF，拟合表达式中常数项非常小，接近于零，而比例项接近于1，说明IFPI与JIF之间存在非常显著的线性关系，即IFPI既保留了JIF特性，又具独特的一面，能够部分消除期刊影响因子的突变情况。换句话也就是说那些JIF波动较大（即两年JIF相差的绝对值较大）的期刊相应偏离拟合曲线较远，可靠度也相应较小；可靠度较高期刊的偏离拟合曲线较近。如图中期刊Crit Rev Solid State偏离曲线较远，它的可靠度只有而其它期刊两种排序发生变化时，ΔJIF＜3，故没有以上两种期刊偏离程度之远。可靠度因子接近于1的期刊未发生显著变化，这主要是因研究的样本期刊均为JIF＞3.0的高质量期刊。

图1 IFPI随JIF相对变化情况

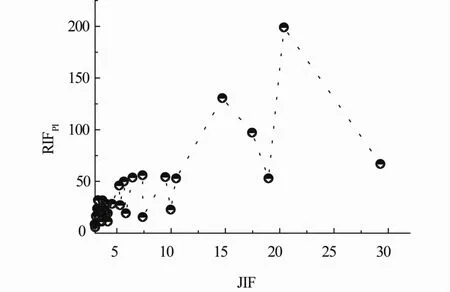
图2 34种JIF〉3.0物理学期刊RIFPI随JIF变化情况

最近，R-因子被用到研究影响因子操纵过程中影响因子和可靠性影响因子的变化过程，并发现可靠性影响因子可以部分抵消人为操纵行为的影响，说明R-因子对传统影响因子JIF有一定修正作用［14］。图2描述的是JIF≥3.0物理学期刊RIFPI与JIF的关联性，这与Kuo和Rupe等人研究IEEE的系列期刊时的R-因子变化情况相似［10］。这说明RIFPI与R-因子一样，都能对传统影响因子JIF具有一定的修正作用，其不但能用来描述期刊被引寿命，而且还能描述期刊中被发表的论文的被引率。RIFPI与R-因子不同之处在于RIFPI是建立在严格的统计理论基础之上的，并且具有可靠性因子A（表1第5列），而R-因子没有。从表格1最后一列还可以发现，除了最后一种期刊 Appl Phys Express的排序没有改变外，其它期刊的排序均已发生变化，这与按基于贝叶斯得到的后验影响因子IFPI排序大大不同，这主要是因为后验影响因子IFPI虽对影响因子JIF进行了修正，将研究年限从传统JIF的2年提高到后验影响因子IFPI的5年，但还是不能有效的控制影响期刊影响因子的因素（如操作行为）的发生，而只能在一定程度上减轻由于人为等因素带来的影响因子的增加。而R-后验影响因子RIFPI由于是在期刊影响因子基础上引入期刊被引半衰期，从而把长期的变化因素考虑进来，从而能够大大的消除那些影响期刊影响因子的因素所带来的影响，从提高对期刊评价度。［14］

3 结论

后验影响因子IFPI以贝叶斯统计理论为基础，其虽只考虑了相邻年份传统影响因子JIF的影响，但对JIF能起到一定的平滑作用，所以得到的结果相对JIF具有一定的客观性和稳定性；而R-后验影响因子RIFPI是在IFPI基础上引入期刊被引半衰期，从而把长期的变化因素考虑进来，进而能够大大消除人为因素对期刊影响因子的影响，对传统影响因子JIF起到较好的修正作用，提高期刊评价效果。因计算RIFPI所需的数据均可以直接从JCR中获得，计算过程简单且具有可操作性。此外，通过对34种JIF≥3.0的物理学领域期刊的实证研究，发现RIFPI与IFPI和JIF相比，不但能描述期刊被引寿命，而且还能描述期刊中论文的被引率。

1 Garfield E.Citation indexes for science：a new dimension in documentation through association of ideas.Science， 1955，122（3159）： 108-111

2 Garfield E.Citation analysis as a tool in journal evaluation.Science，1972，178 （4060）：471-479

3 Braun T.（Ed.） Special discussion issue on journal impact factors［Special issue］.Scientometrics， 2012， 92 （2）

4 Bagatin E， Gontijo B.The expansion of a measure： what is a scientific journal impact factor and how important is it for academic Brazilian dermatologists.International Journal of Dermatology，2011， 50（11）：1432-1434

5 Loet L.Alternatives to the journal impact factor：I3 and the top-10% （or top-25%？） of the most-highly cited papers.Scientometrics， 2012， 92（2）： 355-365

6 Brown T.Journal quality metrics：options to consider other than impact factors.the American Journal of Occupational Therapy，2011， 65（3）： 346-350

7 Gualberto B.&Izabela Z.What do the scientists think about the impact factor？.Scientometrics，2012， 92（2）： 281-292

8 Hirsch J.An index to quantify an individual's scientific research output.In：Proceedings of the National Academy of Sciences of the United States of America， 2005， 102（46）：16569-16572

9 Braun T，GlanzelW，Schubert A.A Hirsch-type index for journals.Scientometrics， 2006， 69（1）：169-173

10 KuoW and Rupe J.R-impact factor：Reliability-based citation impact factor.IEEE Transaction on Reliability， 2007， 56（3）： 366-367

11 Patricia P， JoséP.s， Antonio A.， et al.An annual JCR impact factor calculation based on Bayesian credibility formulas.Journal of Informetrics， 2013， 7（1）： 1-9

12 Morris C N.Natural exponential families with quadratic variance functions.Annals of Statistics， 1982， 10（1）： 65-80

13 Chen L， Eichenauer-Hermann J， Hofmann H.， et al.Gamma-minimax estimators in the exponential family［EB/OL］.［2013-1-08］.www.impan.pl/Preprints/p661.pdf

14 Guang Yu，Dong-Hui Yang and Wang Liang.Reliability-based citation impact factor and the manipulation of impact factor.Scientometrics，2010， 83（1）： 259-270