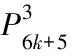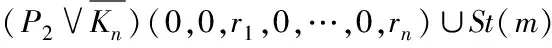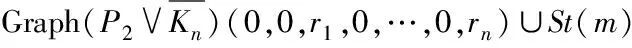非连通图C4m-1∪C12m-8∪G的优美标号
吴 跃 生
(华东交通大学 理学院, 江西 南昌 330013)
1 主要概念
本文所讨论的图均为无向简单图,V(G)和E(G)分别表示图G的顶点集和边集,记号[m,n]表示整数集合{m,m+1,…,n},其中,m和n均为非负整数,且满足0≤m 图的优美标号问题是组合数学中一个热门课题[1-11]. 本文讨论非连通图C4m-1∪C12m-8∪G的优美性. 定义1[1]对于一个图G=(V,E),如果存在一个单射θ:V(G)→[ 0, |E(G)|],使得对所有的边e=(u,v)∈E(G),由θ′(e)=|θ(u)-θ(v)|导出的E(G)→[1,|E(G)|]是一个双射,则称G是优美图,θ是G的一组优美标号,称θ′为G的边上的由θ导出的诱导值. 定义2[1]设f为G的一个优美标号,如果存在一个正整数k,使得对于任意的uv∈E(G),有 f(u)>k≥f(v) 或f(u)≤k 成立,则称f为G的平衡标号(或称G有平衡标号f),且称k为f的特征.图G称为平衡二分图(balanced bipartite graph). 显然,若f为G的平衡标号,则k是边导出标号为1的边的两个端点中标号较小的顶点的标号. 定义3[1]在平衡二分图G中,设其优美标号θ的特征为k,并且θ(u0)=k,θ(v0)=k+1,则称u0为G的二分点,v0为G的对偶二分点. 定义5[3-4]V(G)= {u1,u2,…,un}的每个顶点ui都粘接了ri条悬挂边(ri为自然数,i=1,2,…,n)所得到的图,称为图G的(r1,r2,…,rn)-冠,简记为G(r1,r2,…,rn). 特别地,当r1=r2=… =rn=r时,称为图G的r-冠.图G的0-冠就是图G. 定理对于任意正整数m,如果图G是特征为k且缺k+6m-3标号值的交错图(6m-3≤k+6m-3≤|E(G)|),那么非连通图C4m-1∪C12m-8∪G存在缺标号值k+1的优美标号. θ(x2i)=6m+i+k-2 (i=1,2,…,2m-1); θ(x2i-1)=10m-i+k-3 (i=1,2,…,m); θ(x2m+1)=3m+k; θ(x2i-1)=10m-i+k-2 (i=m+2,m+3,…,2m); θ(y2i-1)=16m-8-i+k(i=1,2,…,6m-5); θ(y12m-9)=k+22m-12; 下面证明θ是非连通图C4m-1∪C12m-8∪G的优美标号. (1)θ:X→[0,k]是单射(或双射); θ:Y→[k+16m-8,q+16m-9]-{k+22m-12}是单射(或双射); θ:V(C4m-1)→[k+6m-1,10m-4+k]∪{3m+k}是单射(或双射); θ:V(C12m-8)→[k+2,6m-2+k]∪[10m-3+k,16m-9+k]∪{22m-12+k}-{3m+k}是单射(或双射); θ:V(C4m-1∪C12m-8∪G)→[0,q+16m-9]-{k+1}是单射. θ′(x2m+2x2m+1)=4m-1; θ′(x2mx2m+1)=4m-2,θ′(x4m-1x1)=2m-2; θ′:E(C4m-1)→[1,4m-1]是双射; θ′(y12m-9y12m-8)=16m-10; θ′(y12m-10y12m-9)=16m-9,θ′(y12m-8y1)=10m-7; θ′:E(C12m-8)→[4m,12m-9]是双射; θ′:E(G)→[16m-8,q+16m-9]是双射; 由(1)和(2)可知θ就是非连通图C4m-1∪C12m-8∪G的缺k+1标号值的优美标号. 引理1 对于任意正整数n,设C4n是有4n个顶点的圈,则C4n存在特征为2n-1且缺3n的交错标号. 证明 记圈C4n上的顶点依次为v1,v2,…,v4n,定义圈C4n的顶点标号θ为 容易验证,θ就是圈C4n的特征为2n-1且缺3n的交错标号. 注意到3n=(2n-1)+n+1,由定理和引理1有如下结论. 推论1 对于任意正整数m,非连通图C4m-1∪C12m-8∪C24m-16存在缺标号值12m-8的优美标号. 例1 由推论1,非连通图C7∪C16∪C32存在缺标号值16的优美标号为 31,26,30,27,21,28,29,31; 38,17,37,18,36,19,35,20,34,22,33,23,32,24,47,25,38; 0,55,1,54,2,53,3,52,4,51,5,50,6,49,7,48,8,46,9,45,10,44,11,43,12,42,13,41,14,40,15,39,0. 引理2[3]对于任意正整数m和任意自然数r1,r2,…,rm,C4m(r1,0,r2,0,…,rm,0,…,0)存在特征为2m-1且缺3m的交错标号. 注意到3m=(2m-1)+m+1,由定理和引理2有如下结论. 推论2 对于任意正整数m和任意自然数r1,r2,…,r6m-4,非连通图C4m-1∪C12m-8∪C24m-16(r1,0,r2,0,…,r6m-4,0,0,…,0)存在缺标号值12m-8的优美标号. 例2 由推论2,非连通图C7∪C16∪C32(1,0,2,0,3,0,4,0,5,0,6,0,7,0,8,0,0,…,0)存在缺标号值16的优美标号为 31,26,30,27,21,28,29,31; 38,17,37,18,36,19,35,20,34,22,33,23,32,24,47,25,38; 0(91),90,1(89,88),87,2(86,85,84),83,3(82,81,80,79),78,4(77,76,75,74,73),72,5(71,70,69,68,67,66),65,6(64,63,62,61,60,59,58),57,7(56,55,54,53,52,51,50,49),48,8,46,9,45,10,44,11,43,12,42,13,41,14,40,15,39,0. 引理3[3]对于任意正整数m和任意自然数r,C4m(r,r,…,r)存在特征为2m(r+1)-1且缺3m(r+1)的交错标号. 注意到3m(r+1)=[2m(r+1)-1]+m(r+1)+1,由定理和引理3有如下结论. 推论3 对于任意正整数m,n和任意自然数r,当6m-4=n(r+1)时,非连通图C4m-1∪C12m-8∪C4n(r,r,…,r)存在缺2n(r+1)标号值的优美标号. 例3 由推论3给出的非连通图C7∪C16∪C16(1,1,…,1)缺标号值16的优美标号为 31,26,30,27,21,28,29,31; 38,17,37,18,36,19,35,20,34,22,33,23,32,24,47,25,38; 0(55),54(1),2(53),52(3),4(51),50(5),6(49),48(7),8(46),45(9),10(44),43(11),12(42),41(13),14(40), 39(15),0(55). 由推论3给出的非连通图C7∪C16∪C8(3,3,…,3)缺标号值16的优美标号为 31,26,30,27,21,28,29,31; 38,17,37,18,36,19,35,20,34,22,33,23,32,24,47,25,38; 0(55,54,53),52(1,2,3),4(51,50,49),48(5,6,7),8(46,45,44),43(9,10,11),12(42,41,40),39(13,14,15),0(55,54,53). 由推论3给出的非连通图C7∪C16∪C4(7,7,7,7)缺标号值16的优美标号为 31,26,30,27,21,28,29,31; 38,17,37,18,36,19,35,20,34,22,33,23,32,24,47,25,38; 0(55,54,53,52,51,50,49),48(1,2,3,4,5,6,7),8(46,45,44,43,42,41,40),39(9,10,11,12,13,14,15),0(55,54,53,52,51,50,49). 本文研究了非连通图C4m-1∪C12m-8∪G的优美标号,给出了非连通图C4m-1∪C12m-8∪G是优美图的一个充分条件,可为继续研究非连通图Cm1∪Cm2∪…∪Cmn∪G的优美性提供借鉴. 参考文献: [ 1 ]马克杰. 优美图[M]. 北京:北京大学出版社, 1991:1-247. (Ma Kejie. Graceful Graph[M]. Beijing: Beijing University Press, 1991:1-247.) [ 2 ]路线,潘伟,李秀芬. 图St(m)∪Kp,q的k优美性及算术性[J]. 吉林大学学报:理学版, 2004,42(3):333-336. (Lu Xian, Pan Wei, Li Xiufen.k-Gracefulness and Arithmetic of GraphSt(m) ∪Kp,q[J]. Journal of Jilin University: Science Edition, 2004,42(3):333-336.) [ 3 ]吴跃生. 关于圈C4h的(r1,r2,…,r4h)-冠的优美性[J]. 华东交通大学学报, 2011,28(1):77-80. (Wu Yuesheng. On the Gracefulness of the (r1,r2,…,r4h)-Corona of the CycleC4h[J]. Journal of East China Jiaotong University, 2011,28(1):77-80.) [ 4 ]吴跃生,李咏秋. 关于圈C4h+3的(r1,r2,…,r4h+3)-冠的优美性[J]. 吉首大学学报:自然科学版, 2011,32(6):1-4. (Wu Yuesheng, Li Yongqiu. On the Gracefulness of the (r1,r2,…,r4h+3)-Corona of the CycleC4h+3[J]. Journal of Jishou University: Natural Science Edition, 2011,32(6):1-4.) [ 7 ]吴跃生. 图C7(r1,r2,r3, ,r4,r5,0,0)∪St(m)的优美性[J]. 吉首大学学报:自然科学版, 2012,33(5):9-11. (Wu Yuesheng. on the Gracefulness of the GraphC7(r1,r2,r3,r4,r5,0,0)∪St(m)[J]. Journal of Jishou University: Natural Science Edition, 2012,33(5):9-11.) [ 8 ]吴跃生,王广富,徐保根. 关于C4h+1⊙K1的(Gr1,Gr2,…,Gr4h+1,Gr4h+2)-冠的优美性[J]. 山东大学学报:自然科学版, 2013,48(4):25-27. (Wu Yuesheng,Wang Guangfu, Xu Baogen. The Gracefulness of the (Gr1,Gr2,…,Gr4h+1,Gr4h+2)-Corona of the GraphC4h+1⊙K1[J]. Journal of Shandong University: Natural Science, 2013,48(4):25-27.) [ 9 ]吴跃生. 关于圈C4h+3的(Gr1,Gr2,…,Gr4h+3)-冠的优美性[J]. 吉首大学学报:自然科学版, 2013,34(4):4-9. (Wu Yuesheng. On the Gracefulness of the (Gr1,Gr2,…,Gr4h+3)-Corona of the GraphC4h+3[J]. Journal of Jishou University: Natural Science Edition, 2013,34(4):4-9.) [10]吴跃生,王广富,徐保根. 非连通图C2n+1∪Gn-1的优美性[J]. 华东交通大学学报, 2012,29(6):26-29. (Wu Yuesheng,Wang Guangfu,Xu Baogen. The Gracefu-lness of the Unconnected GraphC2n+1∪Gn-1[J]. Journal of East China Jiaotong University, 2012,29(6):26-29.) [11]Gallian J A. A Dynamic Survey of Graph Labeling[J]. The Electronic Journal of Combinatorics, 2002(5):1-106.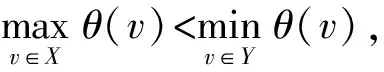
2 主要结果及其证明
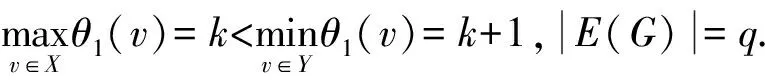
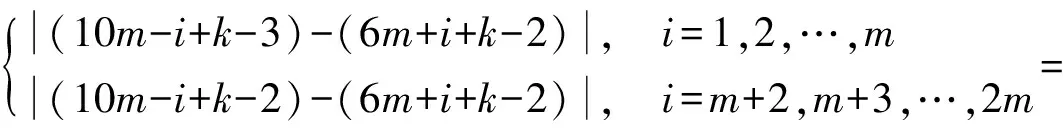
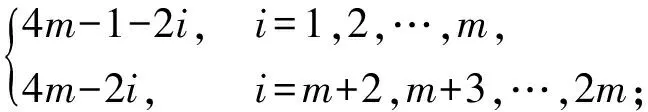


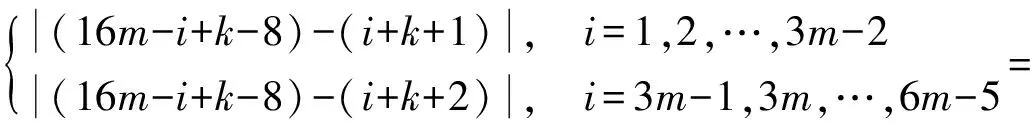

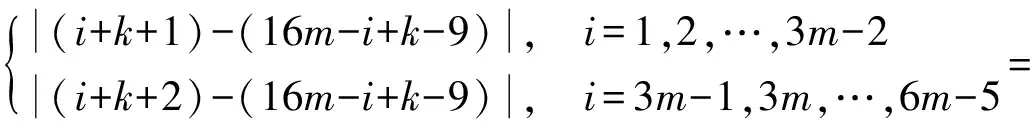

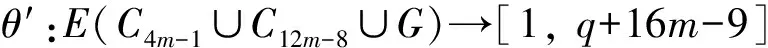
3 结 语