基于KPC-kNN方法的批次过程故障诊断

袁 杰， 郭小萍， 李 元

(沈阳化工大学 信息工程学院， 辽宁 沈阳 110142)

批次过程因其操作方便、附加值高等特点，被广泛应用到工业过程中.业内普遍认为通过对批次过程细节上的深入研究而更加深入地了解批次的运行状态，会促进生产力的进一步提升[1].但是批次过程灵活方便的操作特点也导致了复杂的数据特点，比如，批次过程数据的非线性关系、多操作工况、工时不等长、多时段、时段不等长等，这些特点导致批次过程的过程监控面临很多问题，如何处理批次过程的这些复杂特征成为热点.

针对批次过程的非线性处理，许多学者提出了不同方法.Nomikos和MacGregor提出了多向主元分析(MPCA)[2-3]，将PCA算法应用到充满复杂统计特征的批次数据中，由此衍生的基于PCA的很多算法也被提出来.但PCA方法不能全部提取出过程数据中的信息，因为PCA算法最初的应用领域是针对线性数据矩阵的.近年来，He Peter等提出一种基于近邻思维的kNN算法，这种算法并不在乎所处理的数据线性与否，但是在变量较多的情况下，该算法的计算量和存储量较大.使用PCA算法首先对原始数据进行降维，再进行kNN处理，即PC-kNN[4]，这种算法可有效减少计算量，然而，主元个数选择较少时，丢弃的原始信息有些多.近年来，核函数方法被广泛地应用于处理批次过程非线性问题.在这些核函数方法中，核主元分析因为其能迅速提取原始数据的非线性特征而(KPCA)应用最广.

本文结合KPCA和kNN的优点，提出一种KPC-kNN方法，使用核函数将原始的过程中有复杂非线性和耦合关系的低维数据映射到高维的线性空间中，在高维的线性空间中，使用PCA，将绝大部分信息提取出来，对这部分数据进行kNN处理.仿真实验验证了所提方法的有效性.

1 基于KPC-kNN的故障检测算法

1.1 核主元分析

作为非线性数据和线性数据之间的重要的联系，基于核思想的方法最早要追溯到20世纪20年代.在20世纪60年代后期，核方法首先被应用到模式识别中解决非线性问题.近年来，核方法逐渐受到人们的关注，很多基于核思想的新方法被提出.

核方法是对于一类非线性操作的总的称呼，这些方法的共同特点是都使用核函数将低维的非线性数据空间映射到高维的线性核空间中[5]，然后，在高维的线性空间中就可以应用各种其他检测算法，以此去除过程数据的非线性特点.通过核方法进行计算，去掉过程的非线性特点，计算可以更加精确.常用的核函数如下所示.

线性核函数：

K(x,xi)=x·xi

(1)

多项式核函数：

K(x,xi)=[x·xi+1]p

(2)

径向基核函数(RBF):

(3)

核主元分析定义：假设x1,x2,…,xM是训练数据，所以{xi}可以代表原始的输入空间.核主元分析的主要方法是使用某种映射函数将输入空间的低维非线性数据映射到高维线性空间中，即特征空间.在特征空间里就可以使用主元分析方法，因为PCA算法要求数据必须是线性关系的.假设相应的映射函数是Φ，通过这个核函数，输入空间的数据可以映射到特征空间F中，特征空间中的数据应当符合以下公式：

(4)

特征空间的协方差矩阵可以表示为：

(5)

特征空间的特征值和特征向量满足：

Cv=λv

(6)

然后

Φ(xv)·Cv=λ(Φ(xv)·v)

(7)

考虑到所有的特征向量是输入空间的线性组合Φ(x1),Φ(x2),…,Φ(xM),因此有：

(8)

然后

Φ(xw)Φ(xw)TΦ(xu))=

(9)

在(9)式中,v=1,2,…,M.定义一个M×M的数据矩阵K.

Kuv=Φ(xu)·Φ(xv)

(10)

因此公式 (9)可以简化为:

Mλα=Kα

(11)

求解公式(11),即可求得特征值和特征向量.

当公式 (4)不满足时,需要对Φ进行修正处理：

u=1,2,…,M.

(12)

核特征空间被修正为:

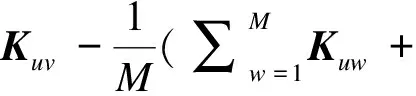
(13)

在这个特征矩阵中可以应用PCA算法,计算出T2和SPE并用来做检测指标.

1.2 k最近邻算法

kNN算法刚开始时被当做一种非参数的聚类方法来应用.k最近邻分类原则就是通过某个采样点的性质来预测其周围样本的性质.假如一个样本具有某种属性，那么其周围的样本也一定具有这样的性质.kNN方法用于故障检测的原理是：一个待检测的样本如果与训练样本的大部分数据离的比较近，那么它就是正常的，如果其远离了训练样本的主要聚集区，它很有可能是故障的样本.为了便于评价新来的待检测样本与建模样本的性质，kNN算法中使用标定的样本与其最近邻的k个样本之间的欧氏距离的平方和作为统计指标.算法的具体操作如下所示.

(1) 建模阶段

步骤1：对于所有用来建模的训练样本{X1，X2，…，XM},寻找与其相距最小的k个近邻样本，计算kNN平方距离，kNN的平方距离公式为：

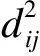
步骤2：当计算出所有样本的Ds之后，就可以通过核密度估计的方法求得这个Ds序列的累积分布函数，在设定置信区间的情况下，即得到该置信度下的控制限.

(2) 检测过程

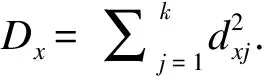
步骤2：将Dx与控制限Ds进行比较，如果Dx在控制限上方，则认为该样本是故障样本，反之，则认为该样本是正常样本.

1.3 KPC-kNN故障检测方法

对于上述两种算法，当变量个数特别多时，复杂的计算量不可避免.针对kNN 和 KPCA 算法的局限性，KPC-kNN可以在保证检测精度的同时，大幅度减少计算量.

(1) KPC-kNN的建模流程

步骤1：多批次过程数据按批次方向展开，并进行等长化处理，求取各列的均值和标准差.将建模数据进行标准化.

步骤2：标准化后的数据进行KPCA的操作，将数据映射到高维空间中，选择主元个数，并求取主元空间.

步骤3：在主元空间中使用kNN算法，结算每一个样本的Ds，将Ds序列使用核密度估计的方法求取控制限.

(2) KPC-kNN的检测流程

步骤1：新样本按批次方向展开，等长化处理，使用建模所得均值和标准差进行标准化操作.

步骤2：对新样本使用KPCA，得到在特征空间下的数据量.

步骤3：计算步骤2中数据量与建模样本的Dx，并与控制限做比较，确定是否为故障.

建模和检测的算法流程如图1所示.

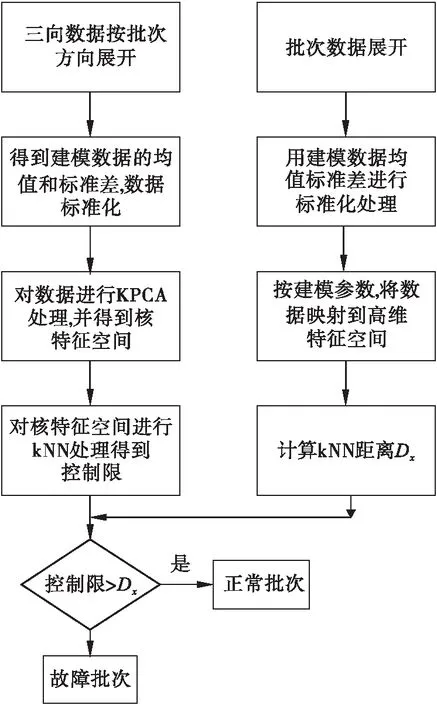
图1 KPC-kNN算法流程Fig.1 Flowchart of KPC-kNN method

2 批次过程仿真实例

使用半导体工业数据来说明所提算法的有效性.该工业过程的数据来源于在Lam 9600上进行的半导体铝蚀反应[4,6-7].包含108批次的正常数据和21批次的故障数据，因为有2个批次的数据存在大量丢失的情况，最后能用的建模数据是107批次，故障批次20批次.95批次正常数据用来建模、12批次的正常批次用来验证建模的准确性，最终要检测20批次的故障数据是否可以及时地被检测出来.

在应用该方法之前，需要对数据进行预处理.首先，从21个变量中选择出17个变量用来建模.使用最短长度法，将所有批次处理成85个采样时刻，并认为没有重要的信息遗失.最终所有批次数据成为(95×17×85)的三向矩阵，按批次方向展开所有批次的数据，如图2所示.所有85个采样时刻片(95×17)从三向数据中截取出来，并按顺序排列成为两向数据.

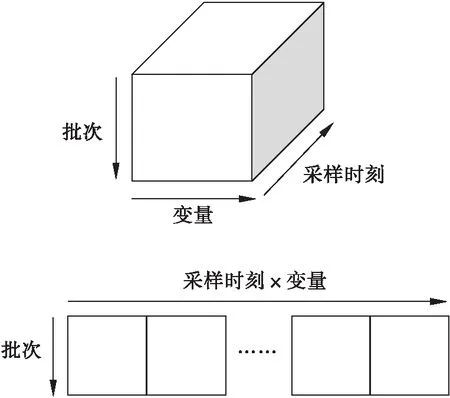
图2 批次过程3维数据展开方法Fig.2 Batch process 3-D data unfolded figure

在三向数据变为二向数据后，减去均值除以标准差对所有数据进行标准化操作.当数据完成标准化后，即可对这些数据应用各种算法.此处仅仅对比单纯使用KPCA、kNN以及KPC-kNN算法，实验结果如图3～图6所示.

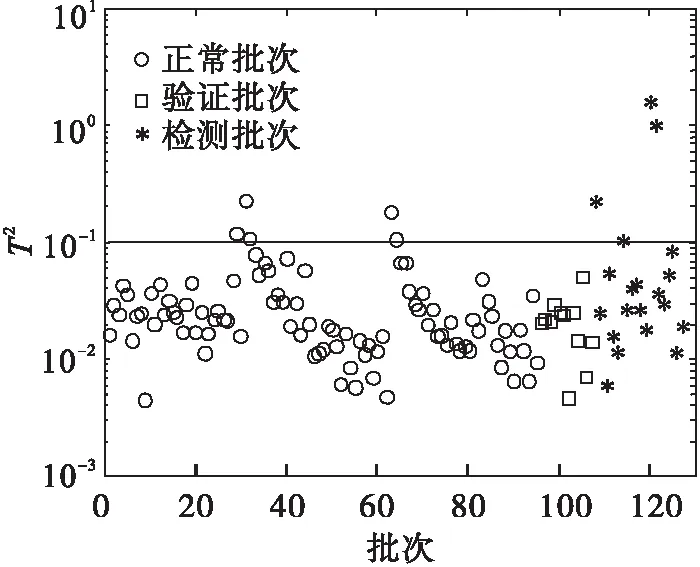
图3 KPCA的T2检测图Fig.3 Fault detection figure based on T2

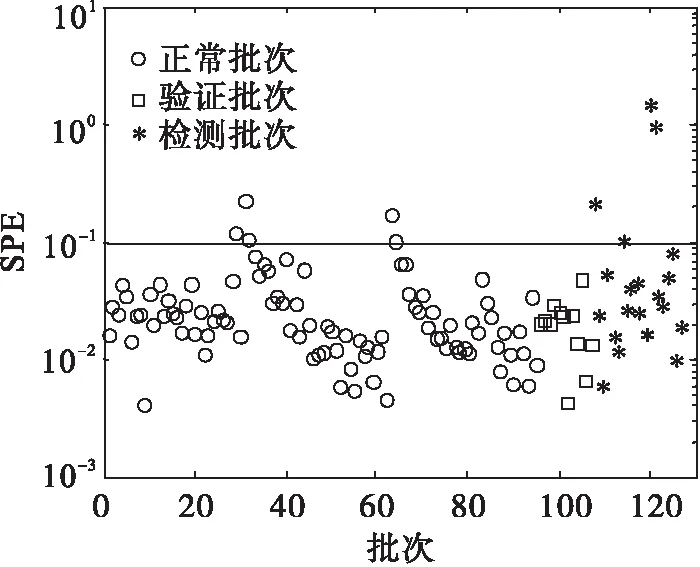
图4 KPCA的SPE检测图Fig.4 Fault detection figure based on SPE

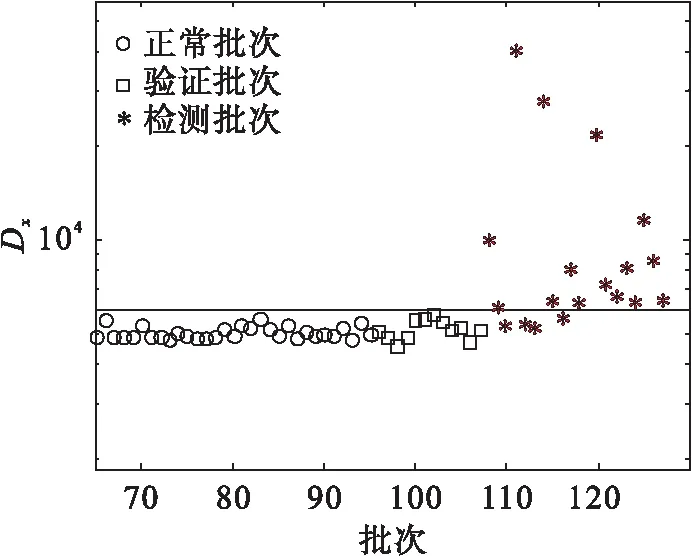
图5 kNN检测图Fig.5 Fault detection figure based on kNN

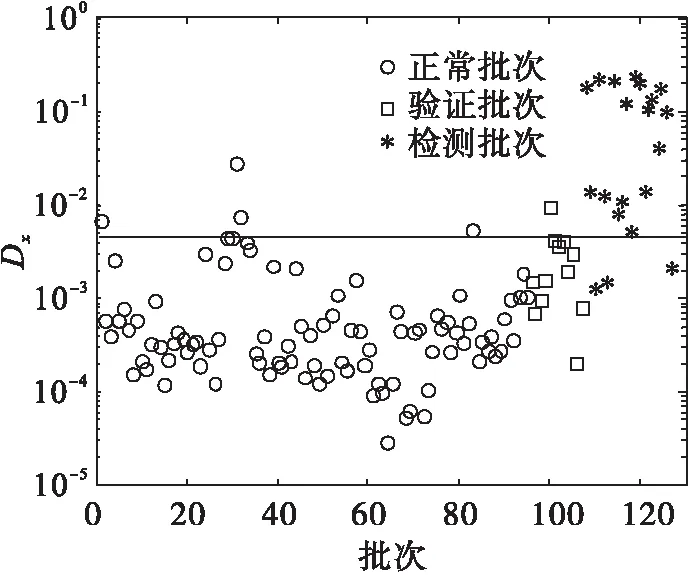
图6 KPC-kNN检测图Fig.6 Fault detection figure based on KPC-kNN

各种方法检测出的故障结果如表1所示.使用KPC-KNN算法，20 批次的故障可以检测出17批次，但是使用KNN算法，仅仅检测到16个批次的故障.根据数据提供的信息可知：4批没有检测出来的故障都是微弱故障.精度的提高是因为直接采用kNN算法操作时，有些重要性不强的变量变化干扰了过程的监控.而提取主元后的特征空间kNN则不会面对这个问题.然而，使用KPCA方法进行检测，两个统计指标交叉验证只检测到了6个批次故障.

表1 三种方法故障数目检测对比Table 1 The comparisons of different fault detection methods

3 结 论

结合kNN和KPCA各自的优点，提出一种KPC-kNN算法.在离线检测中，所提方法比单独使用kNN或KPCA都要好.实验结果验证了所提方法在故障检测中的良好效果.由于KPC-kNN算法提取建模数据非线性信息时使用了核函数，且核函数参数值方法目前仍为行业难题，一般是根据实验经验选取，所以这可能限制该方法的进一步推广

参考文献：

[1] 李元,谢植,周东华,等.MPCA在间歇反应过程故障诊断中的应用[J].化工自动化及仪表,2003,30(4):10-12.

[2] Nomikos P,MacGregor J F.Multivariate SPC Charts for Monitoring Batch Processes[J].Technometrics,1995,7(1):41-57.

[3] Nomikos P,MacGregor J F.Monitoring and Batch Processes Using Multi-way Principal Component Analysis[J].AlChE Journal,1994,40(8):1361-1375.

[4] He Q P,Wang J.Principal Component Based k-Nearest-Neighbor Rule for Semiconductor Process Fault Detection[C]// 2008 American Control Conference.Seattle,WA:IEEE,2008:1606-1611.

[5] Lee J M,Yoo C K,Choi S W,et al.Nonlinear Process Monitoring Using Kernel Principal Component Analysis[J].Chemical Engineering Science,2004,59(1):223-234.

[6] He Q P,Wang J.Fault Detection Using the k-Nearest Neighbor Rule for Semiconductor Manufacturing processes[J].IEEE Transactions on Semiconductor Manufacturing,2007,20(4):345-354.

[7] 郭小萍，袁杰，李元.基于特征空间k最近邻的批次过程监视[J].自动化学报,2014,40(1)：135-142.