基于备件分析的飞机最经济飞行强度选择

林 琳，王亮亮

（中国电子科学研究院，北京 100041）

引言

飞机的寿命周期费用是在飞机预期寿命内，采购、使用、维护（暂不考虑报废）所花费的费用之和[1]。在飞机设计阶段所做出的决策最有可能降低飞机的寿命周期费用，这时整个综合保障系统正在设计，且对飞机的设计易作出更改，而到了生产阶段做出的任何设计调整都要花费较大的成本。对于飞机来说，其寿命周期可以长达三十年，使用保障费用最终将大于采购飞机本身所用到的费用。从用户角度来看，采购费用是一次性的、可见的，而飞机的使用维护费用是预见的、未知的，因此在设计时确定的飞机最经济飞行强度十分必要。

飞机的使用维护成本主要包括使用过程中的各种充、填、加、挂造成的物资消耗和人力成本，以及维护维修过程中各种航材和人力的消耗。

因在飞机设计一定的情况下，飞机采购成本一定，本文基于备件分析来计算使用维护成本。将使用维护成本分为使用成本、材料成本以及人力成本，并将人力成本按照航材的成本进行折算。

目前，在计算使用维护成本时常忽略的问题有：

1）未包含寿命周期内定检的费用；

2）未包含有寿件更换的费用；

3）备件配置方案不尽合理，仅从单因素考虑可靠性对备件采购的影响来确定备件数量。

飞行小时的使用维护成本直接关系到用户对飞行的使用感受，同时也直接影响飞机的市场竞争力。本文针对不同类型的备件，利用针对性的方法计算出不同飞行强度下的使用维护成本，从而为最优飞行强度的选择提供决策依据。

1 单位飞行小时使用维护成本

飞机的飞行强度通常以年飞行小时来衡量，不同飞行强度下使用维护成本是不同的，为了找出飞行强度与使用维护成本之间的关系，在满足用户需求的前提下选择合理的飞行强度，以达到单位飞行小时下使用维护成本最为经济。

将飞机的使用维护成本细分为三部分：

使用维护成本=①材料成本+②人力成本+③使用成本

对于使用成本而言，主要考虑使用过程中的油料消耗和耗材消耗，油料消耗即燃油消耗，耗材消耗包括滑油、冷却液、液压油等的消耗。

对于人力成本主要分为日常使用的人力成本、日常维护的人力成本、排故的人力成本。日常使用的人力成本、日常维护的人力成本与飞行强度成正比，单机单位时间的日常使用和维护成本为常数。排故的人力成本，根据国内航空领域经验，排故过程中人力与备件（航材）的成本的比例大致为1:4，因此以备件（航材）成本为分析对象，人力成本取备件（航材）成本的25%。

对于材料成本，即航材成本，是整个使用维护成本的分析的关键。但航材的配置不尽合理，配备的长时间用不到，而没有配置的备件却常常发生短缺。从美军舰船备件使用率的情况来看，随舰配备的航材只有20%用到，而发生故障时却有近80%的航材无法得到满足。据美国空军2004年的统计数据，60%的停飞是由于用于直接维修的消耗件短缺造成的。因此本文先梳理了航材的种类，再根据各种不同种类航材的特点给出成本的计算方法。

2 航材（即备件）的种类

备件指在飞机全寿命周期内，为了保持和恢复系统的设计性能，并完成任务需求，所必需的备用组件、维修零备件等。按照装机件清单分析得到飞机的备件清单，具体流程如图1所示。

如图，备件主要分为随机备件、耗材、有寿件、初始及后续备件[2]：

1）随机备件

图1 备件确定的流程图

随机备件顾名思义即随飞机一同交付给用户的备件，散装件、消耗件、修理用零备件等通常考虑列为随机备件。随机备件清单根据RCMA和MTA结果或相似设备配套供应经验汇总各种散装件和消耗品供应数量得到。随机备件主要有：

①各种紧固件，如：螺钉、螺栓、螺帽、铆钉、卡锁、扣销等；

②各种轴承，如：滚动轴承、滚珠轴承等；

③各种防松件，如：圆锥、圆柱销和销轴等；

④各类密封件；各类保险丝和保安器，指示灯等；

⑤各种保险丝和保安器，指示灯等；

⑥各种修理用零备件：如碳刷等。

2）耗材

①各种润滑油（脂）和各类冷却液等；

②飞机轮胎；

③各类维护用品，如：液晶屏的清洗纱布和清洗剂等。

3）有寿件

有寿件，为预防性维修更换或报废期限的件及可以预计使用寿命的件，亦称限寿件。由RCMA分析得到的定期需更换，因此通常单独订货。

有寿件包括部分结构组件、部件和设备，如各种软管、灭火瓶、发电机轴承等。

4）初始及后续备件

初始备件及后续订货备件通常是指大的更换件（如部件、模件等），而机械结构、线缆和软件不包含在内，初始备件及后续订货备件有时也被称为备品。通过分析装机件中可以在外场直接更换的单元LRU、在内场可更换的单元SRU，得到LRU、SRU清单。通过备件数量的配置优化分析，在一定保障站点配备一定数量的LRU和SRU（其数量可以为0），即得初始备件、后续订货备件。

3 随机备件、耗材成本

随机备件，即各种消耗件，其每几年再次订货更新，需要量为当单架机年飞行小时除以再次订货的间隔，乘随机备件初始数量，再加上20%的安全余量。随机备件的成本PA如下式所示：

式中：T为单架机年飞行小时数，TP为再次订货间隔，QTYA为随机备件初始数量，PA为随机备件单价，LIFE为飞机寿命周期年。

耗材的费用确定需要计算每项耗材的消耗标准，消耗标准按照一次性使用的消耗器材每飞行100小时的消耗标准，据此确定耗材的年需要量，在订货时为了预防突发情况需增加20%的安全余量。消耗标准确定后每年依照统计情况对各项耗材的消耗标准进行确认。耗材使用维护费用PM如下式所示：

式中：T为单架机年飞行小时数，S为消耗标准，PM为耗材单价，LIFE为飞机寿命周期年。

4 有寿件成本

飞机的有寿件在其寿命周期内，有两种维护的方式，第一种是到寿命直接更换，比如软管等橡胶件、救生设备、灭火瓶等；另一种是在翻修期到达后对其进行翻修，经过一次或多次翻修后有寿件到达寿报废，更换新件，该种情况通常是一些较大的组件，如发动机、发电机等。

设有寿件成本总费用为PL，等于翻修总费用和更换总费用之和，若计算第一种情况的有寿件将翻修费用取零即可。

更换总费用=设备更换次数×飞机数量×单架机设备装机数量×备件采购费用

翻修总费用=设备翻修次数×飞机数量×单架机设备装机数量×单次翻修费用

因此费用计算主要取决于翻修次数和更换次数的计算，从载荷强度上有三种评判标准，分别为飞行小时（FH）、装机日历时间（TIME）和起落次数（CYC）。将装机日历时间、起落转换成在年飞行小时，比较取最小值即可。

设备更换次数=XX年飞行小时/min{FH更换、TIME更换、CYC更换}

设备翻修次数=XX年飞行小时/min{FH翻修、TIME翻修、CYC翻修}-设备更换次数

单次翻修费通常为采购费用的一定比例，参考国际翻修费用的统计，设定单次翻修费用为采购费用的30%。

举例某型交流发电机，该发电机每先到2200FH或6日历年或1300起落，需要返回承制厂更换轴承，翻修2次后报废。在年飞行强度为500FH时，日历时间6年（换算为500FH×6=3000FH），1300次起落（1300×3FH=3900FH，按每次飞行3小时），因2200FH<3000FH<3900FH，得2200FH飞行小时为判定标准，计算得30年飞机寿命周期内需2次更换、4次翻修。

按照以上方法计算可得有寿件的费用，例如年飞行强度500FH/Year、飞机总寿命30年有寿件的翻修次数和更换次数举例如表1和表2所示。其中，序号1的有寿件，不更换，需翻修7次；序号2的有寿件更换1次，翻修4次；序号3的有寿件，不更换，需翻修7次。在得到翻修次数、更换次数后，可求得有寿件的维护总费用。

5 初始备件和周转备件成本

初始备件配置设计方法应综合考虑备件可靠性和价格双方面的因素，在一定的费用的情况下达到最佳的系统可用度的配置。例如以多级备件优化模型为基础，应用边际优化原理进行的多级备件优化，在美军及北约军事组织广泛开展应用[3]。

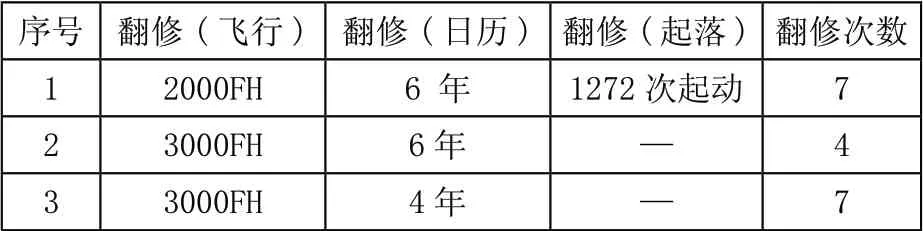
表1 有寿件翻修次数

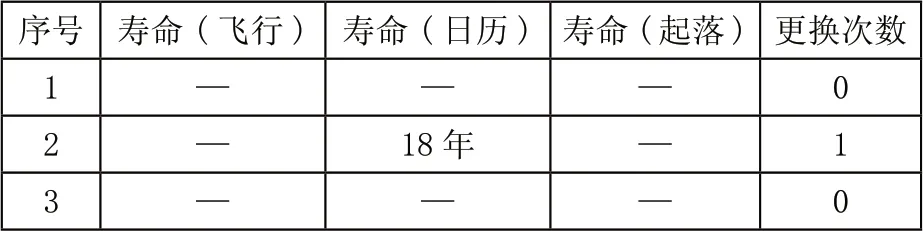
表2 有寿件更换次数

通过对算法进行改进，采用一种改进的分层边际优化算法，用以提高算法的优化效率。计算每年备件的需求率，即可得寿命周期内的备件采购费用。

设n为维修站点编号，i为初始周转备件编号，初始周转备件i在n站点需求率为λni[4]。

式中：NRTSnl为在维修站点n不能对可修复件i进行修复的比例；qnli为故障隔离率。

初始周转备件的需求率计算根据（3）式进行递推在基层级（O-level）进行，则LRUi在基层级（O-level）的年平均需求率，其中n∈Echelon(N)，i∈Inden(1)，则：

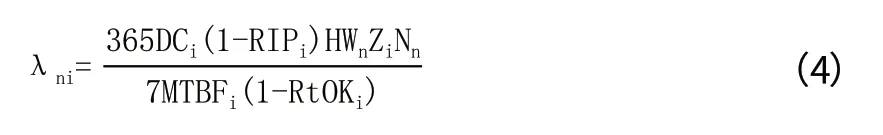
其中：DCi为占空比；RIPi为基层级（O-level）维修率；HWn为飞机的平均周飞行小时；Zi为初始周转备件i的装机数量；Nn为装备配置量；MTBFi为初始周转备件i的平均故障间隔时间；RtOKi为测试性的重测率。

6 案例

由4架飞机组成的机群部署在同一站点，在不同飞行强度下随机备件、耗材、有寿件、初始备件的费用情况如表3。

根据表3计算得单位飞行时间成本，可绘制单位飞行时间成本与飞行强度之间的关系图，即图2。如图可知，单位飞行时间成本成波浪型下降，而并非直线的线性下降。当年飞行强度为500FH时，单位飞行时间成本达到了最经济的成本5.15万元，而当飞行强度进一步增加时，单位飞行时间成本反而增加了。

导致这一现象的原因，主要有寿件的采购和翻修随着年飞行强度的增加有所变化而决定。当年飞行强度在300h/y时，由于发动机等大型有寿件在全寿命周期内需要多更换一次，并增加一次大修更换了大量有寿件，因此采购费用有了明显的增加，同样的情况在年飞行强度超过500h/y时发生。

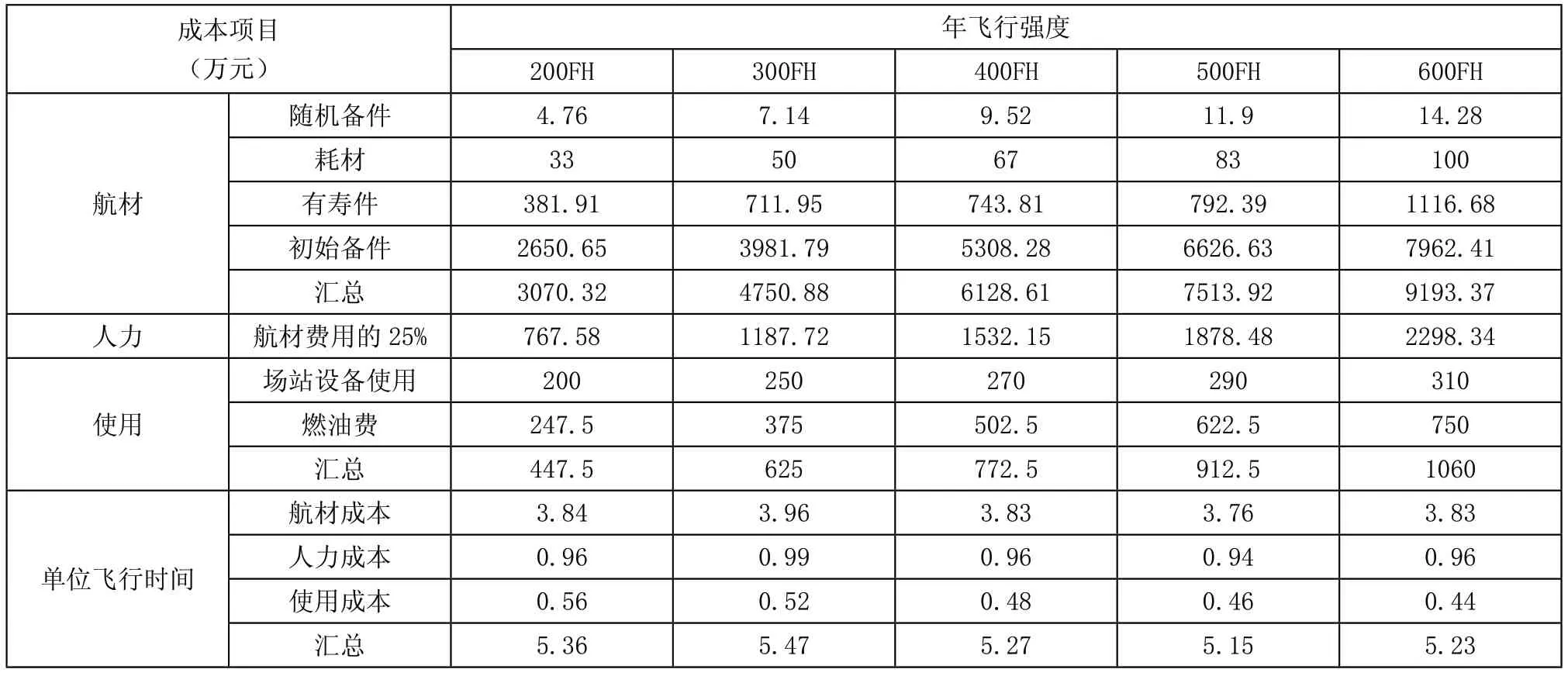
表3 飞机使用维护成本汇总表

图2 使用维护成本与飞行强度关系图

7 结论

本文通过将飞机的使用维护成本折算成航材成本，将不同航材类型进行了梳理，针对不同的航材成本提出的工程计算方法，并进行分别计算和分析，最终得到单位飞行小时的使用维护费用与年飞行强度的关系曲线，从而给出在设计可达的飞行强度区间段的最为经济合理的飞行强度。本文提出的方法，可用于设计阶段预先评估飞机的使用维护的成本，确定设计飞机的目标飞行强度。

[1]甘茂治,康建设,高崎,军用装备维修工程[M].北京：国防工业出版社,1999:197-206.

[2]GJB 4355-2002，备件供应规划要求[S].

[3]Sherbrooke C.C., VARI-METRIC: Improved Approximation for Multi-Indenture, Multi-Echelon Availability Models [M]. Operations Research,1986,34: 311-319.

[4]Sleptchenko A，van der Heijden M C，van Harten A．Effects of f inite repair capacity in multi-echelon，multi-indenture service part supply systems[J]．International Journal of Production Economics,2002,79:209-230．

[5]程海龙,康锐,龙军,康晓明,基于边际效应的备件保障率库存优化模型[J]. 兵工自动化,2008, 27(11):37-39,47.

[6]孙江生,李苏剑,吕艳梅,赵方庚,武器贵重备件三级库存模型方针研究[J]. 兵工学报,2008,29(07):854-858.