非惯性系之间相对运动方程的探讨
熊标, 郭振平
( 延边大学理学院 物理系, 吉林 延吉 133002 )
研究物体的运动规律时通常选取惯性参考系进行描述,但是当物体的运动情况比较复杂时,仅采用惯性参考系难以给出一个清晰且精确的描述,还要借助于一定的非惯性参考系[1-3].近年来,随着航天技术、空间探测技术和自动控制技术的高速发展,人们对机器人、航天器和卫星定位系统的精度要求越来越高,迫切需要研究非惯性系之间的相对运动问题[4-6].Alessi等人[7]从一个低地球轨道研究了地球-月球非惯性系统的特性;文献[8]基于太阳-地球-月球间的非惯性系统开发了一种用于载人航天任务的训练系统;Alipour等人[9]建立了非惯性系统动力学模型,并研究了悬浮的轮式移动机器人的稳定运动问题;Stephan等人[10]则根据非惯性系统动力学模型提出了全球定位的测距方程;姜雪洁[11]研究了地球表面附近相对运动的偏差;王正昌[12]根据加速度的相对性对伽利略变换进行了推广;梁立孚等人[13]提出了在非惯性系中研究动力刚化问题;赵培茈和郭振平[14]研究了非惯性系下的双滑轮运动的特性,指出了常见的分析误区.基于上述文献研究,本文为进一步研究两个转动非惯性系之间的相对运动规律,将惯性系与非惯性系之间的相对运动方程推广到非惯性系之间,通过非惯性系之间相对运动的分析建立了非惯性系之间的相对运动方程,并推导出非惯性系之间相对运动的速度和加速度的变换关系,进而讨论了以地球作为惯性参考系来计算转动速度和加速度是否合适.
1 转动非惯性系与惯性系之间的运动关系
如图1所示:在静止参考系S上建立坐标系O-xyz, 运动参考系S′以角速度ω′绕z轴逆时针转动;在运动参考系S′上建立坐标系O-x′y′z(两坐标系的原点及z轴重合).在静止参考系S中任一点P的位矢r与Ox′的夹角为γ1,Ox′与Ox的夹角为φ1, 则r投影到S′系为
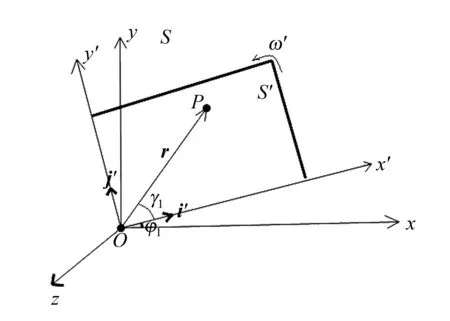
图1 动参考系相对静止参考系旋转
r=x′i′+y′j′,
(1)
而
(2)
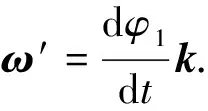
v=v′+ω′×r′.
(3)
2 两个转动非惯性系之间的速度关系
为消去(3)式中的v和ω′, 本文再引进一个以角速度ω″绕z轴逆时针转动的动系S″.在转动参考系S″上建立坐标系O-x″y″z, 使r与Ox″的夹角为γ2,Ox″与Ox的夹角为φ2(图2),则r投影到动系S″为r=x″i″+y″j″.
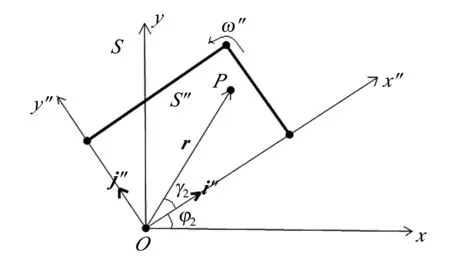
图2 转动参考系与静止参考系间的关系
同理可以求得
(4)
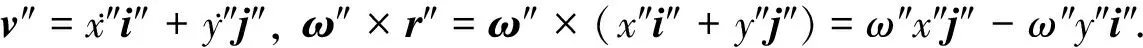
v′+ω′×r′=v″+ω″×r″.
(5)
不难证明r′=x′i′+y′j′=r″=x″i″+y″j″, 然后将r′=r″代入(5)式得
v′=v″+(ω″-ω′)×r″.
(6)
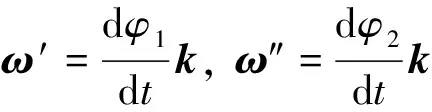
(7)
令θ=φ2-φ1, 将其代入(7)式得
(8)
将(8)式代入(6)式得
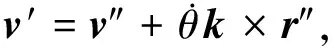
(9)
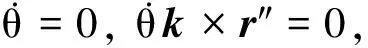
3 两个转动非惯性系之间的加速度关系
为了求加速度间的关系,将(3)式两端同时对时间t求导,得加速度a投影到S′系为
(10)
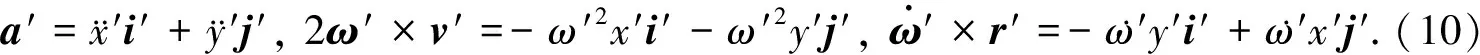
(11)
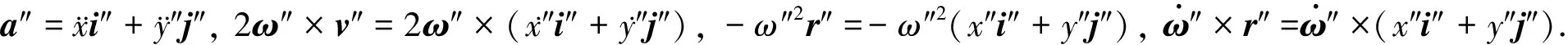
(12)
由(8)式可得
(13)
(14)
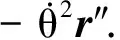
a向=-(ω″2-ω′2)r″.
(15)
4 结论
本文通过两个转动参考系间相对运动的分析,研究了两个非惯性参考系之间的运动关系,推导出非惯性系之间相对运动的速度和加速度表达式,并给出了以地球为非惯性参考系的向心加速度公式.本文研究表明,对于相对运动的运动学方程,在由一重非惯性系(由一个惯性系和一个非惯性系构成)向二重非惯性系(由两个非惯性系构成)推广的过程中,对于平面转动参考系,只有速度公式能用于二重非惯性系中,而加速度公式不再适用.因此,以地球为惯性系建立的相对运动方程,只有速度方程可用,而加速度方程必须进行修正.本文研究仅涉及宏观低速范围,关于高速条件下的相对论效应将另文讨论.
参考文献:
[1] Minguzzi E. The Minkowski metric in non-inertial observer radar coordinates[J]. American Journal of Physics, 2005,73(12):1117-1121.
[2] Baranyi L. Lift and drag evaluation in translating and rotating non-inertial systems[J]. Journal of Fluids & Structures, 2005,20(1):25-34.
[3] Poludnenko A Y, Khokhlov A M. Computation of fluid flows in non-inertial contracting, expanding, and rotating reference frames[J]. Journal of Computational Physics, 2007,220(2):678-711.
[4] Taheri B, Richer E. Equidistance target-following controller for under actuated autonomous underwater vehicles[J]. International Journal of Intelligent Computing and Cybernetics, 2013,6(2):108-125.
[5] Jayaram S. Fault tolerant autonomous rendezvous and docking architecture for spacecraft in presence of control actuator failures[J]. International Journal of Intelligent Unmanned Systems, 2013,1(1):5-20.
[6] Chahl J. Three biomimetic flight control sensors[J]. International Journal of Intelligent Unmanned Systems, 2014,2(1):27-39.
[7] Alessi E M, Gómez G, Masdemont J J. Two-manoeuvres transfers between LEOs and Lissajous orbits in the Earth-Moon system[J]. Advances in Space Research, 2010,45(10):1276-1291.
[8] Renk F, Hechler M, Messerschmid E. Exploration missions in the Sun-Earth-Moon system: a detailed view on selected transfer problems[J]. Acta Astronautica, 2010,67(1/2):82-96.
[9] Alipour K, Moosavian A. How to ensure stable motion of suspended wheeled mobile robots[J]. Industrial Robot, 2011,38(2):139-152.
[10] Stephan J G G. One-way light speed determination using the range measurement equation of the GPS[J]. Applied Physics Research, 2011,3(1):110-114.
[11] 姜雪洁.地表附近相对运动偏差研究[J].延边大学学报:自然科学版,2002,28(4):257-260.
[12] 王正昌.据加速度的相对性事实对伽利略变换进行推广[J].云南民族大学学报:自然科学版,2007,12(4):321-323.
[13] 梁立孚,王鹏,宋海燕.在非惯性系中研究动力刚化问题[J].哈尔滨工程大学学报,2012,33(8):1052-1056.
[14] 赵培茈,郭振平.双滑轮运动分析的常见误区[J].延边大学学报:自然科学版,2013,39(1):21-23.

