混合非结构网格下壁面最短距离的快速计算方法

王刚, 曾铮, 叶正寅

(西北工业大学 航空学院流体力学系, 陕西 西安 710072)

在高雷诺数流动问题的数值模拟中，通常需要在雷诺平均N-S方程中引入湍流模型来刻画湍流的脉动效应。目前常用的湍流模型包括一方程S-A模型及二方程(k-ε模型，k-ω模型等)及多方程模型(雷诺应力模型等)[1]。上述的湍流模型均需要利用壁面距离作为背景参数。对于结构网格而言，由于网格拓扑结构的规律性，其壁面距离的计算效率比较容易保证，而非结构网格舍去了网格连接的结构性和正交性限制，其拓扑结构具有很大的随意性，导致壁面距离参数的确定比较复杂。目前非结构网格中普遍采用的壁面距离计算方法是枚举法，即依次计算比较空间每个单元到所有表面单元的距离，这种算法精度足够但效率很低。因此，有必要研究适合非结构网格的高效、快速的壁面距离搜索算法。国内外对点到曲面最短距离的求法有很多文献资料，但大部分均是在曲面方程已知的情况下求解的[2-4]。如果采用这些方法，就需要重新分块拟合曲面方程，这需要耗费额外的工作量，不适用于计算流体力学中的离散曲面问题。而N.E.Renato等人提出的快速推进算法[5]，是针对非结构网格下的基于有限元方法求解距离函数的优化算法，其提升效率不错，但这种方法需要控制的变量太多，且其边界处理并不理想。T.Maruto等人采用的面集法[6]也是利用局部化的思想，将计算域限制在精确值附近的一个小区域内，提高计算的效率。但是这种算法需要单独考虑复杂边界的处理，在边界处常常会出现意想不到的问题。为了提高非结构网格中壁面距离搜索算法的效率，本文提出一种壁面逐层推进法。该算法只需计算流场中任意一个网格单元到目标面元(最短距离面元)及与其相邻的几个面元的距离即可，不需像枚举法一样计算到所有面元的距离，其算法复杂度比前述各类方法要低很多，且精度完全满足流场求解的要求，是一种理想的局部寻优算法。

1 壁面逐层推进法

1.1 算法原理

对于一个给定的已经离散化的表面，令S={S1,S2,…,Sm}代表该表面集合，其中Si代表壁面上的第i个面元。流场中任意一点用p=(xp,yp,zp)表示令qi(xq,yq,zq)为Si上距离p最近的一点，则最短距离函数为

(1)

当m→∞时，d可视为连续。在实际应用中，取qi为Si面心，p为流场某一网格单元的中心。当m充分多的情况下，距离函数d可近似为连续。

图1 逐层推进法原理示意图

将上述连续性假设应用到图1a)所示情形，第一层单元是表面网格单元层，Si(i=1,2,3,4,5)是表面单元编号。我们取B网格来观察，根据距离函数的连续性，与B网格最近的固壁面元信息应当来自于A、C、D3个网格单元。假设A、C、D各自存储的最近面元编号分别为S3、S2、S4，则B的最近面元应是这3个面元中到B距离最近的一个。

逐层推进法的另一个主要思想是将网格分层，从壁面单元层开始，向外逐层推进搜索计算。在没有明显分层结构的非结构网格中，首先设置2个数组RS和RS1，前者用来存储当前层的网格信息，后者存储下一层的网格信息，网格信息中增加一个“染色”标记FLAG用来标记该单元是否已经存储了最短距离，并以此来寻找下一层的网格。只要RS中的单元全部被染色，则所有RS中单元未被染色的邻居就视作空间的下一层。如图1b)，第1层全被染色后(灰色单元)，找到所有它们的未染色邻居(斜线单元)，视作第2层。该层染色后，标有数字的网格单元视作第3层，依此类推。 当整个空间网格中每一个单元都被染色，程序结束。

逐层推进法将连续性假设与分层思想结合起来，在图1a)中，第1层为表面网格单元层，很容易确定它们的格心分别到自身所含的壁面单元最近。对于第2层的B网格，它作为第1层A网格的未染色邻居被找到，计算它到S3的距离并将该距离及S3存入B的信息体，再计算它的所有邻居到S3的距离，分别存入各自对应的信息体中。当C网格作为第1层E网格的未染色邻居被找到时，同样进行如上操作，B网格作为它的邻居计算了到S2的距离，如果该距离小于之前存储的距离，则更新B的信息体。当一层全部计算完毕后将它们染色，继续下一层的计算，直到空间所有网格均被染色。

1.2 搜索算法的进一步改进

在实际应用中如果遇到很复杂的拓扑结构，前述算法可能会出现由于网格疏密不同而造成的反向推进。考察如图2所示的增升装置构型的计算网格进行距离计算结果，很容易看出图2a)的计算结果有误。出现该问题的原因是网格的疏密不同造成了逐层推进时信息传递出现了错误。被深色“吃掉”的区域由于该处表面网格密集导致推进速度远慢于两侧，当两侧推进到较远时，本属于密集区域的网格单元会作为稀疏区域单元的未染色邻居被找到，此时密集区域内层的单元尚未被染色，因而被认作了是外层单元的下一层。最后，密集区域的正反2种推进方式会在某一处相遇，形成一个交汇边界，在交汇边界的内侧，其所存距离是正确的，而外侧所存距离则是错误的，因为外侧网格的最近表面被认为来自物面的稀疏区域，如图3a)所示。

图2 未改进的算法可能遇到的问题示意图

图3 问题原因及解决方式

从壁面1向外推进，浅色单元表示储存了正确的面元，即壁面1，深色单元储存的是错误的面元，即壁面2。交汇时发生图3b)所示情形，算法停止。

本文对前述算法进行了改进。解决方法是在交汇边界处计算邻居单元的距离时，若发现所存距离需要更新但该单元已被染色，此时需要将该单元的FLAG重新置为FALSE，即去除染色，使推进过程可以重新由近场向远场进行。如图3c)，深色单元被依次去除染色，程序可以继续进行。正反两种推进方式还可能发生图3d)所示的交汇情形，处理方法是一样的。

2 算例分析

以类空天飞机外形[7]、三维增升装置[8]及DLRF6翼身组合体[9]的计算网格为考察对象，将逐层推进法的壁面距离计算结果与枚举法比较，测试算法的精度，并考察逐层推进法的计算结果在整个流场空间的平均相对误差以及最大相对误差。令

(2)

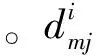
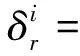
(3)

平均相对误差

(4)

最大相对误差

(5)

利用逐层推进法的壁面距离计算结果，对上述外形的黏性流场进行RANS方程求解计算，计算采用的求解算法参见文献[10]。通过流场计算结果(截面Cp分布)与实验值的比较，验证逐层推进法计算的壁面距离在流场计算中的有效性。

2.1 类空天飞机模形

本例的类空天飞机模型采用混合非结构网格，网格单元总数为1 845 705个，表面网格总数为61 442个。其流场计算状态为马赫数4.94，雷诺数5.26×107，迎角为0°，采用的湍流模型是S-A一方程模型。表1给出了最短物面距离的计算时间比较结果。

在本例中枚举法采用的是八核并行的运行机制，而逐层推进法采用单核计算。由表1可知，枚举法的计算时间为逐层推进法的58倍。如果单纯考虑实际计算量，逐层推进法的计算效率约为枚举法的464倍。

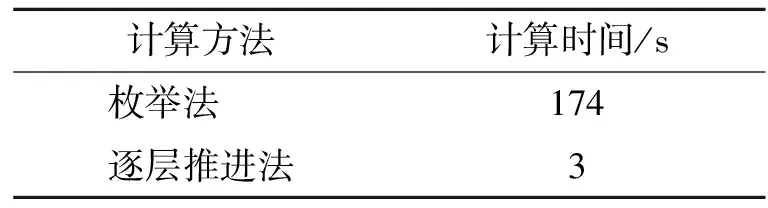
表1 2种算法计算时间比较(空天飞机)

图4 空天飞机模型网格切片图 图5 空天飞机壁面距离等值线图

图4给出的是机体某铅垂截面的网格切片图，图5给出该截面计算所得的壁面距离等值线图。图中枚举法的等值线设为虚线，逐层推进法的等值线设为实线，实线和虚线吻合，说明距离计算结果精度较好。新算法在整个流场中的平均相对误差δave=8.257×10-5，最大相对误差δmax=0.019，相对误差在各区间的分布如表2所示。

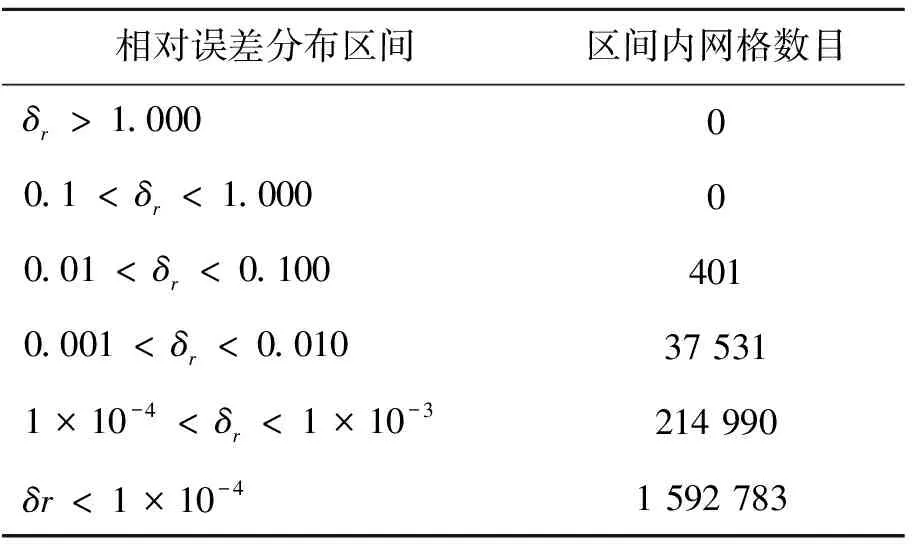
表2 类空天飞机模型壁面距离相对误差分布范围

虽然表2中有少数的网格其壁面距离的相对误差在1%到10%之间，但其在总网格中所占的比例极小，且位置均在附面层外，因此对流场计算结果不产生实质性影响。图6给出了子午线截面处Cp的计算值与实验值对比。图中计算值与实验值符合良好，进一步证明逐层扩散法计算得到的壁面距离具备有效的精度，可以适用于本算例的高超声速流场计算。

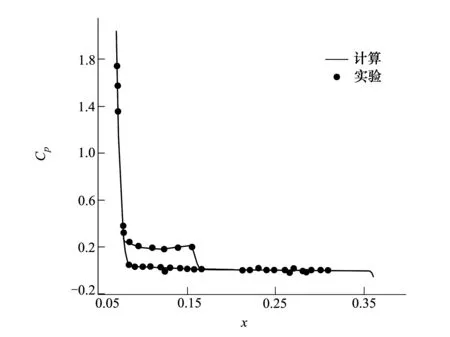
图6 子午线截面处Cp计算值与实验值对比图

2.2 增升装置模形

该模型采用结构化网格，共有5 957 632个网格单元，表面有65 248个单元。其流场计算状态为马赫数0.2，雷诺数4.3×106，迎角为13°。计算采用S-A一方程湍流模型。2种算法的最短物面距离计算时间如表3所示。

表3 2种算法计算时间比较(增升装置)

由表3可知，枚举法的计算时间为逐层推进法的65.7倍，实际计算量枚举法约为逐层推进法的525.6倍。本算例由于和类空天飞机模型的表面网格数目大致相当，因此效率提高倍数也基本相同。

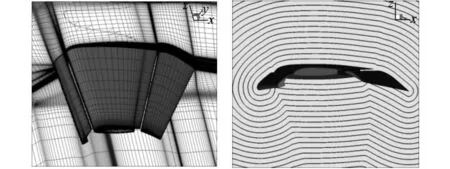
图7 增升装置模型网格切片图 图8 增升装置壁面距离等值线图

7给出了增升装置模型机翼某铅垂截面的网格切片图，这是一个结构化网格。图8是该截面距离等值线示意图。由图可见，等值线分布均匀，与枚举法吻合良好，说明逐层扩散法在此算例中计算精度较好。以枚举法的结果作为标准，其中整个流场平均相对误差δave=8.25×10-7，最大相对误差δmax=0.119。相对误差在各区间的分布列表如下：

表4 增生装置模型壁面距离相对误差分布范围

由表4可得，绝大部分网格的相对误差分布在一个极小的范围内。将逐层扩散法计算所得的壁面距离引入流场求解中，图9给出了翼展方向50%处的截面Cp的计算值与实验值对比，结果显示计算值与实验值吻合良好。该算例的流场结果表明，逐层扩散法计算的壁面距离同样可以良好适用于结构化网格。

图9 增升装置翼展50%截面Cp计算值与实验值对比

2.3 DLR-F6翼身组合体模型

该模型来自第二届AIAA 阻力预测会议，本文测试的是非结构混合网格，其网格单元总数为13 641 688个，表面网格单元有250 245个。流场计算状态为马赫数0.75，雷诺数3.0×106，迎角为1°，采用MSST两方程模型。两种算法的最短物面距离计算时间如表5所示：

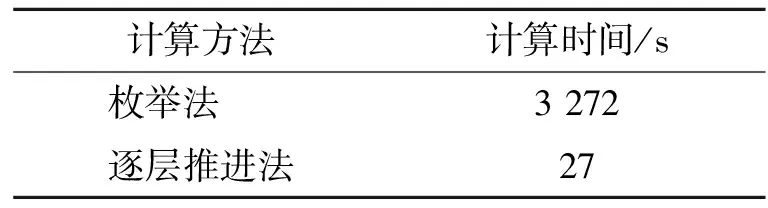
表5 2种算法计算时间比较(DLR-F6)

由表5知,对于本例中表面网格数量达到25万的大型网格，枚举法的计算时间为逐层推进法的121倍，实际计算量为逐层推进法的968倍，可见所提算法在壁面网格数目很大的情况下相比枚举法更具优越性。

图10 DLR-F6模型网格切片图 图11 DLR-F6模型距离等值线图

图10和图11分别给出了通过发动机轴线的铅垂截面的网格切片和距离等值线示意图。逐层扩散法计算的壁面距离等值线在壁面外围呈均匀分布，与枚举法吻合良好，证实逐层扩散法计算的壁面距离在此算例中精度较好。以枚举法的结果作为标准，其中整个流场平均相对误差δave=2.129 812×10-4，最大相对误差δmax=0.311 541。相对误差在各区间的分布列表如下：

表6 DLR-F6模型壁面距离相对误差分布范围

由表6可见，壁面距离的相对误差在1%以上相比起前2个算例增多，但网格单元总数是前2个算例的2倍以上，相对误差较大的单元占网格单元总数的比例并未变大。图12给出了翼展方向37.7%的截面Cp的计算值与实验值对比，由图可见计算值和实验值吻合良好。该算例流场计算结果表明，对于大型复杂非结构网格，逐层扩散法计算的壁面距离精度较好，具有良好的适应性。

3 结 论

本文提出了一种计算流场网格单元到壁面最短距离的逐层推进算法，并给出了该算法的原理和求解过程。该算法主要针对非结构网格由于拓扑结构的随意性导致壁面距离求解困难的问题。通过3个典型算例对本文提出的壁面最短距离逐层推进算法进行了考察和验证计算。结果表明，本文算法可有效处理任意复杂的边界，既可用于非结构网格的计算，也适用于结构网格，具有很好的普适性。该算法较枚举法的计算效率高2～3个量级，精度完全满足湍流模型的求解要求。随着壁面复杂程度的提升，该算法相比起枚举法的优越性会愈发明显。

参考文献：

[1] David C W. Turbulence Modeling for CFD[M]. 2nd Edition. DCW Industries, 2000:30-39

[2] 徐汝锋，陈志同，陈五一. 计算点到曲面最短距离的网格法[J]. 计算机集成制造系统, 2011, 17(1): 95-100

Xu Rufeng, Chen Zhitong, Chen Wuyi. Grid Algorithm for Calculating the Shortest Distance from Spatial Point to Free-Form Surface[J]. Computer Integrated Manufacturing Systems, 2011, 17(1): 95-100 (in Chinese)

[3] 苏智剑，吴序堂，毛世民.遗传算法在求解空间曲线与曲面间最短距离中的应用[J].机械设计与制造，2003(6):56-57

Su Zhijian, Wu Xutang, Mao Shimin. Genetic Algorithms for Solving the Minimum Distance between Bezier Curves and Surfaces[J]. Machinery Design and Manufacture, 2003(6): 56-57 (in Chinese)

[4] 陈丽萍，陈燕，胡德金.一种快速完备的自由曲线和曲面间最短距离求取算法[J]. 上海交通大学学报，2003,37(Suppl 2)：41-44

Chen Liping, Chen Yan, Hu Dejin. A High-Efficiency Algorithm to Calculate the Shortest Distance between Free-Form Curve and Free-Form Surface[J]. Journal of Shanghai Jiaotong University, 2003,37(Suppl 2)：41-44 (in Chinese)

[5] Renato N E, Marcos A D, Alvaro L G. Simple Finite Element-Based Computation of Distance Functions in Unstructured Grids[J]. Int J Numer Meth Engng, 2007, 72: 1095-1110

[6] Mauro T, David A S. Calculating Particle-to-Wall Distances in Unstructured Computational Fluid Dynamic Models[J]. Applied Mathematical Modelling, 2001, 25: 803-814

[7] 李素循. 典型外形高超声速流动特性[M]. 北京：国防工业出版社， 2007

Li Suxun. Hypersonic Flow Characteristics of Typical Appearance[M]. Beijing: National Defense Industry Press, 2007 (in Chinese)

[8] Rumsey C L, Slotnick J P, Long M. Summary of the First AIAA CFD High-Lift Prediction Workshop[J]. Journal of Aircraft, 2011,48(6):2068-2079

[9] Hemsch M J, Morrison J H. Statistical Analysis of CFD Solutions from 2nd Drag Prediction Workshop[R]. AIAA-2004-556

[10] 王刚，叶正寅.三维非结构混合网格生成与N-S方程求解[J]. 航空学报，2003,24(5)：385-390

Wang Gang, Ye Zhenyin. Generation of Three Dimensional Mixed and Unstructured Grids and Its Application in Solving Navier Stokes Equations[J]. Acta Aeronautica et Astronautica Sinica, 2003,24(5)：385-390 (in Chinese)