一种基于稀疏分解的微多普勒频率估计算法

金 斌，贾舒宜

（1.海军装备部兵器部，北京100073；2.海军航空工程学院电子信息工程系，山东烟台264001）

微多普勒的概念最初源于相干激光雷达系统[1]，这是由于激光雷达波长短（μm 量级），对目标小幅度运动非常敏感，具有很高的测速精度。美国海军研究实验室Chen V C 最早研究了雷达目标微动和微多普勒的现象，并在2000年引入微多普勒概念[2]，指出目标在相对雷达径向运动的同时，目标本身或其上的结构还存在着机械振动或旋转，将对雷达回波产生以目标平动多普勒为中心的边带多普勒调制，这种多普勒调制称为微多普勒效应(micro Doppler effect)，在目标多普勒频率上产生的边带频率称为微多普勒频率。微多普勒效应容易被S 波段、C 波段和X 波段等较高工作频率的微波雷达所感知。

Chen V C 最早指出雷达中也能够观测到微多普勒现象，并在文献[3]采用时频分析工具研究雷达目标的微动和微多普勒。目标微动状态常常是独一无二的，反映了目标的精细特征，可以用来作为目标识别的重要依据，在目标探测与识别领域的军事价值日益凸显，对空间、空中、地面目标识别均有应用背景。对于空中目标，微动特征可用于旋翼飞机低空悬停检测、固定翼飞机和直升机的鉴别；对于地面目标，微动特征可用于卡车和履带车的识别，也可以用于探测识别行人、雷达天线的转动以及在海上颠簸的舰船等；在弹道导弹攻防对抗中，由于受作战要求的限制如有限载荷、弹道设定和大气干扰等因素，使得目标的质量分布特征和运动特征尤其是相互作用和外界干扰激励的振动、翻滚和进动等小幅运动的控制能力目前还较低。因此，微动特征对于空间目标探测与识别具有重要意义，其重要价值正越来越受到国内外学术界的关注[4-11]，并取得了很多研究成果。其中，美国海军导弹防御委员会对海基防御雷达用于弹道导弹防御进行过论证[12-13]，论证结果称，对于导弹防御雷达系统来说，微动特征能使雷达能够将弹头从诱饵中识别出来。

由于微动目标雷达回波具有非线性、多分量性等特征，需要相应的具有高分辨力、低交叉项、大的动态范围（Detectable Dynamic Range，DNR）的分析工具，才能较好地揭示目标微多普勒特征。而稀疏分解方法中的匹配追踪（MP）具有时域高分辨能力，对于信号细微特征提取具有很好的效果，基于此，研究了基于匹配追踪的微多普勒频率估计问题。

本文首先分析目标的微动特性，建立了回波模型；然后，根据微动目标的微多普勒特性建立过完备原子库，对信号进行多参数的过完备原子分解；最后，采用匹配追踪方法，得到目标的微多普勒频率，仿真验证了该方法的有效性。

1 微动目标多普勒频率提取算法

1.1 微动目标回波模型

假设雷达发射窄带相参信号为

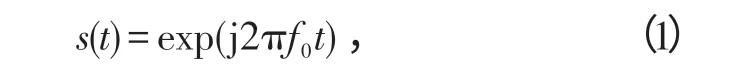
式中：f0为雷达工作频率；t为时间。

设点目标的平动速度为v，回波信号为：

式（2）中：a为与目标散射强度有关的常量；；c为光速；弹头距离雷达的初始距离为R0；散射点P距离雷达的瞬时径向距离为r(t)=R0+vt+rmicro(t)，rmicro(t)为目标微动引起的径向距离。则多普勒频率为：

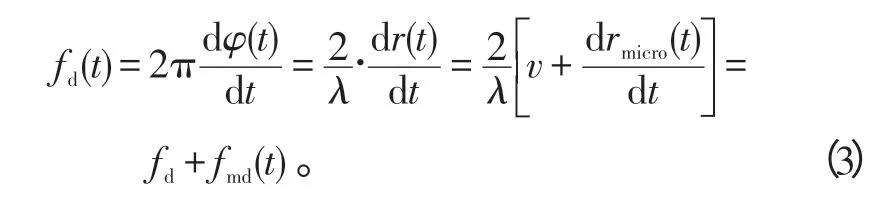
由式（3）可以看出，目标回波多普勒频率由2部分组成，fd表示平动产生的多普勒频率，fmd(t)表示微动产生的多普勒频率，即微多普勒频率。其中，fmd(t)为周期性函数，由于fd相对于fmd(t)是个缓变量，这里假设为一常量。设雷达入射波为均匀平面波，根据对微动模型的微动形式的分析，基本微运动形式引起的多普勒频率为正弦形式，因而信号微动模型可写成以下统一形式：

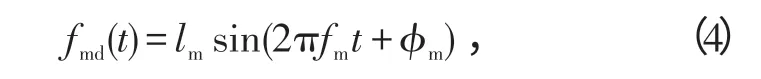
式中：lm为幅度调制因子；fm为频率调制因子；ϕm为初相因子。

其中，正弦调制项中的角频率有目标的微动角频率决定，幅度和初相位由雷达波长、目标与雷达的相对位置和目标散射点的分布决定。

由于微动目标回波中由平动引起的多普勒频率是一致的，微动目标和雷达之间相对的平动可以通过魏格纳瑞利谱峰法补偿。通过补偿即可剔除回波中的平动分量，即多普勒频率。在经过微多普勒分离与提取后，回波信号即为如下正弦调频信号：

可见，微动目标雷达回波符合多分量AM-FM 信号模型，分量信号的调频参数反映了目标微动特性，为简化讨论，在理想散射中心的假设下，忽略分量信号的调幅和初相参数，干扰信号回波模型为

式中：Ai为回波幅度；I为微动目标个数；fm,i为各微动目标频率调制因子。

1.2 过完备原子库构建

假设回波信号s(t)离散后长度为N，记为s(n)，n∈[1,2,…,N]，为了保证进行匹配追踪时信号分量的完整性和分离性，选择的分解原子必须与被分解信号相匹配，根据干扰回波信号的数学模型式（6），建立原子gn：

式（7）中，fmD-u为回波信号的微多普勒频率。

首先根据微动信号的微多普勒频率，设定搜索精度和范围。 假设搜索范围fmD-u的取值为fmD-u∈[0,U]ΔfmD-u，u=1,2,…,U，U为微多普勒频率的搜索个数，ΔfmD-u为微多普勒单元，构造的过完备原子库G为U×N的矩阵：

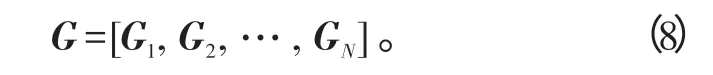
式（8）中：Gn=[gn(fmD-1)gn(fmD-2) …gn(fmD-U) ]，n=1,2,…,N，N为信号采样个数。

字典中的原子gn匹配了干扰信号包含的真实信号微多普勒和虚假信号微多普勒特征。为了保证分解系数具有足够的稀疏性以及匹配追踪的重建精度，可以通过增加原子个数U提高变换矩阵的冗余性来增强信号逼近的灵活性，进而提高信号的稀疏表示能力。信号在原子库上的投影可以表示为

由于原子库G是非正交的和冗余，多个正弦信号通过过完备字典的稀疏分解，将会在不同分量上得到最大匹配，而噪声不具有正弦信号特征，因而在这些分量上投影接近0，如图1 所示，该图为2 个目标的原子能量示意图。

1.3 基于匹配追踪的微多普勒频率估计

将过完备原子库中G的原子gn与干扰信号进行匹配程度比较，选择与信号最匹配的一组基gn(fmD-u)，使其满足

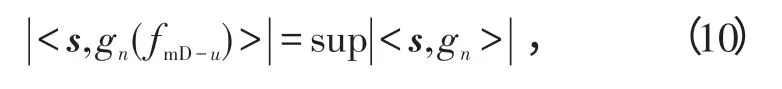
图1 两目标的原子能量示意图Fig.1 Atomic energy schematic diagram of two targets

式（10）中，＜s,gn(fmD-u)＞是干扰信号s与原子gn(fmD-u)的内积。

因此，信号可以分解为在最佳原子上的分量和残余2部分，即

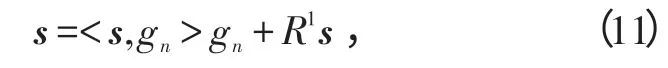
式中，R1s是用最佳原子对原信号进行最佳匹配后的残余。从原子库中将最匹配的这组基删掉，接下来对最佳匹配后的残余不断进行上面同样的分解过程，即

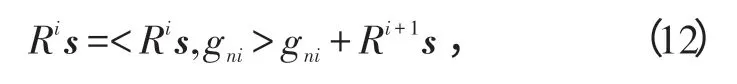
式中，i表示分解次数，根据信号分解的残差与原子库的相干性来判定分解是否完成。

假设λ2为信号s与原子库G的相干比，它取决于信号残差与原子向量之间的相关性，根据原子库的构造，确定λ2的值，假设经过L步分解后停止分解，信号被分解为

此时用少量的原子L（相对于信号长度N而言，L≪N）就可以表示信号的主要成分，即

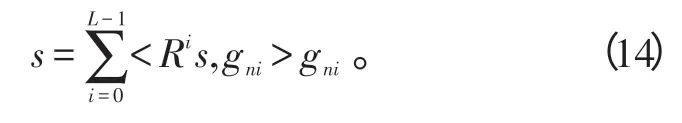
经过上述对信号s(t)的MP分解，得到信号的稀疏解能量图xˆ，如图2 所示。找到最大峰值的坐标Am(u)，u∈(0,U)；根据以下公式得到各个目标的微多普勒频率：

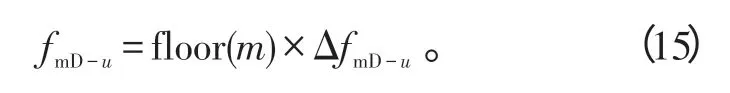
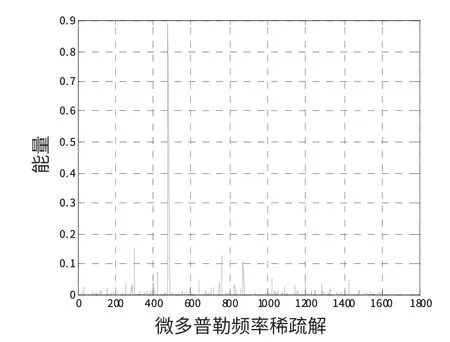
图2 稀疏解分解图Fig.2 Energy distribution of solution

2 仿真验证

为了说明该算法的有效性，本文以进动和摆动为例，研究基于MP 的2 个微动目标微多普勒频率估计问题。本文分别在不同信号持续时间和信噪比条件下进行仿真验证。图3 是进动的示意图，坐标原点O为其质心，目标绕其对称轴Oz自旋，同时绕某一矢量方向O′C旋转，由于弹头的运动是进动，因而Oz与O′C的夹角不变；图4是摆动的示意图，没有旋转等姿态控制手段，以O′点为中心在O′C与O′z所确定的平面内摆动。

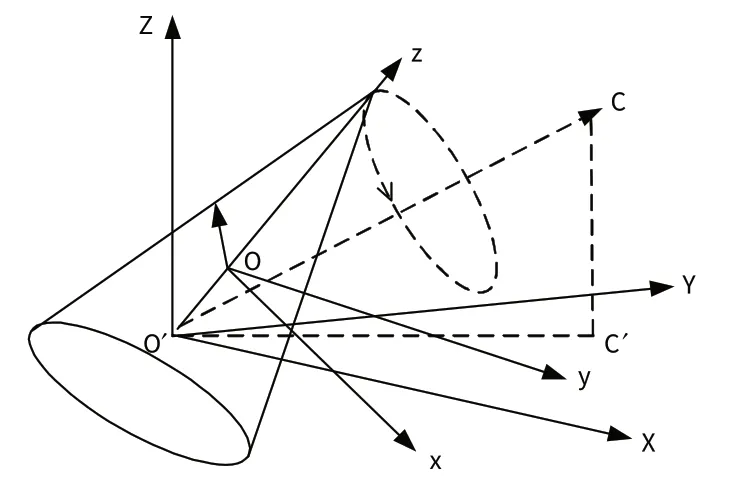
图3 进动模型Fig.3 Precession model

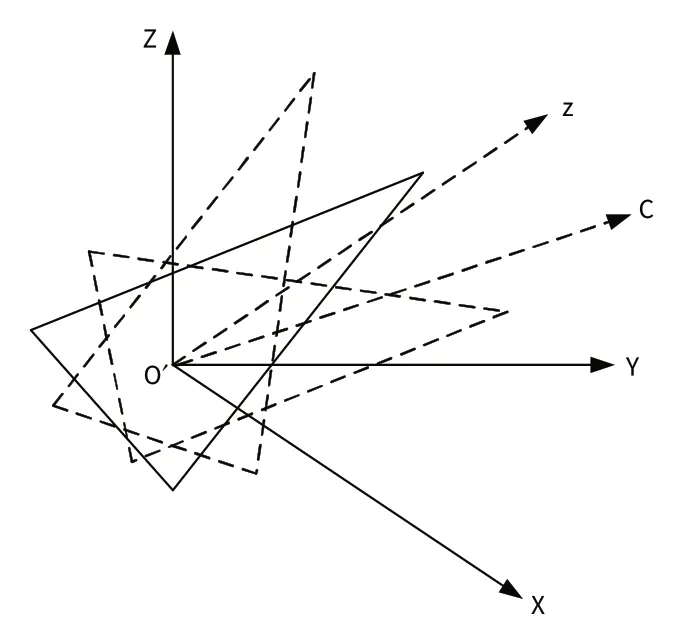
图4 摆动模型Fig.4 Wiggle model

假设雷达在t时刻发射载频f=10 GHz 的单频信号s′(t)=exp()j2πft，雷达波长λ=3 cm，雷达信号积累时间T=10 ms，采样间隔Ts=5×10-5s，MP 算法中λ2取值为0.3。假设目标进动频率为fmD-u1=6 Hz、摆动频率为fmD-u2=3 Hz，原子个数U设定为1 600。为了方便研究目标微动特性，假设真假弹头和雷达之间相对的平动已经通过相应的补偿手段补偿掉，只剩下微动特性，根据上述条件，可建立目标信号模型为：

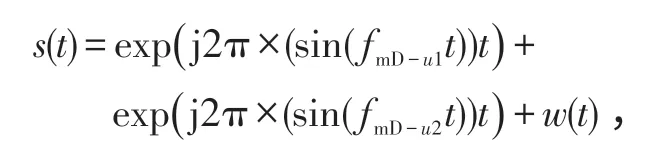
式中，w(t)为均值为0、方差为1的高斯白噪声。

2.1 不同信号持续时间条件下仿真结果

假设SNR=0 dB，表1 为不同信号持续时间T条件下真假弹头多普勒频率估计值。从仿真结果可以看出当信号时长T＞4 ms 时，本文方法能精确估计出真假弹头微多普勒频率，但随着信号时长的减小，真假弹头的微多普勒频率估计精度慢慢降低，当T=3 ms，其微多普勒频率估计结果已严重失真。图5和图6 分别为信号持续时间T=5 ms 和T=2 ms 时的稀疏解分解图。

表1 不同信号持续时间条件下真假弹头多普勒频率估计值Tab.1 Estimation of Doppler frequency for different time duration

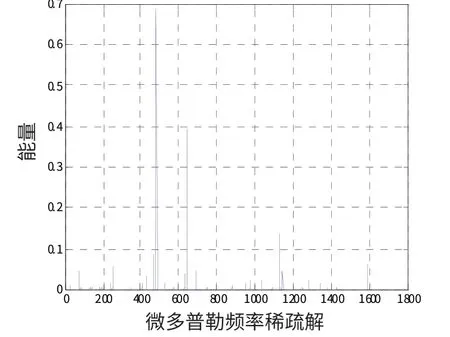
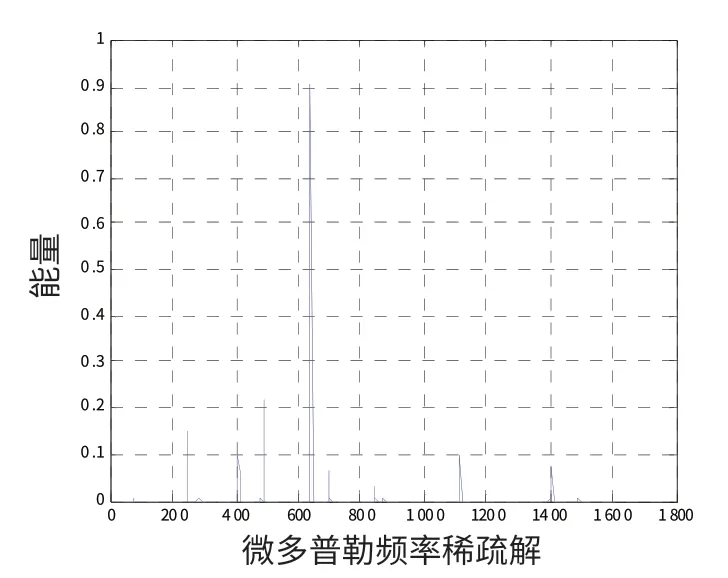
图6 T=2 ms 时的稀疏解分解图Fig.6 Energy distribution of solution when T=2 ms

2.2 不同信噪比条件下仿真结果

假设信号持续时间T=10 ms，表2 为不同信噪比条件下微多普勒频率估计值，从仿真结果可以看出在信噪比SNR ＞-4 dB 时，本文方法精确估计出真假弹头微多普勒频率，但随着信噪比的降低，微多普勒频率估计精度慢慢降低，当SNR=-8 dB，其微多普勒频率估计结果已严重失真。

图7、8 分别为信号持续时间SNR=-2 dB 和SNR=-8 dB 时的稀疏解分解图。

表2 不同信号持续时间条件下真假弹头多普勒频率估计值Tab.2 Estimation of Doppler frequency for different SNR

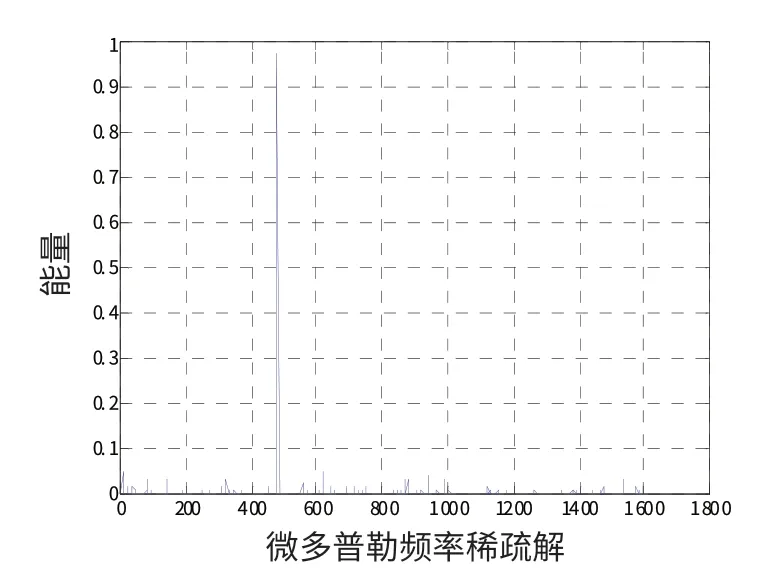
图7 SNR=-2 dB 时的稀疏解分解图Fig.7 Energy distribution of solution when SNR=-2 dB

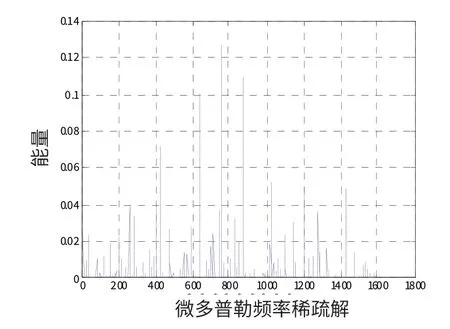
图8 SNR=-8 dB 时的稀疏解分解图Fig.8 Energy distribution of solution when SNR=-8 dB

3 结论

本文给出了一种基于正交匹配追踪的真假弹头微多普勒提取算法，分析了真假弹头微动特性，建立了真假弹头的回波模型，并在不同信号积累时长、信噪比条件下分别对本算法进行了仿真，仿真结果表明本算法具有微多普勒频率的估计精度高，且不受交叉项干扰的特点。

[1] LOVETT A，SHEN C，OTAGURO W. Microdoppler：non- cooperative target classification/dentification，A420040，AD[R]. Maryland，USA：Naval Air Warfare Center Aircraft Division，2004.

[2] CHEN V C. Analysis of radar micro-Doppler signature with time- frequency transforms[C]//IEEE Proceeding Workshop on Statistical and Array Processing.PA：PoconoManor，2000：463-466.

[3] CHEN V C，LI F，HO S，et al.Micro-doppler effect in radar phenomenon，model，and simulation study[J]. IEEE Transactions on Aerospace and Electronic Systems，2006，42（1）：2-21.

[4] SPARR T，KRANE B. Micro-doppler analysis of vibrating target in SAR[J]. IEEE Proceedings on Radar Sonar Navigation，2003，150（4）：277-283.

[5] 陈行勇.微动目标雷达特征提取技术研究[D].长沙：国防科技大学，2006.

CHEN HANGYONG. The research status of radar target feature extraction for micro-motion[D]. Changcha：National University of Defense Technology，2006.（in Chinese）

[6] THAYAPARAN T，ABROL S，RISEBOROUGH E，et al.Analysis of radar micro-Doppler signatures from experimental helicopter and human data[J]. IET Radar Sonar Navigation，2007，1（4）：289-299.

[7] 黄健，李欣，黄晓涛，等.基于微多普勒特征的坦克目标参数估计与身份识别[J]. 电子与信息学报，2010，32（5）：1050-1055.

HUANG JIAN，LI XIN，HUANG XIAOTAO，et al. Micro- Doppler features based parameter estimation and identification of tank[J]. Journal of Eleetronics & Information Technology，2010，32（5）：1050-1055.（in Chinese）

[8] 陈行勇，刘永祥，黎湘.雷达目标微多普勒特征提取[J].信号处理，2007，23（2）：222-226.

CHEN HANGYONG，LIU YONGXIANG，LI XIANG.Extraction of micro-doppler featrue of radar[J]. Signal Processing，2007，23（2）：222-226.（in Chinese）

[9] 陈行勇，刘永祥，黎湘.微多普勒分析与参数估计[J].红外与毫米波学报，2006，25（5）：360-363.

CHEN HANGYONG，LIU YONGXIANG，LI XIANG.Analysis of micro-doppler and parameters estimation[J].Journal of Infrared and Millimeter Waves，2006，25（5）：360-363.（in Chinese）

[10] ZEDIKER M S，RICE R R，HOLLISTER J H. Method for extending range and sensitivity of a fiber optic micro-Doppler ladar system and apparatus therefore：U.S.，5847817[P].1998.

[11] RENHORN I，KARLSSON C，LETALICK D. Coherent laser radar for vibrometry：Robust design and adaptive signal processing[J]. SPIE Proceedings on Applied Laser Radar Technology，1995，2472：23-30.

[12]CHEN V C，LI F，HO S，WECHSLER H.Analysis of micro-Doppler signatures[J]. IEEE Proceedings on Radar，Sonar and Navigation，2003，150（4）：271-276.

[13] CHEN V C. Micro-Doppler effect of micro-motion dynamics：a review[C]//Proceedings of SPIE on Independent Component Analyses，Wavelets，and Neural Networks.Orlando，2003：240-249.