水平轴潮流能水轮机设计与数值模拟

盛其虎，赵东亚，张亮

(哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001)

当今社会能源短缺问题已变得日益严峻，作为一种清洁可再生能源，海洋潮流能具有储量丰富、分布集中及可预测性强等特点。如何高效开发利用潮流能已受到国际社会的重视。

水轮机是一种常见的潮流能发电装置，可分为垂直轴水轮机和水平轴水轮机。水平轴水轮机和水平轴风力机原理相近，具有输出功率稳定的特点。1994年英国IT动力公司设计的风车式发电装置、2003年英国MCT公司研制的出首台商业规模的潮流发电装置均为水平轴形式的水轮机［1-2］。我国由哈尔滨工程大学设计的10 kW水平轴水轮机已于2012年成功投入运行。

叶片是潮流能水轮机能量转换设备的关键部件，直接影响能量转换的效率。叶片的性能主要取决于翼型形状以及叶展形状。前者根据翼型的气动性能选择，后者主要由沿展长方向各站面叶素的弦长和安装角决定。风力机叶片形状的设计主要有基于圆盘理论的简化设计模型，基于涡流模型的Schmitz设计模型、Glauert设计模型和Wilson设计模型。由于Wilson模型考虑了轴向、切向诱导系数，并且计入叶尖叶根损失，使得设计结果具有较高的精度［3-4］。本文选用Wilson模型进行水轮机叶片设计，并对设计的水轮机进行数值模拟以预测其水动力性能。

1 叶片设计的叶素动量理论

叶素理论的基本思想是:将叶片沿展长方向分成许多微段，这些微段称为叶素，当考虑轴向和径向速度诱导因子a、b时，叶素周围速度分布如图1所示。

图1 叶素周围流速及受力Fig.1 Flow and forces on blade element

叶素在合速度为W的流体作用下，所受流体力可以分解为垂直于W的升力L和平行于W的阻力D，ω为叶轮旋转角速度，V为来流速度，r为剖面半径，且有:

式中:Cl、Cd分别为该叶素在攻角α下的升、阻力系数，c为叶素弦长。

叶素－动量定理(blade element momentum，BEM)的基本假定是:叶素所受力仅与通过叶素扫过的圆盘的流体的动量变化有关，即叶片受力等于流过流体的动量变化率［5-6］。由此可在轴向和切向建立如下等式:

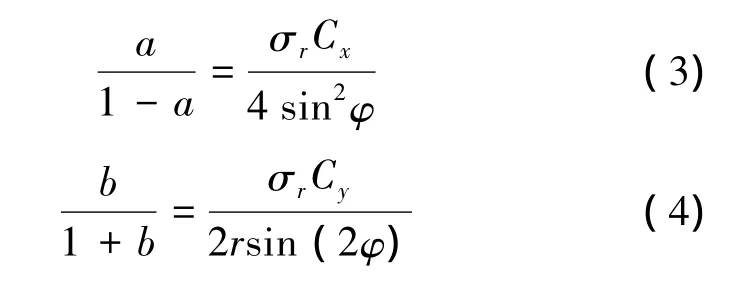
定义叶尖速比λ:

式中:R为水轮机半径。

对于不脱体的粘性绕流，阻力D是由于叶片表面的摩擦力产生的，在通过叶轮时并不影响压降，因此在确定诱导因子时排除阻力因素Cd的影响。

考虑叶尖、叶根损失影响时需对BEM方程进行修正，本文采用Prandtl近似法确定的叶尖、叶根损失因数ftip、fhub分别为［7］

将总损失系数f=ftipfhub代入动量方程可得约束条件:

沿叶片展长方向取不同的截面，以产生的功率最大为设计优化目标。在各界面处，由单位叶素做功可得目标函数:

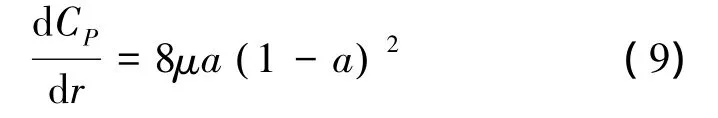
利用Matlab中的fmincon工具进行最优化计算，便可得求各站面处的诱导因子a、b。进而可求得安装角:

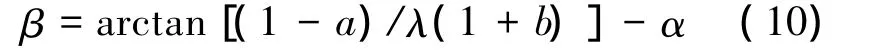
式中:α为升阻比最大时的攻角，与具体翼型有关。

将诱导因子代入式(3)或者式(4)，即得对应截面的弦长值。

2 水轮机的设计参数

中国潮流能资源分布调查显示:流速在1.28～2.04 m/s的潮流蕴含的能量高1.13 GW［8］。尽管某些水道的流速可以达到3 m/s，但总能量较低，开发价值不大。为使设计的水轮机能有较大的工作范围，本文选取V=1.6 m/s为水轮机设计工作环境流速。

定义水轮机能量利用率Cp和推力系数Ct为

水轮机的直径Z可由下式给出:

式中:Pexp=10 kW为水轮机设计功率，Cp=0.4为预测的水轮机能量利用率，η=0.95为装置的机电效率，ρ=1.025 kg/m3为海水密度。

叶片翼型采用NACA63-8XX系列，该系列翼型具有较高的升力系数。为保证叶片的结构强度，翼型的相对厚度沿展长方向递减。轮毂直径取为1/10叶轮直径。取叶尖速比λ=6时的转速为设计转速。

将叶片沿展长划分为17个站面，根据约束条件求解目标函数可得各站面的参数如表1示。

表1 叶片参数Table 1 Parameters of blade

对于单位翼型，依据求得的弦长和安装角进行坐标变换得到各剖面的优化翼型。为减小轮毂形状对流场的影响，轮毂两端采用圆弧面过渡，建立的三维模型如图2示。

图2 水轮机三维模型Fig.2 Turbine＇s 3D model

3 数值计算

3.1 求解区域网格划分与设置

本节对设计的叶轮进行CFD模拟以预测其工作性能，验证设计的合理性。水轮机的性能验证采用商业软件 CFX，利用 ICEM-CFD进行网格划分［9-10］。

本次数值模拟在长方体形状的流体域内进行，内部建立圆柱旋转域以模拟水轮机转动。其中叶轮中心距入口为4倍叶片展长，距出口12倍叶片展长，距四周边界为3倍叶片展长。对于流体域采用结构网格划分，由于叶轮表面的形状很不规则，旋转域内采用非结构网格并在叶轮表面添加边界层。生成的网格数据如表2示。

表2 网格数据Table 2 Mesh data

湍流模型采用 Shear Stress Transport模型。SST模型结合了κ-ε模型与κ-ω模型的优点，在靠近壁面部分采用κ-ω模型，在远处的自由剪切流动采用κ-ε模型。由于考虑了湍动剪切应力，SST湍流模型能很好地预测并计算逆压梯度下流动的分离。

对于计算域的边界，入口选择为速度入口;出口为压力出口，相对压力为0，参考压力为1个大气压，且不考虑重力;其余4个流体域边界设为墙壁;叶轮表面为无滑移壁面。

3.2 数值方法的验证

CFD数值模拟方法的可靠性可以采用与实验数据对比的方法进行验证。本文根据南安普顿大学公布的三叶片水轮机模型的实验数据进行模拟计算，该模型直径为0.8 m，采用NACA 63-8XX系列翼型［11］，选取流速V=1.73 m/s时的计算工况，得到的数值模拟结果如图3所示。

图3 能量利用率和推力系数对比Fig.3 Comparison of power and thrust coefficients

可以看出:模拟结果与实验值较为一致，尤其是在设计的最佳叶速比附近。最大误差出现在较高或较低叶速比时，但最大误差小于10%。由此可以认为该方法能很好地模拟水轮机的水动力性能。

4 计算结果与分析

4.1 水轮机的功率与推力特性

设定流速为1.6 m/s时，在不同叶速比时水轮机的功率和推力特性计算结果如图4所示。

图4 水轮机功率和推力特性Fig.4 Power and thrust properties of blade

由图4可知，在初始阶段，水轮机的效率随转速增大而逐渐提高，并在叶速比λ=6附近时达到最大值。说明水轮机满足了在设计叶速比下的功率要求。当转速高于设计转速时，水轮机效率开始下降。但与低转速时相比，水轮机在高转速时具有较高的效率。水轮机的推力系数随叶速比增大急剧增加。在低转速比时，推力以线性趋势上升;当转速比较高时，速率增长有所放缓。

4.2 叶展长方向单位长度输出功率分布

由于叶片在展长方向不同截面处的弦长攻角差异，叶片各处受力和输出的功率不均。图5为水轮机叶片单位长度输出功率随叶片展长的变化。r＜0.4 m的部分为轮毂及轮毂和叶片间的过渡部分，不考虑其输出功率。

图5 展长方向单位长度输出功率Fig.5 Power output along spanwise direction

单位长度输出功率沿叶片展长大致呈抛物线分布。从0.4 m＜r＜0.9 m的部分单位长度输出功率呈近乎线性的增长，并在r=1.3 m的附近达到最大值。在0.9 m＜r＜1.7 m的范围内输出功率始终保持较高的值，但在1.7 m＜r＜2 m的范围内出现急剧下降，在叶尖处降为负值，这一现象和叶尖处流场的三维效应有关。

4.3 三维流动特性分析

在叶片设计中，叶素理论截取叶片沿展长方向的剖面，将三维叶片简化为二维剖面进行分析;叶素－动量理论中假定轴向诱导因子沿展长方向不变，即流体无径向的流动。但在实际三维流场中，压力的分布不均会导致流体的径向流动。

为研究三维效应对水轮机特性的影响，提取三维流场中半径为0.4、1.3、1.9、1.99 m的叶片截面压力值，同时对这些截面处的翼型进行对应攻角和流速下的二维模拟计算。

定义压力系数Cpre:

各截面的压力系数分布如图6示。可以看出在r=0.4 m处三维流场的压力系数分布与二维数值模拟的结果差别较大。三维流场中该处压力面与吸力面的压力绝对值很低，上下表面的压差很小，并将导致产生的力矩较低。这是因为靠近轮毂处流场流动复杂，三维效应强烈，叶片上下表面的压差会诱导出侧向的绕流，从而平衡上下表面的压力值。

在r=1.3 m截面处的压力系数值和二维计算结果吻合很好。这说明叶片中部的绕流有很强的二维性。但导边处的压力值波动较大，这是因为由于该处存在着很大的压力梯度，而且靠近前驻点的位置流速较低，使得流动易受到临近截面的干扰而产生沿径向的流动。

r=1.9 m处三维绕流的压力分布和二维模拟结果开始出现差值。具体表现为压力面的压力下降，吸力面的压力上升，导致压差减小。到r=1.99 m处，压力分布与r=0.4 m处的已十分相似。绕叶尖端部的绕流(图7)使得叶片上下面的压差被抵消，甚至在压力面出现了负压。

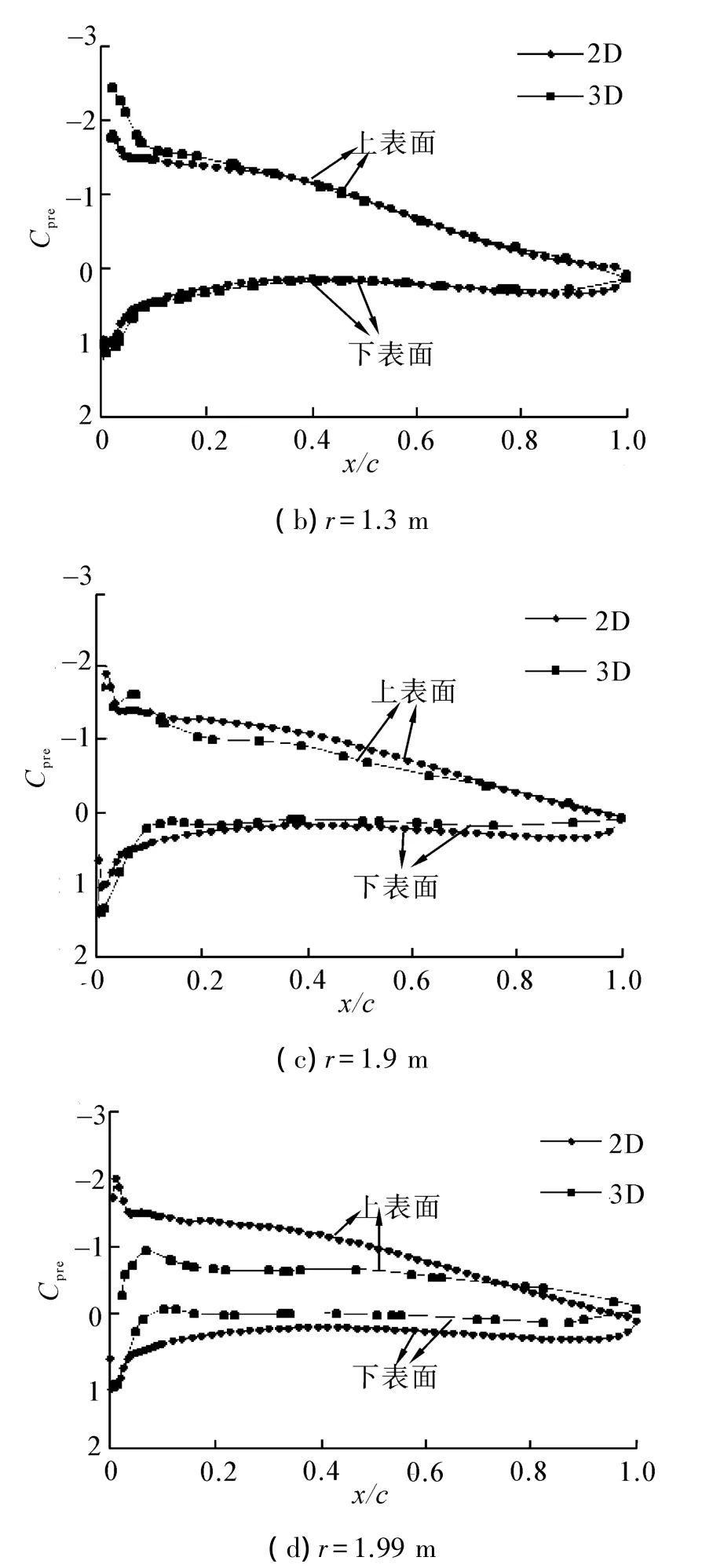
图6 二维与三维模拟的压力系数比较Fig.6 Pressure coefficient comparison between 2D and 3D simulation

图7 叶尖绕流流线分布Fig.7 Streamline distribution on blade tip

4.4 叶片表面流场分析

鉴于流场沿叶片展长的变化，对叶片表面流场的流线分析可以给出更为直观的流动情况。

图8为叶片表面的流线图，可以看出:叶展中部的流线较为均匀，且与叶片截面平行。叶根和叶尖部位的流线有偏移，说明该处流场有径向方向的流动。同时叶片导边处流场亦有明显的径向流动。

图8 叶片吸力面流线分布Fig.8 Streamline distribution on suction surface

从图8还可以看出:流线未在叶片表面终止或产生环形绕流，这说明尽管叶片吸力面有明显的逆压梯度，但翼型尾部表面流动并未将至0，附面层的厚度没有积累起来，未发生边界层分离。因此不会导致叶片的失速。从r为0.4、1.3、1.9 m处的截面流线分布(图9)也可观察到，叶片周围绕流比较有规律。即便是在具有大攻角的叶根(r=0.4 m)处，除了少许沿展长方向的流动引起的在叶片表面的流线终结，叶片表面的流动表现出很好的层流性质。

图9 叶片截面流线分布Fig.9 Streamline distribution around blade profile

5 结论

本文基于叶素－动量理论进行了潮流能水轮机的设计，并用CFX进行数值模拟证明了水轮机的工作性能达到了设计要求。由研究结果可知:

1)叶片设计的叶素－动量理论忽略展长方向的流动，为准确预报水轮机功率特性，在确定叶片弦长、安装角时，必须考虑三维损失系数。

2)输出功率主要由叶片中间部分产生。该段叶片受三维效应影响较小。而且由于各截面弦长差别不大，产生功率的大小受截面处线速度影响明显，靠近外侧部分输出功率较大。

3)水轮机的三维数值模拟结果和对应工况下的二维数值模拟结果存在一定的误差，尤其是在叶根、叶尖处误差很大。因此只有叶片中部的流线与截面相对平行，可采用二维分析;叶尖与叶根处截面的二维分析则失真严重。

4)叶片较小的弦长和较大的线速度成功避免了边界层分离现象的发生。使得输出功率稳定，不易产生振动。

本文的分析主要针对水轮机水动力性能和周围流场的分析，并未考虑载荷对叶片结构的影响和叶片变形对流场的反作用［12］，同时水轮机在真实的工作环境下还有可能发生空化现象。这些问题都有待进一步的研究。

［1］FRAENKEL P L.Power from marine currents［J］.Journal of Power Energy，2002，216:1-14.

［2］李志川.垂直轴潮流能水轮机水动力特性数值模拟和实验研究［D］.哈尔滨:哈尔滨工程大学，2011:4-12.

LI Zhichuan.Numerical simulation and experimental study on hydrodynamic performances of vertical axis tidal turbine［D］.Harbin:Harbin Engineering University，2011:4-12.

［3］JO C-H，KIM D Y，RHO Y H，et al.FSI analysis of deformation along offshore pile structure for tidal current power［J］.Renewable Energy，2013，54:248-252.

［4］韩璐.水平轴风力机叶片设计及气动性能研究［D］.南京:南京航空航天大学，2008:28-32.

LU Han.Design and experimental research on aerodynamic performances of horizontal axial wind turbine blade［D］.Nanjing:Nanjing University of Aeronautics and Astronautics，2008:28-32.

［5］GAO Qiuxin，JIN Wei，VASSALOS D.The calculations of propeller induced velocity by RANS and momentum theory［J］.Journal of Marine Science and Application，2012，11 (2):164-168.

［6］YAVUZ T，KOC E.Performance analysis of double blade airfoil for hydrokinetic turbine applications［J］.Energy Conversion and Management，2012，63:95-100.

［7］BURTON T，SHARPE D，JENKINS N，et al.风能原理［M］.武鑫，译.北京:科学出版社，2007:72-75.

［8］WANG Chuankun，LU Wei.Analysis method of ocean energy resource and storage estimation［M］.Beijing:Ocean Publisher，2009:6-9.

［9］HE Miao，WANG Chao，CHANG Xin，et al.Analysis of a propeller wake flow field using viscous fluid mechanics［J］.Journal of Marine Science and Application，2012，11(3): 295-300.

［10］WANG Qiang，ZHOU Hu，WAN Decheng.Numerical simulation of wind turbine blade-tower interaction［J］.Journal of Marine Science and Application，2012，11(3):321-327.

［11］BAHAJ A S，MOLLAND A F，CHAPLIN J R，et al.Power and thrust measurements of marine current turbines under various hydrodynamic flow conditions in a cavitation tunnel and a towing tank［J］.Renewable Energy，2007，32(3):407-426.

［12］BAZILEVS Y，HSU M C，SCOTT M A.Isogeometric fluidstructure interaction analysis with emphasis on non-matching discretizations，and with application to wind turbines［J］.Computer Methods in Application and Mechanics Engineering，2012(1):28-41.