有毒易燃气体扩散中人员救援疏散数学模型

李秀林，段耀勇，庞 坤

（中国人民武装警察部队学院 基础部数学教研室，河北 廊坊 065000）

有毒易燃气体扩散中人员救援疏散数学模型

李秀林，段耀勇，庞 坤

（中国人民武装警察部队学院 基础部数学教研室，河北 廊坊 065000）

应用数学方法，基于高斯扩散模型和梯度概念，给出了地面连续泄露源和瞬时泄露源的人员救援疏散模型，得到了疏散最优路线，可解决易燃易爆或有毒气体泄露扩散中人员疏散路线问题，预测的路线可为现场处置人员提供参考依据，对预防和减小灾害后果的严重程度具有重要意义.

高斯扩散模型；梯度；疏散路线

在毒性气体物质如乙炔、天燃气等的运输和储藏中，常因装置失效等各种原因泄漏，有毒气体飘散形成大面积的毒害区，会导致人员伤亡事故的发生.因此，研究气体泄漏过程中人员救援疏散的数学模型，确立疏散的最优路线，对于预防减小灾害后果的严重程度具有重要意义.

1 气体泄漏扩散数学模型

气体泄漏气体相对密度小于和接近1，泄漏后会形成气团，其扩散模型多采用高斯模型.以储罐的泄漏点为坐标原点，平均风向与与x轴平行，并与x轴正向同向，空间一点(x, y,z)处的质量浓度计算公式为[1]：

连续泄漏时：

瞬时泄漏时：

其中：ρ(x,y,z)为空间一点(x,y,z)处的浓度（kg/m3）；μ：平均风速（m/s）；x0,y0,z0为烟团中心坐标；δx,δy,δz为x,y,z方向上的扩散参数（m）.我国GB3840－91《制定地方大气污染物排放标准的技术方法》采用如下经验公式确定扩散参数，r1、σ1、r2及σ2称为扩散系数[2].这些系数由实验确定，在一个相当长的x距离内为常数，可从GB3840－91的表中查取.

2 扩散救援疏散的数学模型

基于某一场函数ρ其梯度是函数值上升或下降变化率最大的方向，我们应用这一概念来建立气体泄漏扩散救援疏散的数学模型.

2.1 连续泄漏扩散救援疏散的数学模型

气体连续泄漏强度在泄漏一段较长时间内可视为稳定，取作常数，扩散的流场可认为是稳定场，即扩散空间某一点的浓度是恒定的，不随时间改变.即假设气体泄漏周围地表为平原，空间中的一点M(x,y,z)处的梯度也即gradρ，是此点浓度函数上升或下降变化率最大的方向：

扩散问题中最关心的是地面浓度的分布情况，令z=0，所处位置在正下方向，y0=0,z0=h.则（1）式变为

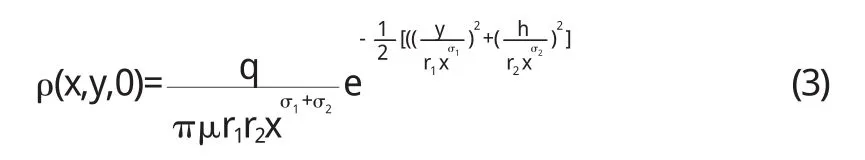
假设当时被救援人员处在M0(x0,y0)位置，经检验，gradρ的的反方向是浓度函数下降变化率最大的方向.假定人员的运动速度恒为v0，则最优路线的数学方程表达式为

因此，气体连续泄漏情况下，人员疏散的最优路线应沿其所处位置的梯度的反方向（浓度下降变化率最大）逃生，即可在短时间内达到安全的地方.

2.2 瞬时泄漏扩散救援疏散的数学模型

对于气体瞬时泄漏的情况，在下风方向时刻t的气团中心坐标为：x0=u·t,y0=0,z0=h，在（2）中令 ，则

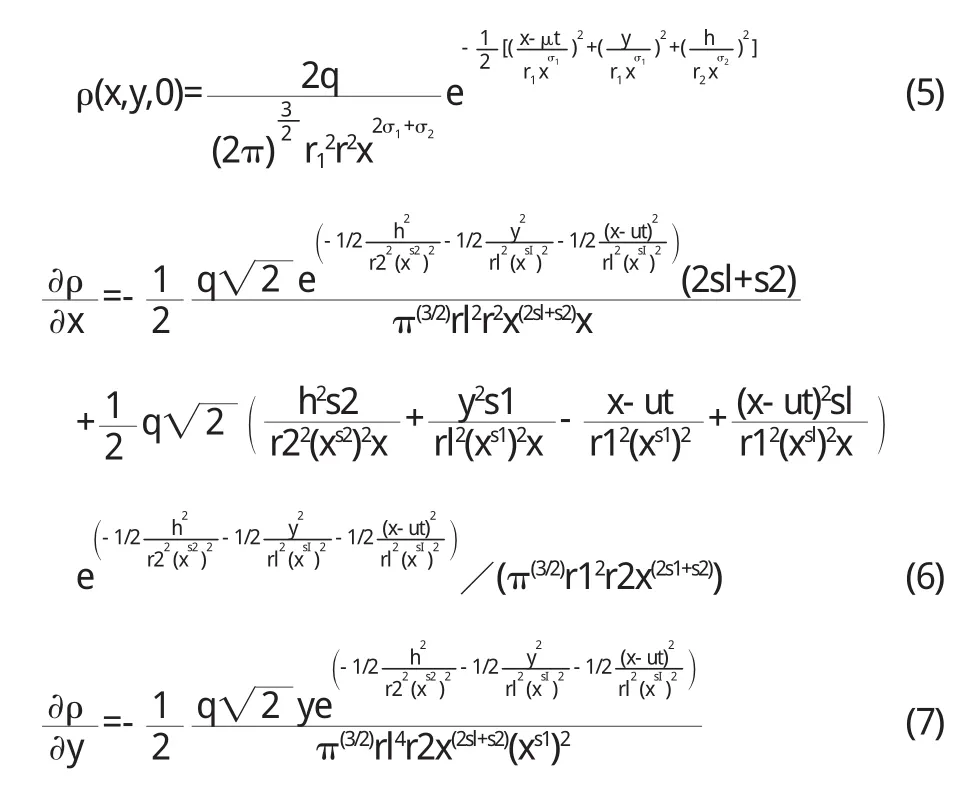
其中，上式中用s1,s2分别代替ρ(x,y,z)的σ1和σ2.

由（5）可知空间一点浓度与时间有关，系非稳定场.为此，我们把时间离散，在较小的一段时间Δt内，扩散区域的浓度场可以看作是稳定场.假设当时被救援人员处在M0(x0, y0)位置，则gradρ(x0,y0,t0)的方向决定在t0时刻人员疏散的运动方向，假定人员的运动速度恒为v0，则Δt秒后到达M1(x1, y1)处，同理gradρ(x1,y1,t1)的方向决定在t1=t0+Δt时刻人员疏散的运动方向…，其中Mi+1的坐标可以由Mi的坐标得到.假设Mi(xi,yi,ti)，那么Mi+1(xi+1,yi+1,ti+1)的坐标可用如下的数学公式得到：

连接各Mi(xi,yi,ti)，从而模拟出最优路线图.

3 应用举例

某化肥厂一辆液氨运输车，运载790kg液氨途径某乡镇集市附近，因运输车质量问题，罐后封头突然破裂飞出.液氨瞬间全部汽化，当时风速2m/s，集市位置x0=150m,y0=50.若人员疏散速度为4m/s，试给出人员疏散的最优路线.

其中相关参数如下：

经计算，在60秒时人员开始疏散时的气体浓度分布如图1（其中x，y和p单位分别为m和kg/m3）：

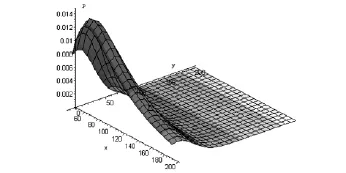
图1 60秒时的浓度分布

以下内容涉及的坐标和气体浓度单位均为m,m和kg/m3，时间单位为s.疏散节点坐标及相应浓度如表1：

表1 60-101秒间节点上的坐标和气体浓度

t x y p 81 162.6863 137.0296 2.31E-08 82 163.0432 141.0136 1.08E-08 83 163.0281 144.999 4.92E-09 84 164.3542 148.9857 2.18E-09 85 164.6651 152.9736 9.46E-10 86 163.9608 156.9626 4.01E-10 87 164.2417 160.9527 1.66E-10 88 164.508 164.9439 6.69E-11 89 164.7599 168.9359 2.64E-11 90 164.9975 172.9289 1.02E-11 91 165.2211 176.9226 3.82E-12 92 165.4308 180.9171 1.40E-12 93 165.6269 184.9123 5.03E-13 94 165.8093 188.9081 1.76E-13 95 165.9784 192.9046 6.02E-14 96 166.1341 196.9015 2.01E-14 97 166.2767 200.899 6.56E-15 98 166.4061 204.8969 2.09E-15 99 166.5226 208.8952 6.50E-16 100 101 166.6263 166.7171 212.8938 216.8928 1.97E-16 5.85E-17

60~101 秒的疏散模拟路线如图2：

图2 60~101秒的疏散模拟路线

图2为疏散坐标连线图，显然165秒后基本上沿y轴方向疏散，150~165秒之间路线的拟合函数为：

疏散路径上各节点浓度值如图3：

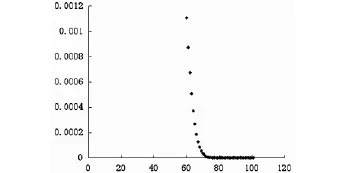
图3 60~101秒收散路径上各节点浓度值

由图3可知，疏散路线节点上的浓度值随时间的增加而急剧减小，符合我们设想的逃生原则.

4 结论

基于高斯扩散模型，应用数学方法，给出了地面连续泄露源和瞬时泄露源的疏散模型，得到了疏散最优路线，以解决易燃易爆或有毒气体泄露扩散中预测人员疏散问题，其预测的结果可为现场处置人员提供参考依据.

然而，气体泄露扩散过程与风向、风速、地形等因素有关，是一个非常复杂的问题[3]，很难用单一模型来准确刻画其泄露扩散的特征，本模型假设地形为平面，风速不变，人员疏散速度恒定，在考虑这些因素的影响下，本模型还可以进一步改进.

〔1〕彭世尼,周廷鹤.燃气泄漏与扩散模型的探讨[J].煤气与热力,2008,28(11):9-12.

〔2〕张宪法.甲醇储罐泄漏扩散及事故状态的数值模拟[J].石油化工安全环技术,2011(4):14-19.

〔3〕Pang Kun,Duan Yao-yong,LI Xiu-lin.The Study on the Improvement for Mathematical Model and the Affected Actors of Gas Storage Vessel Leakage. ICAEMT2013，Advanced Materials Research Vols.753-755 (2013)pp 2742-2746，Trans Tech Publications, Sw itzerland.

TU996.9

A

1673-260X（2014）01-0014-03

河北省科技厅计划项目资助（12275402）