等物质的量规则进展
赵建宏 赵梦月
(郑州大学化工能源学院,郑州 450002)
1 历史回顾与现状
20多年前,有关等物质的量规则的论文在化学通报等杂志上[1-3]发表后,引起原国家技术监督局单位制办公室及其所属的全国量和单位标准化技术委员会第五分委会(物理化学及分子物理学分委员会)的重视,他们认为在化学界宣传SI、贯彻国家法定计量单位的关键,是让大家理解SI的第七个基本量“物质的量”及其单位“摩尔”。“等物质的量规则”正是根据“物质的量”及其单位“摩尔”的定义提出来的,代替“当量定律”进行分析化学的计算问题。因此SI办公室在会议纪要中,建议采用等物质的量规则,促进了等物质的量规则在我国普及和发展。最近在互联网查询结果表明,有60余篇论文,50多部著作及几十所高校应用了等物质的量规则。
这些论文对等物质的量规则给予肯定的评价,认为“它完全能够取代当量定律,甚至比当量定律更优越,因它避开了当量值的可变性,也避免了求当量值的复杂性和混乱的运算规则,使化学计算全面统一在SI之中了”[4],“等物质的量规则,由物质的量定义导出,并也能由反应进度证明,具有严密的科学性,它使全部滴定分析计算规范化,简单化,并可全部利用以前的有关数据、资料,分析人员易于掌握”[5]。
许多化学家出版专著、教科书,介绍或使用等物质的量规则。武汉大学主编的“分析化学”[6],北京大学的“定量分析化学简明教程”[7]及“分析化学教程”[8],吉林大学的“化学分析”[9],复旦大学的“分析化学原理”[10],浙江大学的“分析化学习题”[11]及十几部其它高校教材都应用了这个规则。应用这个规则的专著涉及到化工[12]、冶金[13]、建材(硅酸盐工业)[14]、纺织印染[15]、医药[16]和环境监测[17]等行业。除此之外,培训教材[18],以及各种化学、化工手册[19-20],也都应用了等物质的量规则。最令人鼓舞的是等物质的量规则已被广泛地应用到国家标准中,其中最重要的两项化学分析国家基础标准是GB/T 601—2002,化学试剂﹣标准滴定溶液的准备;GB/T 602—2002,化学试剂﹣杂质测定用标准滴定溶液的制备。
由于等物质的量规则在国家标准、实际生产中及高校教学中的广泛采用,促使我们应进一步发展和完善它。同时,我们也清醒的知道还有人[21]对这个规则还很不理解,称“等物质的量规则不存在,早已被许多分析化学教材所摒弃”。这提醒大家,还有人对SI、法定计量单位和国家标准不理解,需要我们继续努力。
2 等物质的量规则基础表达式及与计量数比法的关系
当量废除后,我国化学工作者采用了两种方法,对滴定分析进行计算。一个是等物质的量规则,另一个是化学计量数比法(简称计量数比法)。两种方法都可根据化学反应计量方程进行计算。只不过计量数比法的主张者[22]仅用反应物的分子、离子作为基本单元,反对用分子或离子的特定组合作为基本单元,认为这种特定组合“不是独立存在的实体”,使同一物质具有不同的摩尔质量及浓度,例如,高锰酸钾其摩尔质量可能是M(KMnO4)或M(1/5KMnO4),浓度可能为c(KMnO4)或c(1/5KMnO4),因而不能接受等物质的量规则。
其实,这些指责都是对物质的量及其单位“摩尔”的误解。他们没有真正理解SI第七个基本物理量“物质的量”及其单位“摩尔”的含义。没有真正理解在使用物质的量及其单位“摩尔”时,必须指明基本单元。基本单元可以是原子、分子、离子和电子等粒子,或这些粒子的的特定组合。IUPAC的量和符号委员会前主席McGlashan[23]指出“特定组合不限于那些已知的或想象为独立存在的单元,也不限于由整数个原子的组合”,IUPAC绿皮书[24]也指出,基本单元可以是“人造的”,不要求是“独立存在的实体”,例如,1/2H2SO4,1/5KMnO4。同一种物质,根据需要可以选择不同的特定组合为基本单元,当然这些不同基本单元的“物质的量”、“摩尔质量”及“物质的量浓度”都不相同,但它们之间有严格的换算关系。例如,某物质B,可以选B或νBB作为基本单元,那么它们的物质的量n(B)和n(νBB)、物质的量浓度c(B)和c(νBB)及摩尔质量M(B)和M(νBB),有如下关系:
n(νBB)=(1/νB)n(B);c(νBB)=(1/νB)c(B);M(νBB)=νBM(B)
(1)
实际上,我们早就指出过[4],计量数比法很容易从等物质的量规则推导出来。对任何滴定剂T与被测物质B的反应,可用下式表示:
νBB+νTT=νCC+νDD
(2)
将反应体系中每个分子(离子)与其计量数组成的特定组合作为基本单元,可得等物质的量规则基础表达式:
Δn(νBB)=Δn(νTT)=Δn(νCC)=Δn(νDD)
(3)
或
Δn(νBB)=Δn(νTT)
(4)
已知Δn(νBB)=(1/νB)Δn(B),Δn(νTT)=(1/νT)Δn(T)
则
Δn(B)=(νB/νT)Δn(T)
(5)
式(5)就是计量数比法的表示式。不少论文对计量数比法给以负面的评价,“实际上计量数比法是过去的‘摩尔比法’,忽略了基本单元决定物质的量,仅用单一的分子,离子作为基本单元,不利于学生理解物质的量与基本单元的关系”[25],“计量数比法在较复杂的反应,在表达摩尔电导率、水的硬度、碱度、盐度时会遇到麻烦”[4]。
3 等物质的量规则的实用表达式
在分析化学计算中如何选取的基本单元,广大化学工作者对此发表了各种意见,提出了最小公倍数法[26]、单位电荷法[27]、计量数归一法[28]和最简粒子数相等法[29]等。我们在早期的几篇论文[2-3]中也提出:将得失一个电子或得失一个质子的特定组合做为氧化还原滴定或酸碱滴定的基本单元。本文从物质的反应本质上进一步论证这些方法,导出了滴定反应中基本单元及等物质的量规则实用通式。
3.1 氧化还原反应基本单元的选择
对氧化剂T及还原剂B的反应,可表示为:
T+zTe→C或1/zTT+e→1/zTC
(6)
B-zBe→D或1/zBB-e→1/zBD
(7)
其中,zT、zB分别表示一个氧化剂或一个还原剂的分子(离子)(T,B)得失电子的个数。据等物质的量规则可得:
Δn(1/zTT)=Δn(1/zBB)=Δn(e)
(8)
在氧化还原反应中,我们选择1/zTT为氧化剂的基本单元,例如,1/5KMnO4;1/zBB为还原剂的基本单元,例如,1/2H2C2O4。式(8)就是氧化还原反应的等物质的量规则表示式。它不仅表示氧化剂的基本单元1/zTT的物质的量与还原剂的基本单元1/zBB的物质的量变化量相等,而且等于反应中氧化剂或还原剂得或失电子的物质的量(Δn(e))。
3.2 酸碱反应中基本单元的选择
对酸碱反应,其半反应可用下式表示:
T-zTH+→C或1/zTT-H+→1/zTC
(9)
B+zBH+→D或1/zBB+H+→1/zBD
(10)
或
1/zBB+1/zTT=1/zTC+1/zBD
(11)
上式中,T,B分别代表一个酸、碱的分子(离子),zT、zB分别代表酸、碱分子(离子)失去或得到质子的个数。据等物质的量规则可得:
Δn(1/zTT)=Δn(1/zBB)=Δn(H+)
(12)
在酸碱反应中,我们选择1/zTT为酸的基本单元,例如,1/2H2SO4;1/zBB为碱的基本单元,例如,1/2Ca(OH)2。式(12)就是酸碱反应的等物质的量规则表示式,它不仅表示在酸碱反应中,酸的基本单元1/zTT与碱的基本单元1/zBB的物质的量的变化量相等,且等于得或失H+的物质的量(Δn(H+))。
3.3 沉淀反应中基本单元的选择
对任何沉淀反应,我们选用1/zTT,1/zBB作为阴阳离子的基本单元,式中T、B分别表示参加反应的阳、阴离子,zT、zB表示离子所带电荷数。沉淀反应的产物都是电中性,或其正负电荷数相等,则
Δn(1/zTT)=Δn(1/zBB)=Δn(e)
(13)
式(13)就是沉淀反应的等物质的量规则表示式,它表示在沉淀反应中,阴阳离子的基本单元(1/zTT,1/zBB)的物质的量的变化量相等,也表示沉淀中正负电荷数量相等。显然,上述基本单元都带有单位电荷,因此,IUPAC金皮书[30]称其为单位电荷离子,例如,1/3Fe3+,1/3PO43-。单位电荷离子,除了用于沉淀反应计算外,还广泛用于电解定律(mB=M(1/zBB)Q/F)﹑水分析中碱度(OH-+HCO3-+1/2CO32-)、硬度(1/2(Ca2++Mg2+))及离子交换树脂容量的表达。
3.4 等物质的规则实用通式
由上述可知,对氧化还原反应、酸碱反应、沉淀反应其等物质的量规则表示式可统一为:
Δn(1/zTT)=Δn(1/zBB)
(14)
上式能用于氧化还原滴定,酸碱滴定,沉淀滴定及络合滴定(zT=zB=1),因此称它为等物质的量规则实用式。基本单元1/zTT与1/zBB是和一个化学上的最简单的粒子(电子、质子、或元电荷)相应的特定组合,所以称这种确定基本单元的方法为“单位最简粒子法”。这种基本单元和反应物的结构、性质紧密相关,使得等物质的量规则,不仅能表示化学反应中的计量关系,而且也反映了反应性质。
3.5 等物质的量规则与当量定律的关系
不难看出,当量定律所涉及的克当量数,当量浓度,克当量都可用上述基本单元(1/zB)B及(1/zT)T的物质的量,量浓度及摩尔质量所代替。因而IUPAC的金皮书[30]称(1/zB)B及(1/zT)T这些和一个电子、质子、电荷相应的基本单元为当量单元。显而易见,有了物质的量及其单位摩尔之后,有关当量的各个量及当量定律都没有存在的必要,等物质的量规则实用表达式能代替当量定律。式(14)能够变为下列形式:
c(1/zTT)·V(1/zTT)=c(1/zBB)·V(1/zBB)
(15)
上式也能完全代替当量定律表示式,N(T)·V(T)=N(B)·V(B)。等物质的量规则使得应用当量定律的文献资料完全能够继承,使得化学分析标准的改写也非常简单,只要将当量浓度换成相应的物质的量浓度即可。我国新颁布的的有关化学分析的标准就是以下列浓度:c((1/6)Cr2O72-)、c((1/5)MnO4-)、c((1/2)I2)、c(Na2S2O3)、c((1/2)H2SO4)、c((1/2)CO32-)、c((1/2)H2C2O4)等代替原当量浓度而得到的。
4 等物质的量规则的应用
4.1 化合物的等物质的量规则
等物质的量规则不仅可以用于化学反应,还可以表示一定量的某元素形成的一系列化合物之间的等物质的量关系。
例如,一定量Fe生成的不同的化合物:FeO,Fe2O3,Fe3O4,Fe2(SO4)3。我们选取含有一个Fe原子的特定组合为基本单元,即FeO,1/2Fe2O3,1/2Fe3O4,1/2Fe2(SO4)3。那么,根据物质的量定义,可知这些基本单元的物质的量相等:
n(FeO)=n(1/2Fe2O3)=n(1/2Fe3O4)
=n[1/2Fe2(SO4)3]
(16)
因此,对于一定量的某元素形成的不同的化合物,只要选取含有相同个数该元素原子的特定组合为基本单元,那么这些基本单元的物质的量相等,这可称为化合物的等物质的量规则。
4.2 换算因数的导出与应用
一般分析化学教材[14]中换算因数的定义为:待测组分的摩尔质量与称量形式摩尔质量之比。这个定义是不严格的,当二者的化学式中目标元素个数不同时,它是不正确的,如FeO与Fe2O3。应用等物质的量规则,很容易导出一个简单的“换算因数”计算式。例如,重量法测矿物中FeO含量时,称量形式为Fe2O3,求算其换算因数。FeO和1/2Fe2O3两个基本单元,存在着等物质的量关系:
n(FeO)=n(1/2Fe2O3)
(17)
据摩尔质量,质量及物质的量的关系可得下式:
m(FeO)/M(FeO)=m(Fe2O3)/M(1/2Fe2O3)
(18)
m(FeO)=m(Fe2O3)M(FeO)/M(1/2Fe2O3)
(19)
上式中M(FeO)/M(1/2Fe2O3)就是FeO与Fe2O3的换算因数,只要使两物质之间建立等物质的量关系,它们的基本单元的摩尔质量的比值,即为其换算因数。在各种分析结果的表达上,可用它使某元素几种化合物的质量分数互换:
w(Fe3O4)=w(Fe2O3)M(1/3Fe3O4)/
M(1/2Fe2O3)
(20)
4.3 滴定度的求算通式
已知
Δn(1/zBB)=m(B)/M(1/zBB)
(21)
Δn(1/zTT)=c(1/zTT)·V(T)
(22)
将上二式代入等物质的量规则实用式(14),即得滴定度计算式
T(B/T)=m(B)/V(T)=c(1/zTT)·M(1/zBB)
(23)
滴定度等于滴定剂的浓度c(1/zTT)与被测物质的基本单元1/zBB的摩尔质量之积。这个计算式比较简单,不含有计量数比。
4.4 等物质的量规则在复杂滴定分析中的应用
等物质的量规则能够用于任何化学反应的计算,尤其对含有多个氧化剂还原剂及歧化反应的复杂滴定体系,其计算能像简单体系一样思路清晰、步骤简单。但利用计量数比法进行计算往往很困难。
例1同一元素形成一系列化合物的体系:Pb3O4含量的测定。含Pb3O4的样品重ms,溶于HCl溶液中,再加入K2Cr2O7溶液,使Pb2+完全沉淀为PbCrO4,过滤沉淀,将沉淀溶于HCl溶液中,加入KI溶液,然后用浓度为c(Na2S2O3)的标准Na2S2O3溶液滴定生成的I2,消耗的体积为V(Na2S2O3),求Pb3O4的质量分数。
解:据化合物等物质的量规则及等物质量规则可表示氧化剂还原剂得失电子相等,体系中各物质的等物质的量关系为:
=Δn(1/9Pb3O4)
(24)
则
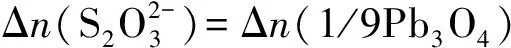
M(1/9/Pb3O4)/ms
(25)
计量数比值法提倡者的两篇文章[22,31]中都把上述的例题作为推荐计量数比法的例子。但是他们提供的解法中都首先要写出5个配平的化学反应式,然后再一步一步的找出各个物质的计量关系,显然要比等物质的量规则的解法麻烦得多。
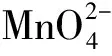
解:据等物质的量规则知,在反应中氧化剂得电子的物质的量与还原剂失电子的物质的量相等,即
(26)
则
·M(1/2HCOOH)/ms
(27)
用计量数比值法,需要写出五个反应方程式,因其中包含有岐化反应,找出有关物质的计量关系非常困难。从以上的例题,我们可以看到,对于任何复杂的测定体系,等物质的量规则都能简单、规范地计算滴定结果,然而用计量数比法,不仅要写出全部反应式,对每一步反应都要计算计量数比值,当然就很困难。
5 结语
由上述可知,等物质的量规则的实用表达式及化合物等物质的量规则不仅能科学的表达反应中各物质的计量关系,且能表示反应的实质。利用它们可导出滴定度、转换因数的简单的表达式,可继承当量定律的遗产,且使得复杂滴定体系的计算像简单体系一样简单规范。计量数比法不具备这些优点。
[1]赵梦月.当量的废除与等物质的量反应规则.化学通报,1986(5)
[2]赵梦月,吕灵翠.等物质的量规则的应用.化学通报,1992(3)
[3]Zhao Mengyue,Lu Lingcui,Abolition of the Equivalent. Rule of Equal Amount of Substance, Analytica Chimica Acta,1994(289)
[4]耿承延,白淑琴,刘啸天.等物质的量规则与反应比率法在分析化学计算中的应用.计量技术,1996(12)
[5]王玲.滴定分析结果的计算.河北农业大学学报,1998(1)
[6]武汉大学主编.分析化学第五版.北京:高等教育出版社,2010
[7]彭崇慧,李克安.修订.定量分析简明教程(第三版).北京:北京大学出版社,2009
[8]李克安.分析化学教程.北京:北京大学出版社,2005
[9]邹明珠,齐菊锐.分析化学(第二版).吉林:吉林大学出版社,2001
[10]吴性良,张继烈.分析化学原理(第三版).北京:化学化工出版社,2010
[11]浙江大学.分析化学习题集.北京:高等教育出版社,1990
[12]姜洪文.化工分析.北京:化学工业出版社,2008
[13]宋卫良.冶金化学分析.北京:化学工业出版社,2008
[14]徐伏秋,杨刚宾.硅酸盐分析.北京:化学工业出版社,2009
[15]曾林泉.印染分析化验手册.北京:中国纺织工业出版社,2007
[16]倪坤议.药物分析化学.吉林:长春出版社,2000
[17]李青山.水环境监测实用手册.北京:中国水利电力出版社,2003
[18]刘珍.化验员读本.北京:化学工业出版社,2004
[19]周群英,李秀兰.分析化学中法定计量单位实用手册.北京:中国计量出版社,2009
[20]张铁垣.化验室工作实用手册.北京:化学工业出版社,2008
[21]李树伟,王照丽.对武汉大学主编分析化学(四版)的看法.大学化学,2002(8)
[22]周宁怀,李俊义,张渔夫.当量浓度的废除与滴定分析的计算.杭州师院学报,1987(1)
[23]McGlashan M. L. International Recommended :Name and Symbols for Physicochemical Quantities and Unit, Ann.Rev.Phys.Chem., 1973(24):51-76
[24]IUPAC Green book, “Qualities, Unites, and Symbols in Physical Chemistry”3rdEdition ,2008
[25]徐斌,齐广才,任乃林.滴定分析结果的一种快速计算方法.延安大学学报,1997(6)
[26]张汝廉.最小公倍数法确定基本单元.郑州工学院学报,1992(1)
[27]李春润.法定计量单位在水质监测与分析中的应用.沈阳化工,1992(4)
[28]陈素娥,池永庆,张树林.滴定分析计算的几点尝试.山西化工,1999(2)
[29]张俊秀.基本单元的确定与等物质量的计算.天津职工大学学报,1995(3)
[30]IUPAC Gold Book, “Compendium of Chemical Terminology”, Version 2.3.1, 2010
[31]李树伟.对武汉大学主编分析化学的几点意见.大学化学,1998(3)

