基于差异化聚类的分级隐私保护数据发布方法

刘海

（浙江金融职业学院经营管理系，浙江杭州310018）

随着计算机技术的不断发展，许多与个体相关的信息在计算机上存储，并且广泛的被应用于大量科学研究领域.这些与个体相关的信息，绝大多数是不需要进行隐私保护的.而需要保护的仅仅是其中一些拥有特殊敏感信息的个体，比如在医疗信息表中，如果某人的疾病是癌症或艾滋病，则对此类个体信息就应该进行保护，而绝大多数人得的是感冒、咳嗽等疾病，个体敏感信息的暴露并不会带来很大的危害性.另一方面，对包含特殊敏感信息的个体，其保护也应具有层次的差别，还是以医疗信息表为例，对某人得的是癌症或艾滋病，因其传染性等诸多不同，我们对其的保护程度也应该有所不同.近年来，隐私保护数据发布也逐渐成为了学术研究的热点，许多学者也提出各种隐私保护数据发布的模型.Sweeney L[1]等早在2002年就提出了利用k-匿名模型来解决隐私保护数据发布相关问题.该模型将数据集分为若干个簇，每个簇中元素至少K个，且簇中元素具有不可区分性.Machanavajjhala A[2]等在2006年于k-匿名的基础上提出了L差异化，该模型要求在每个簇中至少含有L个well-pres⁃ent的敏感属性，通过这种方式解决k-匿名中存在的同质攻击和背景知识攻击的缺陷.Xiao Xiaokui[3]等在2007年提出了面向多次数据发布的隐私保护m-invariance模型，该模型通过保持在在每次数据发布簇中各属性所占比例的不变性来进行隐私保护.Li NingHui[4]等在2007年提出了t-closeness模型，该模型提出每个簇中的敏感元组的分布应该接近于该属性的全局分布.杨晓春[5]等在2008年提出了多维桶模型，并设计了三种优先算法来解决了非单一敏感属性隐私泄露等相关问题.Tiancheng Li[6]在2012年初提出了Slicing模型，其没有明确区分准标识符属性和敏感属性，而是依据属性之间的关系先行切片，切片内属性间关系保持，切片外属性间关系打乱，通过这种方式来处理隐私保护数据发布.

以上的这些模型在一定的领域或范围内也取得了良好的使用效果.本文提出的方法是通过分类、聚集、聚集、泛化的途径.具体上首先将需要保护的敏感元组与大量不需要保护的敏感元组进行分类.然后将不需要保护的敏感元组进行聚集成簇，后测算需要保护的敏感元组与簇之间的距离，将要保护的敏感元组同簇中元组共同泛化，最后通过试验证明，对单一敏感属性的隐私保护该方式也能取得很好的隐私保护效果.

1 相关概念

1）如果QIi[t1]和QIi[t2]为数值型属性，则我们定义该属性之间的距离为：

2）如果QIi[t1]和QIi[t2]为分类型属性，则我们定义该属性之间的距离为：

其中ancestor(QIi[t1],QIi[t2])表示分类树中t1元组的第i个属性和t2元组的第i个属性的最小共同祖先.|Ai|表示分类树的高度.例如在图1中Without-pay和Never-worked的最小共同祖先为Unemployed，而整个分类树的高度为2，故它们之间的距离为0.5.

图1 工作阶层的泛化层次Fig.1 The generation level of workclass

3）σi值依据元组中属性的重要程度不同而分别进行设置.

假设数据集中元组包含n个属性，用QIi[t1]表示元组t1第i个属性，数据集中部分元组已经形成簇集G{C1、C2、…Cn}.则元组t1和簇Cj的距离为：

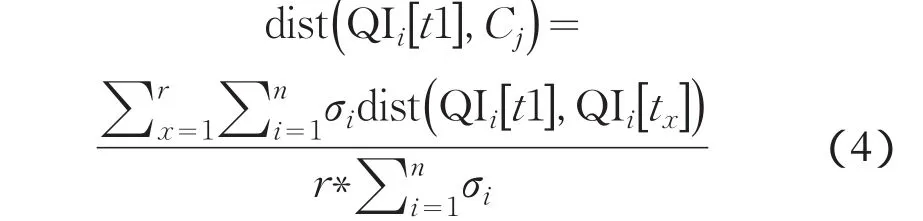
其中r为簇Cj中元组的个数.

2 算法

算法前提：

1）需要保护的敏感属性相对较少，且存在保护级差.

2）敏感属性与准标识符属性之间是可区分的.

3）对每个元组，敏感属性有且只有一个.

4）敏感属性与准标识符属性均不为空.

2.1 算法的三个步骤

第一步Algorithm：Clustering stage

输入：待发布的数据表T（剔除包含重要敏感属性的元组），匿名参数k，权重矢量W.

输出：满足k匿名的数据表PT，及表T中剩余的部分元组.

1）将数据表T中隐匿个体标识属性

2）簇集初始化G=Ø

while（|T|≥2k）do

A.随机选取表T中一个元组ttemp，tfst1=max

k-匿名：给定一数据集，该模型将该数据集划分为若干个簇，使得每个簇中元组个数均大于等于k.簇中元素在准标识符QI上均有相同的属性值.

敏感性分级（ai，k）匿名：给定一匿名表PT，准标识符QI，敏感属性SA，将敏感属性SA按敏感程度分级，并对每个级别的SA满足敏感约束ai，则称该匿名表PT关于准标识符QI及敏感属性集SA满足敏感性分级（ai，k）匿名.

距离度量：数据集中的元组包含数值型属性和分类型属性，计算两元组之间的距离需要分别计算数值型属性之间的距离和分类型数据之间的距离，再将它们恰当的结合起来.

假设数据集中元组包含n个属性，用QIi[t1]和QIi[t2]分别表示元组t1第i个属性和t2的第i个属性，则元组t1和t2之间的距离定义为：(Dis(ttemp,t))，tfst2=max(Dis(tfst1,t)).

B.以tfst1和tfst2为中心查找距离它们最近的k-1个元组，并将这两个簇C tfst1、C tfst2并入簇集G中.

C.T=T-{C tfst1}-{C tfst2}

第二步Algorithm：Adjustment stage

输入：簇集G{C1、C2、…Cx}，及表T中剩余的部分元组.

输出：满足k匿名的簇集G{C1、C2、…Cx}.

While(T!=Ø)

A.随机的从T中任选一个元组t，T=T-{t}.

B.计算距离t最近的簇集，C=min(Dis(t,Ci))，并将t加入到簇集中，C=C∪{t}.

第三步Algorithm：Distribution stage

输入：满足k匿名的簇集G{C1、C2、…Cx}，各类具有分级匿名要求的元组集T*，敏感属性的频率约束a1、a2、...az（z为有敏感属性约束要求的敏感属性个数）.

输出：满足分级匿名模型的数据表PT.

While(T!=Ø)

A.从T*中任选一个元组，计算其到簇集G表中簇集的最近距离簇C=min(Dis(t*,Ci)).

B.假如（簇中该敏感属性个数+1）≤簇中元素个数ai并且簇中元组个数不超过2k，则将该元组加入该簇集.否则G=G-{Ci}反复重新计算最近簇的距离.

依次对簇集中各个簇C中的元组进行泛化，得到满足分级匿名要求的数据表PT.

2.2 算法正确性分析

算法分为三步走，第一步对不包含重要敏感属性的元组依据它们之间的距离进行分类，簇集中的元组数均为k.第二步对剩余的不包含重要敏感属性的元组计算它们和簇集的距离，将它们分别加入到距离其最近的簇集中.通过这两部将非重要敏感属性的元组进行分类，且每个簇集中元组小于2k个.通过第三步将具有分级匿名要求的元组集中元素综合测算其与簇集的距离、计算簇集中元组个数、分级匿名的要求等，将包含重要敏感属性的元组加入到各个簇集当中去.因此该算法是正确的.

2.3 算法复杂度分析

算法第一步对不包含重要敏感属性的元组进行分类，其时间复杂度为：生成第一第二个簇的代价是O（2n+2（k-1）n），生成第三第四个簇的代价是O（2（n-2k）+2（k-1）（n-2k）），生成第五第六个簇的生成.所以算法第一步的平均时间花销为：O（2n+2法第二步，共有X个簇，且每个簇中包含k个元组，因此T中至多有n-xk个剩余元组，对每个剩余元组需计算O（xk），所以共需执行时间为O（（n-xk）（n），算法第三步复杂度也为O（n）.所以总的时间花销为O（O（n2）+O（n）+O（n））=O（n2）.

3 试验及结果分析

3.1 试验数据及参数

试验环境为：Intel Core i5 2.67GHz CPU，2GB RAM，操作系统为Microsoft Windows XP，编译环境是C-FREE 5.0.试验使用Adult标准数据集中的训练数据集，我们首先删除该数据集中Age、Work⁃class、Martial-status、Race、Education属性有为空的元组，其次我们在剩余记录中随机选取5000条记录进行试验.其中以年龄、工作阶层、婚姻状况和种族作为准标识属性，并以Education作为敏感属性进行试验，具体描述见表1.

表1 Adult数据库试验数据描述Tab.1 The data feature of Adult database

试验主要分析基于差异化聚类的分级隐私保护数据发布过程的信息损失和执行时间.我们选取Education属性中的“1st-4th”和“10th”作为需要隐匿的敏感属性，先测算其个数分别为21和133，并预先设置“1st-4th”频率约束a1=1/6,“10th”频率约束a2=1/3.需要隐匿的敏感属性个数概率远小于5000个，具备需要隐匿的敏感属性的特性.我们在两个方面进行比较.

3.2 信息损失量、泛化元组数比较

我们将k值分别取6、12、18、24并分别查看信息总损失量及涉及到的泛化元组数，我们可以看到随着k值的增大，不仅匿名信息的损失总量在增加，泛化的元组数也在增加.这是因为随着k值的增大，在算法第一步中聚类的元组数不断增加，需要保护的敏感属性泛化的元组数同样也增加了.在带来更高隐私保护的同时，匿名信息的损失量也不可避免增加.

3.3 执行时间的比较

我们将k值分别取6、12、18、24并分别查看其算法运行时间，我们可以看到随着k值的增大，执行时间先减少后增加.这是因为随着k值的增大，原先算法第一步执行无须保护元组的聚类所用时间相对在不断减少，而算法第三步将需要保护的敏感属性所在元组聚类到无须保护的元组所在的聚类所用时间不断增加，试验得出在k值为18左右总用时最少.

4 结语

隐私保护数据发布相关热点很多，包括数据集的多次发布、多敏感属性隐私保护、敏感属性动态可变保护、高维度数据保护等一系列隐私保护问题.本文针对单一敏感属性隐私保护相关问题进行研究.通过试验证明该算法能在最大限度保留原有数据属性的同时，通过少量泛化操作来满足不同数据保护度的要求.

[1] Sweenty L.k-anonymity:a model for protecting privacy[J].International Journal on Uncertainty.Fuzziness and Knowledge-based Systems,2002,10(5):557-570.

[2] Machanavajjhala A,Gehrke J,Kifer D.1-Diversity:Priva⁃cy beyond K-anonymity[A].Proceedings Roger S.Barge of the 22nd International Conference on Data Engineering[C].USA:IEEE Press,2006:24-36.

[3] Xiaokui Xiao,Yufei Tao.m-invariance:Towards privacy preserving re-publication of dynamic datasets[A].Lizhu Zhou.Proceedings of the 2007 ACM SIGMOD interna⁃tional conference on Management of data[C].USA:ACM 2007:689-700.

[4] LI N H,LI T C,Venkatasubramanian S.t-closeness:priva⁃cy beyond k-anonymity and l-diversity[A].Adnan Yazi ci.Proceedings of the 23rd International conference on Da⁃ta Engineering[C].USA:IEEE Press,2007:106-115.

[5] 杨晓春,王雅哲,王斌,等.数据发布中面向多敏感属性的隐私保护方法[J].计算机学报,2008,31（4）:574-586.

[6] Tiancheng Li,Ninghui Li,Jian Zhang,et al.Slicing:A New Approach for Privacy Preserving Data Publishing[J].IEEE Trans Knowl Data Eng,2012,24(3):561-574.