基于GIS的城市公交换乘模型与实现

简志伟，冯军锋

(上海市测绘院，上海 200129)

1 引言

城市规模的扩张以及城市人口的增长使得人们在城市中的出行愈发困难，同时也对城市智能交通的信息化程度提出了更高的要求，而加快城市公共交通系统的优化是解决城市人口出行困难问题的重要手段之一。随着城市的发展和科技的进步，城市公共交通不再仅仅由单一的公交车构成，而是集合了公交车、轨道交通、轮渡、索道等众多交通手段的公共交通系统。这在一定程度上提高了乘客的出行效率和选择性，但是，出行手段的多样化使得公共交通系统的复杂性也大大的增加，往往导致公共交通资源的浪费和出行人群在时间、财产上的损失。因此，如何高效的分配公共交通资源是提升城市人群出行效率的关键。

乘客在出行时会主要考虑“换乘次数”、“出行距离”和“出行耗时”这三个方面的因素［1］。传统的公交换乘模型多采用基于数据库的模式［2～4］，通过数据库对公交路线、公交站点及其相关关系进行有效地数据组织，并在此基础上完成公交线路的检索和查询。然而该模型在很大程度上忽视了上述三个影响因素，使得换乘模型与实际出行情况差异较为明显，例如:基于数据库的换乘模型往往忽视了人们能够步行一段距离进行换乘来减少换乘次数的情况，并且无法灵活和准确的计算出出行距离以及在此基础上的出行耗时。而基于GIS的公交换乘模型与传统模型相比，利用GIS在智能交通领域的优势［5］，对公交网络系统和交通网络系统进行GIS数据组织和处理，将属性数据和空间数据有机的结合到一起，不仅可以获取更加符合城市人群实际出行情况的出行线路，还能够在GIS的图形可视化显示这一特点的基础上对选取的线路进行显示，使出行人群对线路的解读更为直观和明了。

公路网络与公交网络的差异［6］决定了解算城市道路网络最短路径的方法并不适用于解算公交网络中的最短路径或最优路径［7，8］，但是道路网络最短路径适用于城市人群在出行时进行站点间换乘的线路选择。因此，本文分别对城市道路网络和城市公交网络进行了GIS抽象，结合图论理论［9］对网络中的各个要素进行了拓扑结构、空间关系、属性关系的表述。在道路网络结构关系完善的基础上采用最短路径算法［10，11］计算城市中任意两站点在城市道路网络中的最短路径，设定弹性的阈值以确定不同的步行换乘距离所对应的换乘路线并将其作为乘客步行换乘时的最优路径。在公交网络结构关系完善的基础上制定公交最优路线选择模型，选择最优的公交线路，并将公交线路与步行换乘线路结合生成最优的出行线路。本文最后结合杭州市的路网和公交等数据进行了试运算，并对结果进行了分析和说明。

2 交通路网与公交网络的GIS数据组织

2.1 公共交通系统要素的GIS表达

城市公共交通系统良好运作的前提是高效的公共交通数据组织和表达。本文对公共交通系统中的各个要素进行了GIS表达，将其抽象为GIS中的“点”要素和“线”要素，并对各要素进行详细描述。

道路的GIS表达主要包括道路节点和道路路段。节点是道路网络中非常重要的一种要素，它是不同路段的相接处，在现实中往往属于城市道路网络中的特征地点［12］。根据需要本文对节点的属性进行组织表达，道路节点的属性主要包括节点编号和节点X、Y坐标，节点编号为该节点唯一标识编号，通过编号可对相应节点进行索引查询;节点X、Y坐标用来标识该节点的绝对位置。路段是对城市中道路的抽象，是城市路网中的“骨架”。单纯采用路段的几何特性对现实道路进行描述并不足以完全表达其特性，更不能满足公交换乘计算的需求，比如计算行车距离需要对乘车路线经过的路段的长度进行求和，因此本文对道路路段的主要属性进行了表述，道路路段的属性主要包括路段编号、路段名称、路段起始节点和终止节点、路段长度等，路段编号为该路段位移标识编号，通过该编号可对相应路段进行索引查询;路段名称为路段所在道路中文名称;路段长度表示该路段实际长度，据此计算线路距离和换乘距离;路段起始节点编号和路段终止节点编号表示连接路段两侧节点的编号，为路段和节点建立索引关系;路段长度标识该路段空间长度。

公交线路的GIS要素包括公交线路、公交站点和公交换乘区。公交线路是公共交通工具在城市道路网络中行驶的路线，它的属性决定了乘客乘车的耗时、距离、花费，如表1公交路线属性中所示，公交线路编号标识公交线路唯一标识，且区分同名线路的不同方向;票价标识乘客乘坐该路公交路线的花费;首班时间和末班时间标识公交线路运行时段，以便为乘客提供准确的公共交通信息。公交站点是公共交通工具在公交线路上行驶的时候停靠的固定点，以满足乘客上、下公共交通工具的需求，如表1公交站点属性中所示，公交站点编号是该公交站点的唯一标识，可以通过编号对站点进行索引查询;公交站点名称表示该站点的中文名称，并不具有唯一性，如相邻反向的一对站点一般均为同名;站点X坐标和站点Y坐标标识公交站点的绝对位置。公交换乘区是乘客进行换乘时在可忍受最大步行距离内能够到达站点的集合。

公共交通网络中的各要素间具有密切的关系，公交换乘区内包含的站点数量主要由乘客所能忍受的最大步行换乘距离以及换乘站点附近的公共交通网络情况决定。如图1所示，该区域中共有3条公交线路，A为某线路中的一个站点，根据设置的最大步行换乘阈值求解站点A的公交换乘区，由图可知，随着最大步行换乘阈值的增大，公交换乘区内包含的站点数量也随之增加，同时，在站点A处可供换乘的公交线路也增加了。

公交路线与公交站点部分属性表 表1

图1 公共交通网络关系图

通过上述过程对城市道路和公交线路的空间数据和属性数据进行组织，为基于GIS的公交换乘模型做好数据准备。

2.2 道路网络与公交网络的表达

城市交通网络作为城市运行的“大动脉”，在城市的发展和建设中起到的作用是不可替代的。交通网络并不是简单的规则网络，而是一个典型的由道路物理网络与交通需求网络结合而形成点－边结构网络，其中道路可以抽象为连线，道路特征点抽象为节点，大量的点和线组成了交通网络构架［13］。城市交通网络主要分为道路网络、公共交通网络、物流网络等，根据基于GIS的公交换乘模型需求，这里只对道路网络和公共交通网络进行表述。

道路网络主要由道路路段和道路节点构成。节点是引起实际道路中断的分界点，表示城市道路属性或交通流在该点发生变化;而路段是由节点截断的城市道路，因此路段与节点的复杂程度决定了道路网络的复杂程度。而城市道路网络作为空间网络具有不同于抽象网络的特性，这些特性决定了城市交通网络的拓扑性质［14］和属性性质。首先，城市道路网络是具有实际意义的网络，并不是抽象出的，路网中的路段都存在与之相对应的现实道路，节点都具有明确的位置，可在现实中找到，如图2(b)所示为某市部分道路网络，其中的路段均具有唯一性且可在现实中图2(a)找到对应的道路;其次，道路节点与路段的连接受到现实道路情况的约束，每个节点连接的路段数是与现实路况相符的，而每条路段的起始位置和终止位置由两个节点确定;再次，现实道路的运行情况决定道路网络的属性，现实道路中存在禁止左行、禁止右行、禁止直行、禁止掉头等情况，这些道路性质决定了道路网络的属性，如图2(a)中的现实道路中存在单行道，则在其道路网络中以禁行标志体现图2(b)。

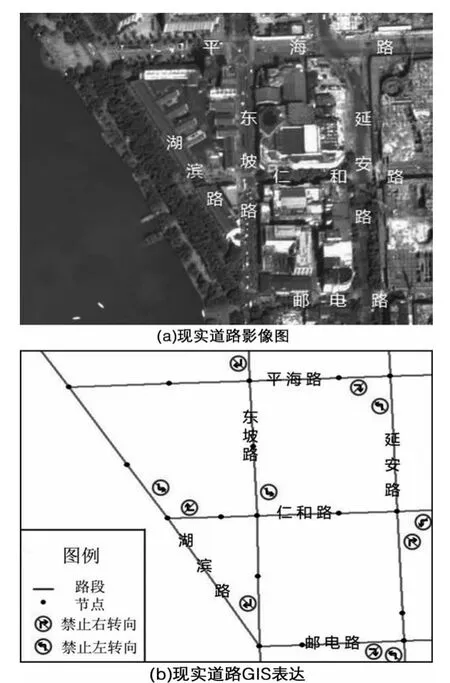
图2 现实道路及属性表达示意图

公交网络是由公交线路、公交站点以及公交换乘区构成的。首先，不同于道路网络，公交网络中的“线”是抽象出的要素，并不能够在现实中明确的找到，而公交站点则是实际存在的地物特征;其次，公交线路具有重合的特点，即不同的公交线路在某个路段内可能发生重合，因此在该路段中的公交线路不具有唯一性;最后，公交站点不存在于公交线路上，并且他们是多对多的关系。

综上所述，城市道路网络与公交网络具有其各自特点，因此，为他们进行高效的逻辑关系组织是实现本文目标的关键。

2.3 公共交通系统要素逻辑关系表达

公共交通系统包括了城市道路网络与城市公交网络以及各要素间的逻辑关系。如图3所示，城市道路网络中要素间的逻辑关系包括:①道路节点标识符具有唯一性，因此可以通过路段的起始节点标识符和终止节点标识符索引到对应节点;②路段具有唯一的起始节点和终止节点，因此通过确定起始节点与终止节点可以锁定唯一路段。城市公交网络中要素的逻辑关系包括:①公交线路的行驶路线决定了经过站点和道路节点的次序;②公交线路与公交站点是多对多的关系;③公交站点与公交换乘区是一对多的关系，换乘区内站点数量与换乘站点位置及其周边路网状况相关，一个站点的换乘区至少包含其自身。本文中公交线路与节点、站点通过公交线路－站点－节点索引建立逻辑关系。公交线路－站点－节点索引中设置公交线路标识符以检索公交线路，设置换乘矩阵检索换乘站点的公交换乘区，设置站点、节点出现在指定公交线路中的次序索引以确定公交线路运行方向，设置节点标识符和站点标识符检索道路节点与公交站点。

图3 道路网络与公交网络逻辑关系图

通过上述的逻辑关系组织建立公交线路与站点、公交线路与节点、公交线路与路段等不同要素间的相关关系，基于上述相关关系在换乘模型中通过已知要素检索其他要素的空间信息和详细属性信息。

3 基于GIS的公交换乘模型

基于GIS的公交换乘模型包括换乘矩阵模型和公交线路查询模型。通过换乘矩阵模型求解站点在指定阈值内的公交换乘区，同时在道路网络数据、公交网络数据以及求解得到的公交换乘区的基础上通过公交线路查询模型求解公交线路。

3.1 换乘矩阵模型

本文通过换乘矩阵记录各站点的公交换乘区。定义换乘矩阵的行名和列名均为公交站点的编号，矩阵的元素为0或1。如表2所示，若两站点间存在换乘关系则其对应元素设为1，反之则设为0。显然，因为同站与其自身必定具备换乘关系，所以换乘矩阵对角元素均为1，且换乘矩阵是一个对称阵，所以将其存储结构设定为半角矩阵。

换乘矩阵是由两个要素确定的:

(1)两站点间的距离:

城市中两站点的距离可分为空间距离和道路网中的最短路径。两站点的空间距离可认为是两点间的直线距离;两站点间的最短路径可由Dijkstra算法［15］求解得到。

本文采用两站点在城市路网中的最短路径来计算换乘矩阵。很多情况下，人们步行换乘的路线并不是直线，因而采用两站点空间距离计算换乘矩阵会产生数据不精确甚至数据错误的可能性，例如:某两站点空间距离小于乘客可忍受的步行换乘距离，但是因为两站点间有障碍物阻挡，乘客换乘必须绕行较远距离，此时若设定这两个站点存在换乘关系则会误导乘客，给乘客的出行带来不便。而城市路网中两点间的最短路径则是道路网络中由出发点到目标点实际存在的线路，且换乘矩阵所标识的具有换乘关系的两个站点必定存在小于乘客可忍受步行换乘距离的路线，所以采用最短路径计算明显更加符合实际情况。

(2)乘客可以忍受最大步行换乘距离dmax:

不同乘客可以忍受的最大步行换乘距离一般是不同的，因而对于不同的乘客换乘矩阵是不同的。本文通过设定 300 m、500 m、800 m三种不同的阈值dmax计算了得到了 300 m换乘矩阵、500 m换乘矩阵和800 m换乘矩阵来满足不同乘客的出行需求。

根据上述两要素最终可由下列公式确定换乘矩阵:

其中hij为换乘矩阵中第i行第j列的元素，dij为编号为i的站点和编号为j的站点间的最短路径，dmax为计算换乘矩阵设定的阈值，n为城市路网中公交站点数。

3.2 换乘时间模型

公交路线的确定离不开时间这个重要的参数，往往大型城市的公共交通网络中存在上百条公交线路，不同公交线路的始发和结束时间，时间间隔都不一定相同。因此，时间因素需要作为一个重要参数放入换乘模型中进行考虑。

本文通过在公交线路数据中设置首班车时间、末班车时间以及发车间隔，使换乘模型更为准确和符合实际。乘客在查询路线时可以选择将乘坐时间输入，模型将乘客乘坐时间作为可选参数在数据库中进行选择，保留符合乘客乘坐时间的线路。

3.3 公交线路查询模型

本文针对复杂的轨道交通网络、丰富的公交资料结合基础地理信息重新设计更为合理的公交换乘算法模型，使其同时为最优推荐，即直达车优先考虑，其他方案根据经验公式综合评估步行距离、总里程、换乘次数、公交类型等因素进行筛选的原则提供查询结果。如何设计模型、测算经验公式使其更合理、高效提供方案是关系到本系统实用性的最主要因素。

公交换乘模型建立在城市道路网络的GIS表达、城市公共交通网络的GIS表达以及公交换乘矩阵上，模型算法思路是:根据城市道路网络的GIS表达和城市公交站点的GIS表达解算出不同阈值下的换乘矩阵并将其录入数据库;根据起始站点和终止站点检索公交站点的GIS表达，寻找站点唯一编号后结合公交路线的GIS表达和公交换乘矩阵依次进行直达路线检索、一次换乘路线检索和两次换乘路线检索，考虑到计算效率和实际乘车情况，3次及3次以上换乘路线被视为不可到达。

公交路线查询模型具体分为:

(1)直达线路查询模型如图4所示。

图4 直达线路查询模型图

(2)一次换乘线路和两次换乘路线查询模型，如图5、图6所示。

图5 一次换乘线路查询模型图

图6 两次换乘线路查询模型

4 城市公交换乘实例分析

为了验证算法的可靠性以及效率，本文采用杭州市的城市道路网络数据和城市公共交通网络数据进行验证。实例选取杭州市区西北侧的“大关山站”为起始站点，杭州市区东南侧的“新街站”为目的地站点，换乘时间设定为夜间10时，换乘阈值设定为 500 m进行测试。该实例的选取跨越杭州市区，属于远距离的公交线路查询，具有典型性。

图7 公交路线查询实例图

查询结果如图7所示，路网中的点表示公交站点，加粗实线表示查询得到的公交线路，图右侧为乘客在中转站进行步行换乘的线路，虚线表示乘客步行换乘的路线。结果表明全程共需要进行两次换乘到达目的地，总行程长度约为 32.3 km，具体路线为:

(1)从大关山站乘坐K348路公交车，行驶55站约 22.9 km到武林门北站下车;

(2)从武林门北站步行约 358 m到武林门湖墅路口站;

(3)从武林门湖墅路口站乘坐K106路公交车，行驶14站约 7.1 km到总管塘站下车;

(4)从总管塘站换乘K520路公交车，行驶15站约 2.3 km到终点站新街站下车。

根据上述结果可以发现，通过设定步行换乘的最大阈值，乘客在出行过程中需要步行换乘的最大距离为 358 m，经过两次换乘后到达目的地，完全符合乘客设定的需求。

5 结论

随着中国经济的迅速发展，作为区域经济中心的城市扩张是在所难免的，而伴随而来的问题也与日俱增，包括城市居民出行在内的所有问题都面临着新的挑战。因此，不断探索解决问题的新方法是城市居民正常生产生活的保障。本文结合地理信息系统在解决空间数据方面的优势和传统的基于数据库的公交换乘模型在解决属性数据方面的优势，提出了基于GIS的公交换乘模型，经过测试显示，换乘模型能够满足对步行换乘距离有要求的乘客的需求，并对查询结果采用可视化显示和文字说明结合的方式，使公交路线更为直观和明了。

［1］ 杨新苗，王炜，马文腾等.基于GIS的公交乘客出行路径选择模型［J］.东南大学学报:自然科学版，2000，30(6): 87～91.

［2］ 王建林.基于换乘次数最少的城市公交网络最优路径算法［J］.经济地理，2009，25(5):673～676.

［3］ 王庆平，张兴芳，宋颖等.城市公交换乘的数学模型及其算法实现［J］.计算机工程与应用，2008，24(7):246～248.

［4］ 张林峰，范炳全，吕智林.公交网络换乘矩阵的分析与算法［J］.系统工程，2003，21(6):92～96.

［5］ 李曙光，苏彦民.基于GIS的城市公交路网的最优路线算法研究［J］.中国公路学报，2003，16(3):83～86.

［6］ 赵月，杜文，陈爽.复杂网络理论在城市交通网络分析中的应用［J］.城市交通，2009，7(1):57～65.

［7］ W SC，T CO.Estimation of time－dependent origin－destinationmatrices for transitnetwork［J］.Transportation Research Part B，1998，32(1):35～48.

［8］ 何迪，严余松，郭守儆等.基于矩阵分析的公共交通网络最优路径算法［J］.西南交通大学学报，2007，42(3):315～319.

［9］ 王杰臣，毛海城，杨得志.图的节点－弧段联合结构表示法及其在GIS最优路径选取中的应用［J］.测绘学报，2000，29(1):1～5.

［10］ 严寒冰，刘迎春.基于GIS的城市道路网最短路径算法探讨［J］.计算机学报，2000，23(2):210～215.

［11］ 张福浩，刘纪平.一种基于Dijkstra的海量空间数据最短路径算法［J］.辽宁工程技术大学学报·自然科学版，2009，28(4):554～557.

［12］ 邬伦，刘瑜，张晶等.地理信息系统－原理，方法和应用［M］.北京:科学出版社，2009:134～176.

［13］ 吴建军，李树彬.基于复杂网络的城市交通系统复杂性概述［J］.山东科学，2009，22(4):68～73.

［14］ 徐建华.现代地理学中的数学方法［M］.北京:高等教育出版社，2002:259～273.