新型耐高温光纤光栅温度传感器

张智禹，于文革

(沈阳航空航天大学，辽宁沈阳　110136)

0　引言

光纤光栅作为一种新型的光纤无源器件，因其具有抗干扰性强、耐腐蚀、体积小、重量轻、寿命长、无连接损耗、可实现多点分布式测量等优良特性，在光传感领域具有广阔的应用前景[1]。普通I型光纤光栅只适用于200℃以下的工作环境[2]，当温度高于200℃时其反射率随温度的上升而下降，300℃时产生衰退效应。Ⅱ型光纤光栅[3]、ⅡA型光纤光栅[4]、化学组分光纤光栅(CCG)[5]、掺杂特殊离子的光纤光栅[6]等耐高温光纤光栅由于制作成本高昂，制作工艺复杂限制了其应用。 I型光纤光栅传感器通常只适用于常温测量，其高温测量主要受两方面原因限制：(1)封装材料限制。光纤光栅温度传感器封装材料主要是热膨胀系数大的聚合物，但是环氧树脂胶其使用温度工作温度为-50～+180℃[7]，硅橡胶在150℃下其物理性能基本不变，在200℃下可长期使用[8]；(2)本身衰退性质限制[9]。以上两方面限制了光纤光栅在高温环境下的使用，如何实现光纤光栅高温测量已然是国内外研究的热点话题。

文中利用绝热材料对栅区进行封装，用热膨胀系数大的铝棒作为受热材料。把传感器放置于高温环境中时，铝棒受热膨胀对外产生外力，该力通过杠杆结构，在光栅端放大，使光栅发生变化，以达到对高温的测量效果。

1　光纤光栅传感原理的介绍

光纤光栅的中心反射波长为[10]：

λB=2neffΛ

(1)

式中：neff为有效折射率；Λ为光栅周期。

可见Bragg波长λB随neff和Λ的变化而变化，而neff和Λ的改变与应变和温度有关。应变和温度分别通过弹光效应与热光效应影响neff，通过长度改变和热膨胀效应影响Λ，进而使λB发生移动。

光纤Bragg光栅的反射峰值可以近似等于λB，可表示为应变和温度的函数

λB=2neffΛ=2neff(ε，T)Λ(ε，T)

(2)

对式(2)全微分，整理得，

(3)

根据应变、热膨胀系数和热光系数的定义可知折射率和应变、温度的关系为，

(4)

式中μ为泊松比；P1i是光弹性张量的普克尔压电系数；P为有效弹光系数；ξ为热光系数，它们是与光纤材料有关的常数；ε为轴向形变；ΔT为温度变化量，℃。

周期和应变、温度的关系为，

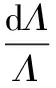
(5)

式中，α为热膨胀系数，是一个与光纤材料有关的常数，对掺锗石英光纤，其一般取0.55×10-6。

Bragg波长与应变和温度的关系为

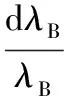
(6)

可以看出，温度和应力都能导致FBG中心波长产生变化。

2　温度传感器的设计

2．1温度对物体热膨胀的影响

热膨胀是由温度变化而引起材料尺寸和外形的变化。通常材料受热时均会膨胀。热膨胀主要分为线性膨胀，面膨胀和体膨胀[11]。

体膨胀系数β或线膨胀系数α的定义为一定压力P下物体体积V或长度L随温度T的变化率。公式表示为：

(7)

(8)

对于各向同性材料，β=3α．

只考虑材料的线膨胀，当压力P一定时，可由式(8)得，

(9)

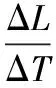
(10)

式(10)表示每变化1 ℃长度L物体的增加量为αL．由式(10)可知，

(11)

即当温度变化时应变量为ε=αΔT．

2．2温度传感器设计结构

传感器的结构如图1所示，光纤通过固定支架8，固定在8的上端。FBG由绝热材料封装，光纤的另一端固定在滑块7上，滑块7可以在固定支架8上滑动，光栅紧紧贴在固定支架8上，杠杆6的一段固定在滑块7上，4为杠杆的支点，另一端固定在铝棒5上，杠杆6的前端(滑块7到支点4)长度l2小于后端(支点4到铝棒5)长度l1。当外界温度变化时候，铝棒5受温度影响发生形变从而产生力，推动杠杆运动。通过杠杆使滑块7产生的轴向拉力，由此起到增敏作用。由于光栅不受温度影响，避免了在高温环境中的衰退效应，因此可以测较高的温度。

1—光纤；2—胶；3—FBG；4—支点；5—铝棒；6—杠杆；7—滑块；8—支架。

2．3传感器理论分析

当铝棒受热膨胀时，产生外力并作用于杠杆上，使杠杆发生弯曲产生挠度，铝棒受热膨胀长度变化量和杠杆挠度之间的关系为[12]，

(12)

式中：F为铝棒受热产生的力；l1为杠杆的铝棒到支点间的长度；I为杠杆的惯性矩，I=πd4/64；d为杠杆的直径；l为铝棒长度；A铝为铝棒的横截面积；α为铝棒的热膨胀系数；ΔT为温度变化量。

由式(12)可知第二项要比第一项小4～5个数量级，故可以舍去。所有铝棒受热膨胀产生的力为，

(13)

由杠杆原理可知，光纤光栅端产生的拉力为

(14)

由应变公式，可以得到作用力F′和应变的关系为，

(15)

式中：E为光纤的杨氏模量；l2为杠杆的光纤端到支点的长度；A为光纤的横截面积。

由于光纤光栅不受温度影响，故式(6)改为

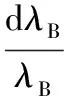
(16)

把式(15)代入式(16)可得波长变化和温度的关系

(17)

2．4实验

实验所用光纤光栅中心波长1 570 nm，反射率大于85%，其杨氏模量E=70 GPa，解调仪的分辨率为 1 pm．室温为21℃，并不发生变化。l1长为5 cm，l2长为25 cm，l2/l1=5，铝棒l长为10 cm，直径为12 mm．杠杆为直径5 mm的不锈钢棒，其杨氏模量E杠=206 GPa．

实验装置如图2。将封装好的光纤光栅放入可控温箱中，宽带光源ASE发出的光经3dB耦合器入射到光纤光栅中，被反射后又经3dB耦合器送到光谱分析仪OSA，通过光谱分析仪观察光纤光栅反射峰中心波长的变化。加温试验采用逐步升温法，由室进行升温实验21℃升至310℃，每次升温幅度为10℃，并通过温度计进行校正，以减小可控温箱的误差。升温间隔为5 min，待波长稳定后，保留数据。重复此过程一直测到310℃。并以相同的方法测量降温的过程。测量数据如表1所示。

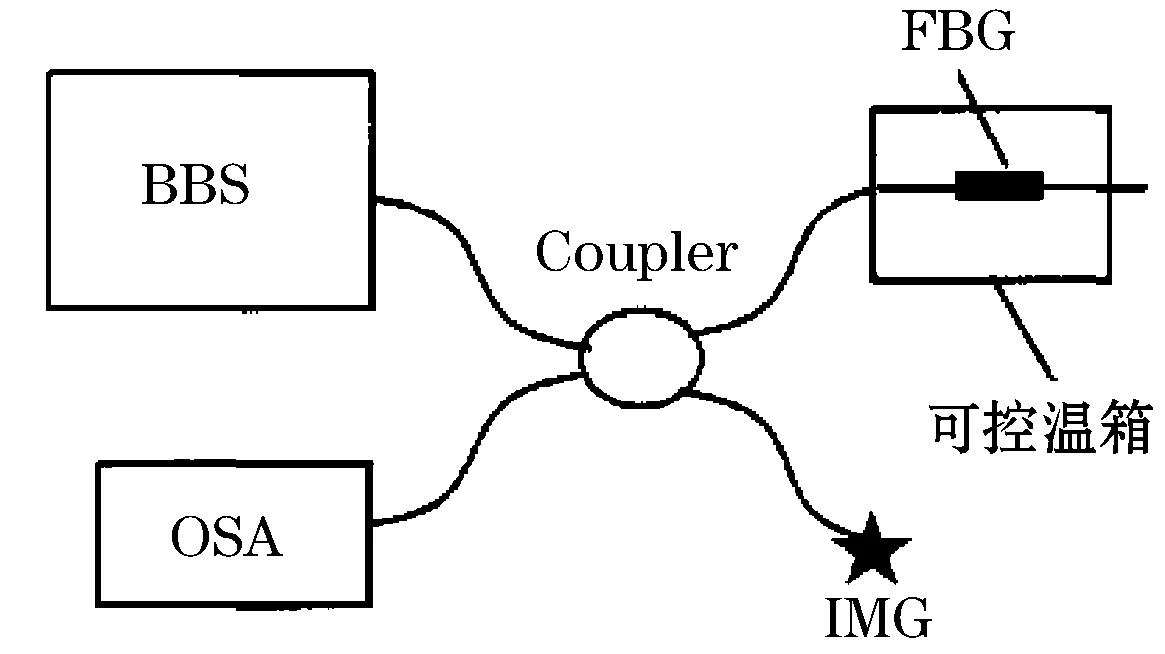
图2　实验原理图

2．5实验数据分析

将实验设备数据带入式(17)中可得该传感器的波长变化和温度的关系为，

表1　测量数据

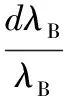
(18)

由式(18)可知该传感器的温度灵敏度系数的理论值是13.11×10-6/℃，大约是裸光纤的1.82倍(裸光纤的温度灵敏系数为7.2×10-6/℃)，即此结构温度每变化1℃中心波长变化量为20 pm．

通过表1可知中心波长和温度的关系如图3所示。

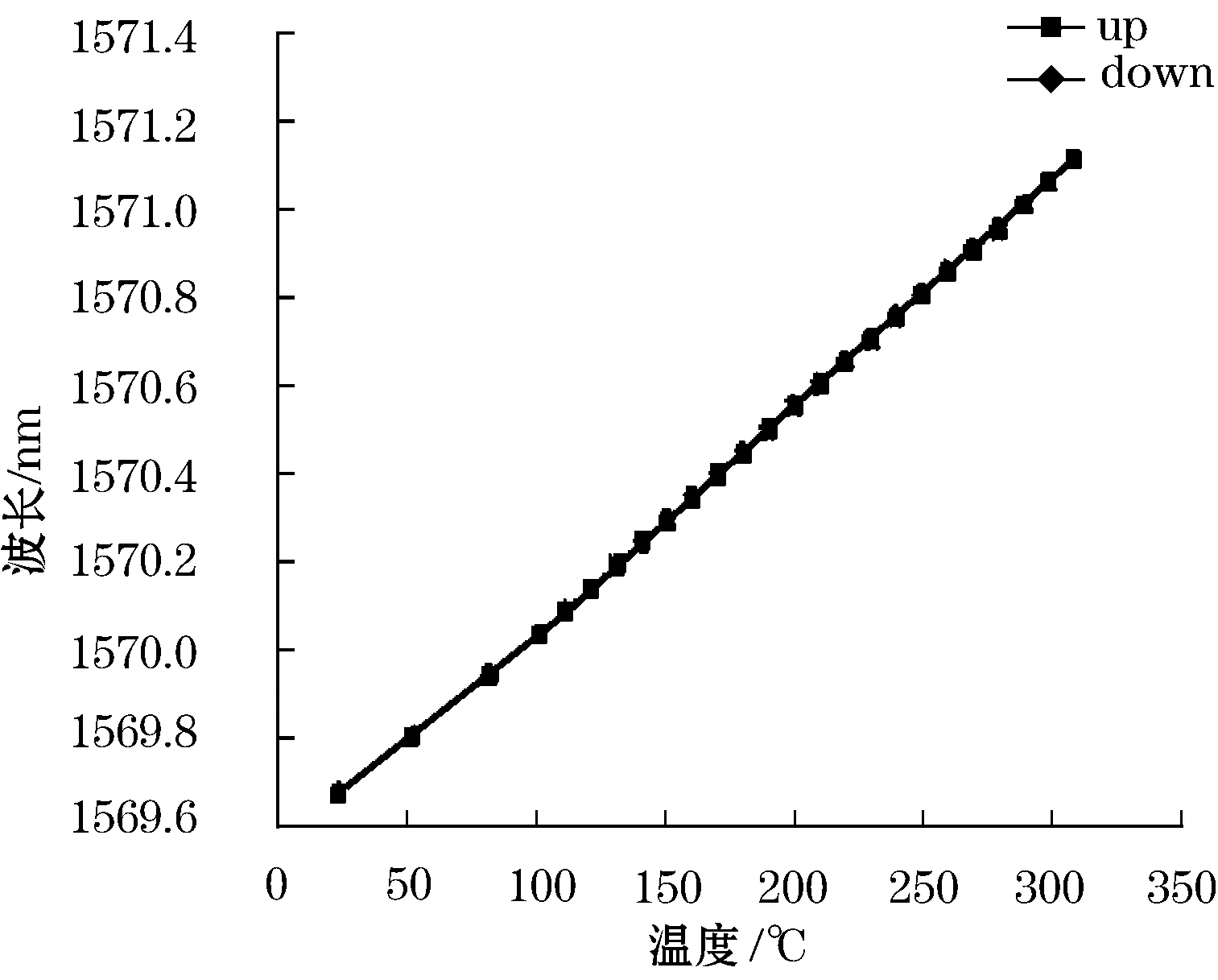
图3　波长和温度变化图

图3可以看出中心波长和温度具有良好的线性关系，其线性方程为y=0.005x+1569.636，用origin对表1中数据进行分析其线性拟合度r2=0.9993，并且没有延迟现象。此传感器的温度灵敏度为0.005 nm/℃，是裸光纤的0.5倍(裸光纤的温度灵敏度为0.010 nm/MPa)。

3　结束语

为了提高光纤光栅温度测量范围，设计了一种新颖结构的耐高温传感器。对栅区进行绝热封装，使其即避免了在高温环境中产生衰退效应也避免了有机物封装的局限性，从而实现该传感器对高温的测量。由铝棒感受外界温度变化，再通过杠杆对产生的力进行增敏作用。实验测得侧传感器的温度灵敏度为0.005 nm/℃，测量的温度高达310℃，并且保持良好的线性。此结构优点为：(1)能够有效的消除外力对光纤光栅的影响；(2)光栅被绝热材料封装，本身不受温度的影响，避免了衰退效应(3)通过杠杆对作用力增敏作用(4)无聚合物封装，可实现高温测量。

参考文献：

[1]姜德生，何伟．光纤光栅传感器的应用概况．光电子，2002(4)．

[2]BAKER S R，ROURKE H N，BAKER V，et al．Thermal decay of fiber Bragg gratings written in boron and germanium codoped silica fiber．J．Lightwave Technol．，1997，15(8)：1470-1477．

[3]ARCHAMBAULT J L，REEKIE L，RUSSELL P S J．100%reflectivity Bragg reflectors produced in optical fibres by single excimer laser pulses．Electron．Lett．，1993，29(5)：453-455．

[4]NIAY P，BERNAGE P，LEGOUBIN S，et al．Behavior of spectral transmissions of Bragg gratings written in germania-doped fibers：writing and erasing experiments using pulsed or cw uvexposure．Opt．Commun．，1994，113(1-3)：176-192．

[5]FOKINE M．Formation of thermally stable chemical composition gratings in optical fibers．J．Opt．Soc．Am．B．，2002，19(8)：1759-1765．

[6]DONG L，CRUZ J L，REEKIE L et al．Enhanced Photosensitivity in Tin-Codoped Germanosilicate Optical Fibers．IEEE Photon．Technol．Lett．，1995，7(9)：1048-105．

[7]陈平，刘胜平．环氧树脂．北京：化学工业出版社，1999．

[8]杨洪，申屠宝卿．硅橡胶的耐热稳定性．合成橡胶工业，2005，28(3)：229-233．

[9]刘钦朋．光纤光栅高温高压传感技术研究．2007(5)：15．

[10]杨立．钢筋腐蚀光纤光栅传感器设计与封装．2009(3)：1．

[11]江磊，沈烈，郑强．聚合物的热膨胀．功能材料，2004(2)．

[12]闫晓鹏，武瑛．材料力学．北京清华大学出版社，2013．