LMD形态学与EEMD形态学在故障诊断中的对比研究

侯高雁，吕　勇，李友荣，王志刚

(武汉科技大学机械自动化学院，湖北武汉　430081)

0　引言

针对非线性非平稳信号中故障频率特征的提取，人们研究了很多种方法，如希尔伯特变换、小波变换和数学形态学等。Hilbert-Huang变换，由于Hilbert算子不可避免的加窗效应，使得解调结果出现非瞬时相应特性，增大解调误差；小波变换中小波基的选择方面是一个难点，同时也存在傅里叶变换的局限性；数学形态学[1]是由法国数学家Matheron G和Serra共同创立的一种不同于时域和频域的数学方法。该方法采用结构元素探针，在信号中不断移动，来提取有用信号的冲击特征，但是滤除白噪声的能力却不足。针对这一不足，研究了总体经验模式分解(EEMD)降噪和局域均值分解(LMD)降噪，并对二者进行了比较。

EEMD是Wu等[2]提出的一种将噪声辅助分析用于经验模式分解(EMD)中的自适应分析方法，该方法克服了EMD[3]产生的混叠现象。LMD是Jonathan S．Smith[4]提出的一种自适应非平稳信号处理方法，该方法不仅分解速度快，而且能够很好地抑制端点效应。

1　数学形态学

数学形态学分析是基于积分几何和随机集的不同于时域、频域分析的非线性方法。该方法首先应用于图像处理中，随后在信号处理方面得到了广泛的应用[5]。它是使用结构元素探针在信号中不断移动来提取有用信息，进行特征分析和描述。

1．1数学形态学基本运算

数学形态学包括2种基本算子[6]：膨胀和腐蚀。设f(n)和g(n)分别为定义在F={0，1，2，…，N-1}的一维多值信号和G={0，1，2，…，M-1}的一维结构元素序列，其中N和M都是整数，且有N≥M．

则f(n)关于g(n)的膨胀、腐蚀、开运算和闭运算分别定义为：

(f⨁g)(n)=max{f(n-x)+g(x)；x∈G}

(1)

(fΘg)(n)=min{f(n+x)-g(x)；x∈G}

(2)

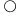
(3)

(f·g)(n)=(f⨁gΘg)(n)

(4)

式中：⨁为膨胀运算；Θ为腐蚀运算；o为开运算；·为闭运算。

1．2形态学滤波器

形态学滤波器开运算用于抑制正冲击，平滑负冲击；腐蚀运算用于平滑正冲击，抑制负冲击；开运算可以抑制边界上的毛刺(凸起部分)，消除比结构元素小的孤点、碎线和斑块；闭运算可填补边界上的凹陷部分，弥合裂缝，填充小洞，平滑外边缘。

基于形态学开运算和闭运算，可以构建2种滤波器，平均滤波器(AVG)和差值滤波器(DIF)。

平均滤波器公式为

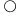
(5)

差值滤波器公式为

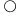
(6)

平均滤波器用于消除信号中的正、负冲击，对信号起到平滑作用；差值滤波器用于提取信号中的正、负冲击。

1．3形态学结构元素

形态学滤波器所选用的结构元素起着至关重要的作用。结构元素的特征包括其形状、高度和宽度，常用的形状有余弦、三角、半圆和直线等，选择了结构元素的形状后，结构元素的高度和宽度就是影响滤波效果的关键因素。大量研究表明：结构元素越复杂，宽度越大，其提取信号的效果也越好，但同时计算耗时也越长。在实际应用中，结构元素应尽可能小并接近待处理信号特征。

2　EEMD形态学

2．1EEMD基本原理

EEMD是针对EMD存在的模式混叠缺陷而提出的改进方法。EEMD方法的核心思想是在采集信号中加入特定的高斯白噪声，将使信号在不同时间尺度上具有连续性，不仅信号极值点的特性发生了变化，而且还提高了抗混分解，有效地避免了模式混叠现象。

EEMD分解过程如下[7]：

(1)在目标信号x(t)中N(N>1)次加入均值为0，标准差为常数的高斯白噪声ni(t)(i∈(1，N])，得到y(t)信号。

yi(t)=x(t)+ni(t)

(7)

(2)对yi(t)进行EMD分解，得到各个IMF分量，记为Cij(t)，余项为ri(t)。其中，Cij(t)表示第i次加入高斯白噪声后，分解得到的第j个IMF分量。

(3)运用统计学原理将得到的IMF分量进行总体平均运算，以消除多次加入高斯白噪声对真实IMF的影响，最终得到的IMF为

(8)

式中cj(t)为目标信号进行EEMD分解后的第j个IMF分量。

2．2基于EEMD的形态学

将目标信号首先进行EEMD降噪，选取主要信息IMF分量重构，然后用形态学差值滤波器来提取故障频率特征。采用EEMD降噪，添加的白噪声为分析信号提供了均匀分布的分解尺度，同时也平滑了脉冲干扰，使得脉冲干扰在分解过程中混入到白噪声模式，抑制了脉冲干扰和模式混叠现象，得到物理意义更明显的IMF分量，更有利于故障特征的提取。

3　LMD形态学

3．1LMD基本原理

LMD的实质就是将非平稳调制信号分解成一系列PF分量，每个PF分量由1个包络信号和1个纯调频信号的乘积而得，对于原始信号x(t)，LMD分解具体步骤如下[8]：

(1)找出x(t)所有局部极值点ni，由式(9)和式(10)分别计算出相邻两极点的平均值mi和包络估计值ai：

(9)

(10)

然后分别将所有相邻的均值点mi和包络函数值ai用直线连接，用滑动平均法进行处理，分别得到局部均值函数m11(t)和局部包络估计函数a11(t)。

(2)将光滑的局部均值函数m11(t)从原始信号x(t)中分离出来，并用光滑的局部包络估计函数进行归一化操作：

h11(t)=x(t)-m11(t)

(11)

(12)

对s11(t)重复上述步骤便能得到s11(t)的包络估计函数a12(t)。若s11(t)在区间[-1，1]上不是一个纯调频信号，则将s11(t)作为原始信号重复n次步骤(1)操作，直至s11(t)为一个纯调频信号。

(3)将所有局部包络估计函数相乘便得瞬时幅值函数：

(13)

而首个乘积函数可得到第一个PF分量PF1。

PF1(t)=a1(t)s1n(t)

(14)

(4)将第1个PF分量从原始信号中分离出来：

u1(t)=x(t)-PF1(t)

(15)

得到一个新的信号u1(t)，将u1(t)作为原始信号重复上述步骤(1)～(3)k次，直到uk为一个单调函数为止。

经过上述步骤，初始信号x(t)被分解为k个PF分量和uk(其中uk为残余项)之和，即：

(16)

3．2基于LMD的形态学

在提取特征频率之前，先进行LMD降噪，将能量高的PF分量重构，再用形态学差值滤波器进行解调，提取出故障频率特征。该方法计算时间短，降噪效果好，能够快速、准确地从故障信号中提取出故障频率特征。

4　EEMD形态学与LMD形态学对比

基于EEMD形态学和基于LMD形态学都能够从故障信号中提取出故障频率特征，然而两者却存在着差异性，从理论上讲，LMD方法减少了迭代次数，分解速度远快于EEMD分解；LMD与EEMD都具有端点效应，但是LMD方法抑制端点效应方面要优于EEMD。通过仿真试验和齿轮故障模拟实验具体来体现两种方法的优劣。

4．1仿真试验对比

采用的仿真信号为

y(t)=x1(t)+x2(t)+x3(t)

(17)

式中：x1(t)为频率为30 Hz和50 Hz的谐波信号，x1(t)=1．2cos(2·pi·30·t)+1．6cos(2·pi·50·t)；x2(t)为标准差为1的高斯白噪声；x3(t)为频率为20 Hz，周期内冲击函数为exp(-20t)sin(20·pi·t)的周期性指数衰减冲击信号；采样频率为1 000 Hz；采样时间为2 s．

此实验是为了抑制白噪声和谐波信号，来提取频率为20 Hz的冲击成分，得到的仿真信号如图1所示，图2为仿真信号的频谱图，只能看到频率为30 Hz和50 Hz的谐波信号。

图1　混合信号的时域图

图2　混合信号的频域图

分别采用上述两种方法对仿真信号y(t)进行处理，得到的结果如图3所示。图3(b)是LMD形态学处理后的结果，图3(b)与图3(a)相比，都可以明显提取出20 Hz的冲击成分，并且其2倍频、3倍频信号也比较明显，但是LMD的分解速度远远大于EEMD分解速度，此外，提取到的1倍频和2倍频的幅值要略比图3(a)提取到的高。图3(a)提取到的1倍频和2倍频幅值为0．074 54 V和0．010 63 V；图3(b)提取到的1倍频和2倍频幅值为：0．091 68 V和0．013 23 V.所以LMD形态学提取到故障频率特征的效果要优于EEMD形态学。

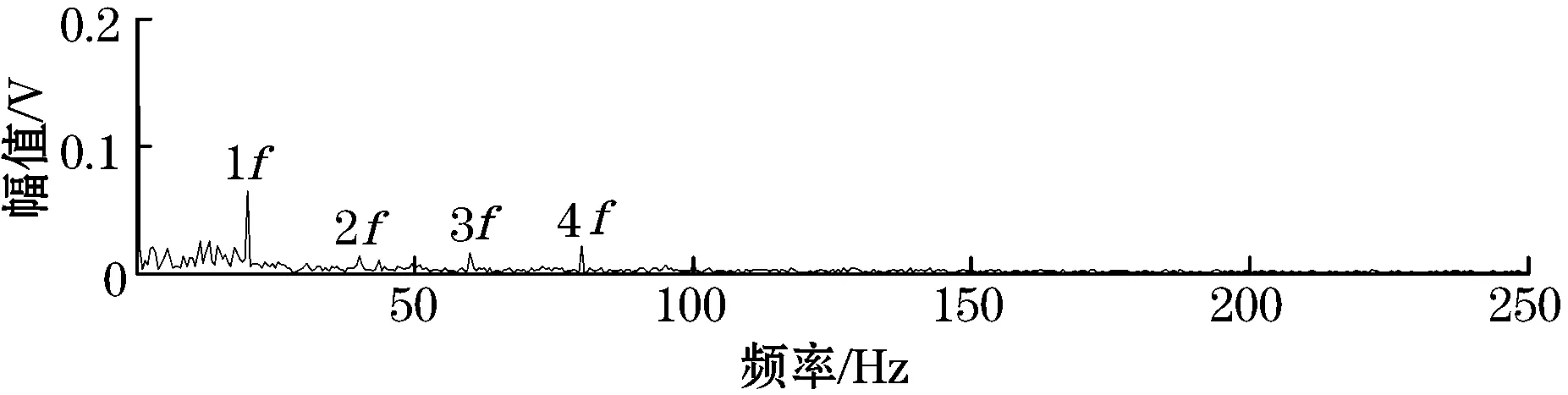
(a)EEMD形态学处理后的结果

(b)LMD形态学处理后的结果

4．2齿轮故障实验对比

通过齿轮断齿和磨损2种故障来比较2种方法。在齿轮箱故障诊断试验平台上进行实验，齿轮箱为1级降速传动，输入轴转速为363 r/min，大齿轮和小齿轮的齿数分别为37和20，模数为3，传动比为1．85，采样频率为2 kHz，采样时间为1 s．图4(a)为齿轮断齿信号的时域图；图4(b)为齿轮磨损时域图。

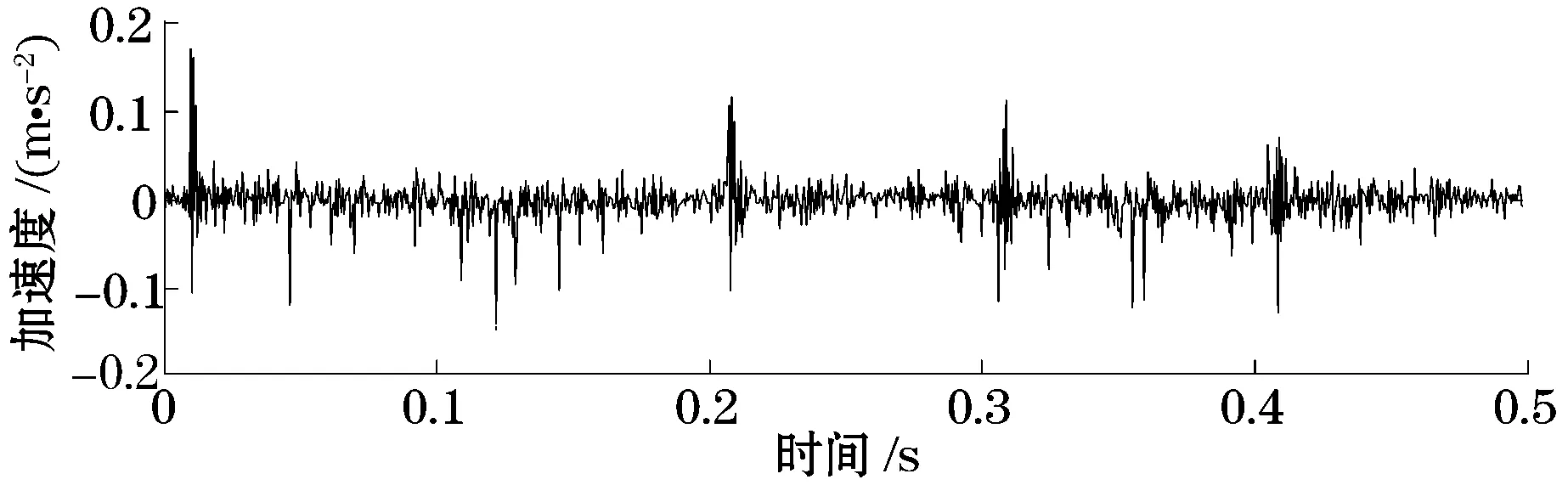
(a)齿轮断齿信号的时域图

(b)齿轮磨损时域图

断齿信号经过2种方法处理后的结果如图5所示。图5(b)与图5(a)相比，LMD形态学要优于EEMD形态学。

(1)2种方法均可以明显提取到断齿的故障频率特征及其倍频信息；

(2)图5(b)中故障频率的幅值要比图5(a)的高，提取出的效果更好；

(3)图5(b)还可以明显的看到故障频率的1/2倍频信息。

(a)EEMD形态学处理后的结果

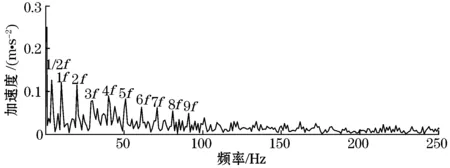
(b)LMD形态学处理后的结果

将磨损信号也经过2种方法的处理，得到图6所示结果。

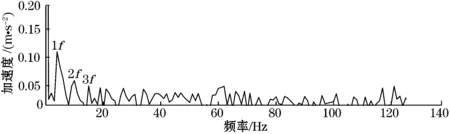
(a)EEMD形态学处理后的结果

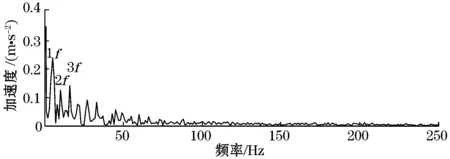
(b)LMD形态学处理后的结果

两者比较可得，采用LMD形态学方法提取到的故障频率特征比较明显，并且噪声能量比较低缓，其倍频信号和倍频的幅值都优于EEMD形态学。

5　结论

基于EEMD的形态学和基于LMD的形态学都能够提取到故障信号的故障频率特征，为故障诊断做好准备，通过理论分析、仿真试验和齿轮模拟故障实验，结果表明LMD形态学在提取故障频率特征方面要优于EEMD形态学，结论如下：

(1)LMD形态学较EEMD形态学减少了迭代次数，分解速度远大于EEMD，并且抑制端点效应也优于EEMD形态学；

(2)提取到的故障频率及其倍频信息，LMD形态学的效果要比EEMD形态学更清晰。

参考文献：

[1]SERRA J．Morphological filtering：an overview．Signal Process，1994，38(4)：3-11．

[2]WU Z，HUANG N E．A study of the characteristics of white noise using the empirical mode decomposition method．Proc．R．Soc．1Dndon A，2004，460：1597-1611．[3]HUANG N E，SHEN Z，LONG S R,et al．The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis．Proc．R．Soc．Lond．A，1998，454：903-995．

[4]SMITH S J．The local mean decomposition and its application to EEG perception data．Journal of the Royal Society Interface，2005，2(5)：443-454．

[5]李兵，张培林，米双山，等．机械故障信号的数学形态学分析与智能分类．北京：国防工业出版社，2011．

[6]罗洁思，于德介，彭富强，等．基于EMD的多尺度形态学解调方法及其在机械故障诊断中的应用．振动与冲击，2009，28(11)：84-86．

[7]陈仁祥，汤宝平，马婧华，等．基于EEMD的振动信号自适应降噪方法．振动与冲击，2012，31(15)：82-86．

[8]程军圣，杨怡，杨宇，等．基于LMD的能量算子解调机械故障诊断方法．振动、测试与诊断，2012，32(6)：915-919．

[9]李学东，张云，马晓莉，等．基于振动分析的滚动轴承故障诊断系统设计．仪表技术与传感器，2012(8)：71-73．