时分双工单源双宿两跳级联网络的容量研究*

管瀚洋，刘锋，曾连荪

(上海海事大学，上海201306)

在船舶通信中，船队会组成链式队列进行航行。船队传递消息可以从一艘船接力传递给下一艘船，每艘船需要准确分离接收自己所需的消息，组成一种多目标链式级联网络。每一艘船既是消息的接收方，又是传递消息的中继方。对于这种单一信源多个信宿所组成的链式级联通信网络的容量、可实现速率等问题，学术界研究较少。本文考虑该实际环境，对其中的单源双宿两跳级联网络进行研究。

无线网络信道容量的问题最早源于参考文献[1]提出的多用户信息理论，虽然没有给出容量表述，但定义了MAC信道；参考文献[2]对MAC信道提出了一种简单的描述；参考文献[3]首次提出广播信道模型；参考文献[4]针对三终端（或节点）模型定义并研究了中继信道；参考文献[5]完善了该理论，虽然结论只针对单源单宿模型，但对于整个网络信息理论具有重要意义。

由于物理限制，实际网络中无线节点无法在全双工模式下进行同时同频收发，只能采取半双工模式。本文将对时分双工模式下单源双宿两跳级联网络的容量区域进行研究和分析。

1 系统模型

考虑图1的单源双宿级联无线网络，定义信源S向目标D1和D2分别传输消息x1和x2，D1接收x1和x2并解码分离出x1后作为中继R并采用解码转发策略将消息x2转发给目标D2，信源S与节点D2不考虑协作。由于系统采用时分双工，节点不能同时接收与发送。若消息x2不为空，则完成一次网络传输需要两个时隙：

时隙1：源S将消息x1和x2发送给目标D1；

时隙2：目标D1作为中继R传输消息x2给目标D2。

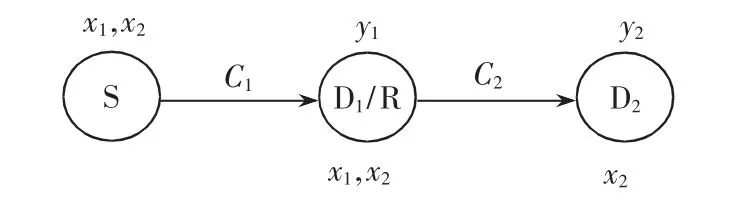
图1 单源双宿级联网络模型

假设完成一次完整的传输所用时间为1，第一跳时隙长度为t，忽略保护间隔，则第二跳时隙长度为1-t。设每个节点都以满功率发送消息，第一跳容量为C1，第二跳容量为C2。

2 单源双宿两跳级联网络容量研究

2.1 网络信息论基础

定理1网络流图中源节点s发送信息到目的节点t，其流量w的最大值等于所有s与t之间割集容量的最小值，即:

[6]采用构造性证明该定理是可实现的。该定理表明源节点与目的节点之间的最大流量等于其中最小的一个割集流量，这就是最大流-最小割定理。

定理2若信息传输速率集合{R(ij)}可达，则存在联合概率密度分布p(x(1),x(2),…,x(N))，使得对于任何S⊂{1,2,…,N}，有：其中边割集τ把网络节点分割成不相交的两个子集S和Sc，Sc是S的补集，如图2所示。

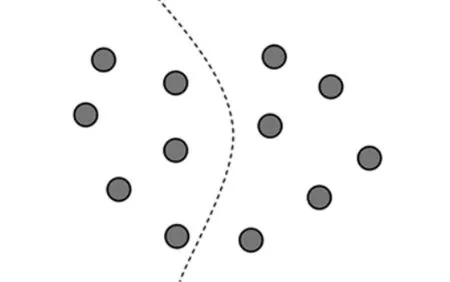
图2 多端网络

定理2的证明可参考文献[4]，主要利用费诺不等式和互信息的性质。参考文献[7]证明了多状态网络容量的割集上界。

图3为广播信道的网络流图，参考文献[8]给出了广播信道容量区的一个简单外界。

图3 广播信道

定理3广播信道的任意可达码率(R1,R2)必存在某个分布q(x)，满足:

这个边界表示的正是当两个译码器合作译码时可达的最大码率。对于广播信道，两个接收机独立工作，所以它的可达码率不会大于合作译码所能达到的码率。

2.2 时分单源双宿两跳级联网络容量区域外界

图1所示的时分单源双宿两跳级联网络由于中间节点同时要担负接收和中继两项工作，常规级联网络模型并不适用于本网络。根据在第一时隙，源节点需要将多个消息同时传输给中间节点，第一跳可以理解为源节点采用广播信道的方式将多个消息发送给中间节点。该模型可以等价为图4的形式。

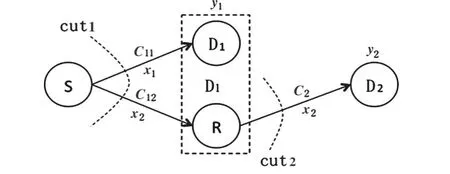
图4 单源双宿级联网络等价形式

时隙1:源S利用广播信道将消息x1和x2分别发送给目标D1和R；

时隙2:目标R作为中继节点传输信息给目标D2。

设D1接收信号为y1，D2接收信号为y2；传输x1和x2的速率分别为R1和R2，总速率R=R1+R2；信道容量分别为C1和C2，其中C1分为C11和C12两部分，C11用于传输x1，C12用于传输x2。

由于采用时分，割集须考虑链路激活时间。根据割集定理，可将单源双宿两跳级联网络分割为：

割集1：

割集2：

综合得单源双宿无线网络的容量区域外界：

定理4单源双宿两跳级联网络的容量区域外界：

证明：

根据式(6)的约束区域，虽然R2的取值取决于其中的最小值，但为了避免通信资源的浪费，两跳链路上传输的关于消息x2的信息量应保持平衡，即tC12=(1-t)C12，有:

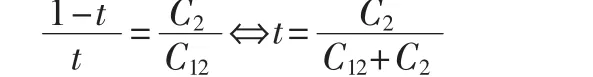
该t值平衡了消息x2的两跳发送，同时包含了两个宿节点各自的信息量权衡，因此它就是最优时间分配系数：最后将topt代入上界约束条件式(6)中即可得出容量区域外界。

2.3 时分单源双宿网络的可实现速率

根据信息论，点对点传输信息的最大可实现速率等于信道容量。参考文献[7]指出了在多终端级联网络下可实现速率：

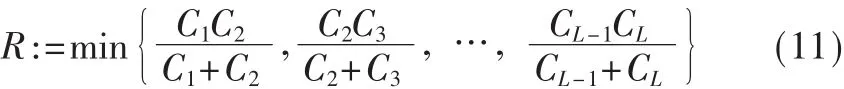
其中{C1,C2,…，CL}是每一跳的可达速率，也就是该信道的容量。对于双跳网络，式(11)可简化为：

下面分别证明R1、R2、R的可实现性：

(1)只传输x1

假设S只传输x1，不传输x2，D1只作为目标存在。C1全部用来传输x1，C11=C1，C12=0。代入(7)可得R1的最大可实现速率为:

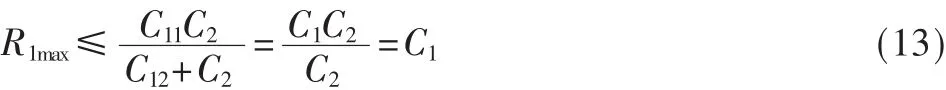
满足点对点传输可达速率的最大值，因此R1完全可以实现。

(2)只传输x2

假设S只传输x2，不传输x1，D1只作为中继R存在。C1全部用来传输x2，C11=0，C12=C1。则代入式(8)得到R2的最大可实现速率：

符合参考文献[8]提出的最大可实现速率，R2的可实现性得证。

(3)同时传输x1和x2

根据式(6)的制约关系，R1和R2虽然无法达到单独传输时所能达到的最大速率，但根据式(7)、式(8)有：

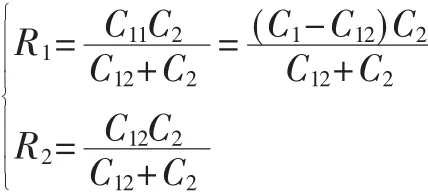
R1和R2都受C12影响。调整C12可以使R1和R2同时满足式(7)、式(8)给出的容量最值，又因为R=R1+R2，因此式(9)推导的总速率R可实现。

3 分析与讨论

将式(10)的时间分配系数t进行等价变形为：

根据式(15)，t的取值范围和变化幅度会随β变化。这里分别取β={0.5，1，2}三组数据进行分析。选取C1=10，C2根据β的选取进行调整,如图5所示。图中t是C12的单调递减函数，减小速率取决于信道容量比β。β越大，t衰减速度越快，t可取值范围越宽；β越小，t衰减速率趋于平缓，t可取值范围相对变窄。

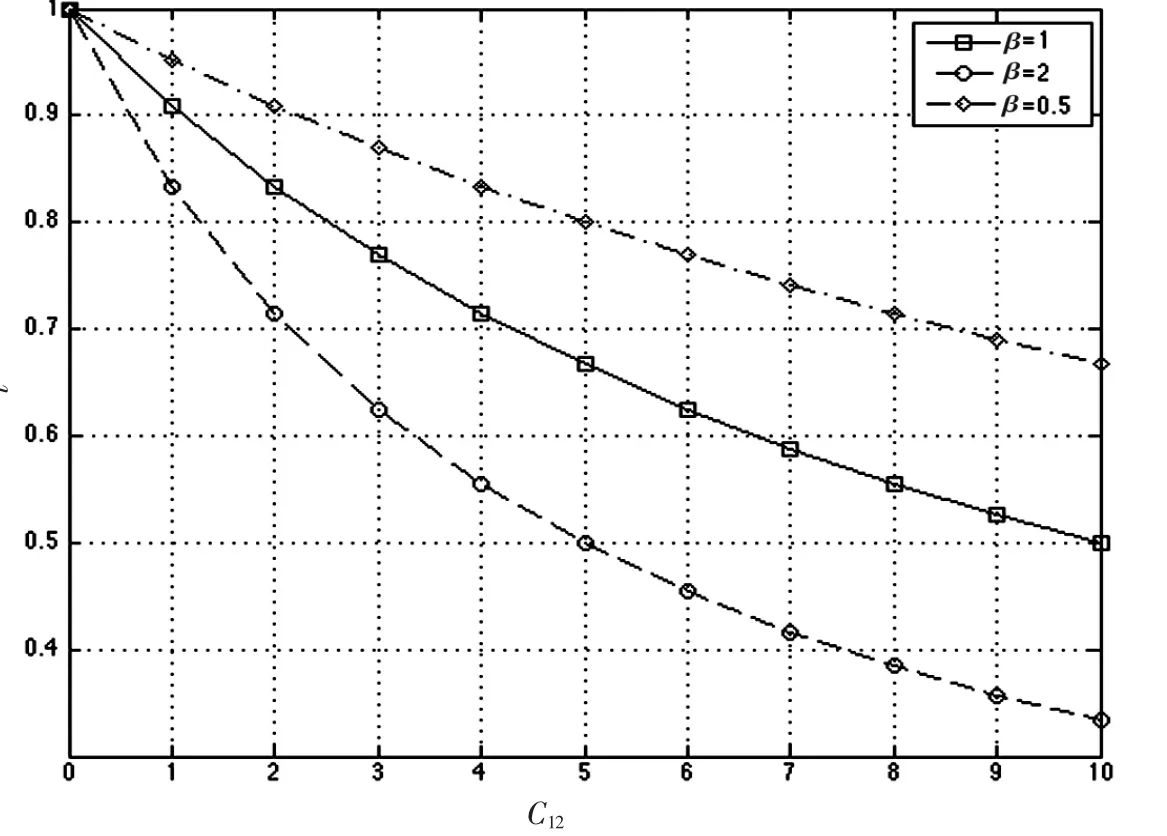
图5 时间匹配系数t的变化趋势

容量曲线同样受β的影响，以β=1为例，选取C1=C2=10，如图6所示。可以看出：(1)R1随C12增加，衰减的速度最快；(2)C12取值最大时息的极限速率R2就是总速率R的最小可达速率，R的最小速率与β的取值成反比关系。

综合图(5)和图(6)有：增大β，消息x1根据C12的调节将占用更短的时隙,代价是牺牲了总体传输速率；减小β，可以提升R的最小传输速率，但会增大第一跳传输消息时所占用的时隙比例。在实际中，需要综合其他因素进行取舍，找到适合当前环境下的参数。

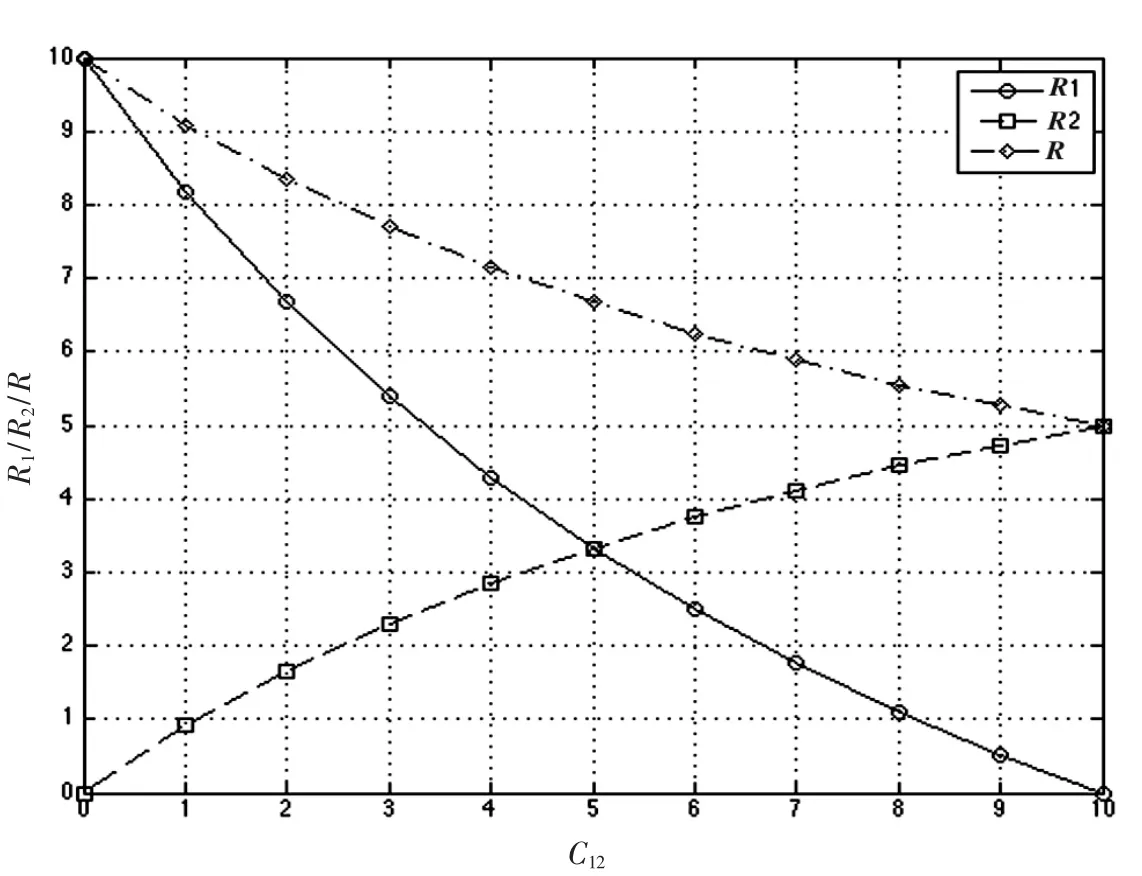
图6 网络各部分容量变化

本篇论文依据最大流-最小割定理研究讨论了时分双工单源双宿两跳级联网络的容量问题。建立了求解处理无线网络容量外界的有效方法，利用该方法找到了该模型的容量区域外界，并对其可实现性进行了证明。最后进行了分析验证，揭示了两个信宿如何有效利用信道资源来完成各自消息的传输问题。

参考文献

[1]SHANNON C E.Two-way communication channels[J].In:Proc.4th Berkelev Svm Math.Statist.and Prob.1961,1(VD):611-644.

[2]AHLSWEDE R.Multi-way communication channels[C].in Proc.2nd Int.Symp.Information Theory.Tsahkadsor,Armenian S.S.R.,1971:23-52.

[3]COVER T M.Broadcast channels[J].IEEE Trans.Inform.Theory,1972,IT-18,Jan:2-14.

[4]COVER T M,THOMAS J A.Elements of information theory[J].Wiley Series in Telecommunications,1991.

[5]SENDONARIS A,ERKIP E,AAZHANG B.User cooperation diversity.Part I system description[J].IEEE Trans.Commun,2003,51(11):1927-1938.

[6]卢开澄,卢华明.图论及其应用[M].北京:清华大学出版社,2005.

[7]KHOJASTEPOUR M A,SABHARWAL A,AAZHANG B.Bounds on achievable rates for general multi-terminal networks with practical constraints[C].Information Processing in Sensor Networks(Lecture Notes in Computer Science).Berlin:Springer,2003.

[8]SATO H.An outer bound to the capacity region of broadcast channels[J].IEEE Trans.Inform.Theory,1978,24(3):374-377.