XCTD剖面仪传输线分布电容对线轴等效电感量的影响

赵　宣，郑　羽，，李　静，王金海，李红志，刘　宁

(1．天津工业大学电子与信息工程学院，天津　300387；2．国家海洋技术中心传感器室，天津　300112)

0　引言

抛弃式盐、温、深(以下简称XCTD )剖面仪探头从船上发射，入水后开始测量。随着测量探头下沉(速度约为3～5 m/s)[1]，探头内部的数据采集器实时完成温度和电导率的采集、处理，并以数字信号形式通过探头内藏的传输线同步上传。XCTD 探头与测量船上数据接收机之间的数据传输系统性能的优劣，将直接关系到温度电导率剖面曲线的真实性，因此，数据传输系统是XCTD剖面仪的重要组成部分。然而由于传输电缆间阻抗参数随放线长度不断变化，影响了XCTD剖面仪信道传输的稳定性，这对信号的完整性造成了破坏[2-3]。XCTD传输线为双股漆包线作为传输导线，线缆的两根导线在海洋中平行排列，该传输线表面覆有绝缘涂层，在上下两个线轴上螺旋紧密缠绕。其平行圆环导线结构如图1所示，内环为传输电缆，半径为 0．05 mm．外环为绝缘漆包半径为0．054 5 mm，周围为海水，信号采用差动传输的方式[3]。

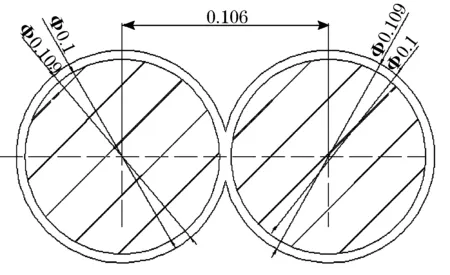
图1　传输线截面模型

1　信道分布电容计算方法及结果

1．1信道线间分布电容的计算

电缆在工作的过程中其周围的工作环境为海水，海水介质为一个弱导体，其存在电容耦合效应，因此电容值就由两根导线间的电容值和导线与海水之间的电容值组成，增加了电容计算的复杂性[4]。随着线缆的展开，分布电容的数值将不断增大，在信道阻抗中将起主导作用，在实际应用过程中，深水信道电容测量难度大，因此利用仿真计算对实际测量具有重要的意义。

文中通过在Comsol中建模仿真，对传输线分布电容进行求解。建立的模型高度1 m，其中，电缆中的绝缘材料选用聚苯乙烯εr=2.6，由于海水介质影响和小的电极尺寸，会增加电容的计算难度和复杂度，因此采用仿真软件Comsol，结合正确偏微分方程，通过场论的计算方法，尝试计算电容值。仿真计算的结果为1 m传输线间分布电容值为2．006×10-10F[5]，测量结果为9．210×10-9F．计算结果与测量值有一定差距，因为由于Comsol软件在计算过程中对于网格划分要求较为细致，文中模型电极面积较小，长度较大，网格划分十分复杂，为了简便计算，文中采用了简单的网格划分方法，导致计算误差较大。该方法还有待改进，今后尝试在更高的硬件平台下验证计算，故文中电容参数选取测量值作为信道模型建立的参考值。

1．2线轴间分布电容的测量

分别在空气介质中，和海水介质中，利用Agilent 4294A阻抗分析仪测量40 Hz～10 kHz的扫频频率的条件下测量了长度为500 m、 600 m的水下线轴和长度为1 100 m、1 300 m的水上线轴。实验结果如表1电容测量值所示。测量海水介质的水下信道电容值在km展开后其数值约为0．2×10-6F，该数值会严重影响传输信号相位的变化。

2　信道螺旋电感和等效电阻测量与计算方法

2．1螺旋电感值的测量方法

由于XCTD剖面仪主要应用于深海海洋环境测量，在工作状态下，实地测量困难很大，目前对XCTD缠绕电感计算主要采用分析了初次级线圈主要几何参数，根据原始电感计算公式计算的方法[6]，这些计算过程相对复杂，限制条件较多，不易快速估算线圈缠绕电感的值，文中考虑到XCTD螺旋线圈紧密的缠绕在圆柱型骨架中，为标准螺旋电感，与ANSYS软件中Brooks Coil Inductance电感计算的原则(如图2所示)，基本应用原则相似，故文中应用该模型计算原理对缠绕电感进行估算。其理论计算公式如式(1)所示：

L=1.699×10-6×R×n2

(1)

式中：L为缠绕电感的数值；R为圆柱型骨架的外径；n为缠绕圈数。

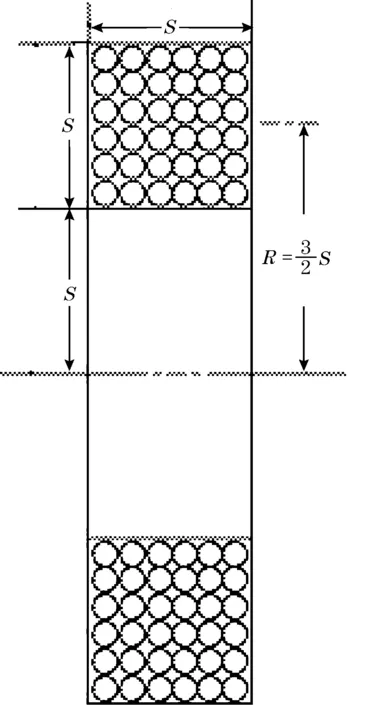
图2　Brooks公式应用模型

利用Agilent 4294A阻抗分析仪在40 Hz～10 kHz的频率的范围内，分别测量线圈长度500 m、 600 m的水下线轴和1 100 m、1 300 m水上线轴传输电缆在空气介质和海水介质中的电感值，测量结果如表1中电感项所示。

对测量结果与计算结果进行比较，可以看出由于Brooks Coil Inductance电感计算的原则规定线圈为规则的正方形且边长与半径相等 ，文中中线圈并不是标准的Brooks相似型，所以导致计算结果和实际测量存在一定的差异。然而，估算结果和实际测量值在同一数量级，且数值误差比在100%～300%左右，虽然Brooks Coil Inductance电感计算的原则规定的计算环境为空气介质，然而，比较海水介质和空气介质的测量值，可以看出，计算结果更加贴近海水中测量的缠绕电感值，基本能满足估算需求。随着线圈模型逐渐逼近相似型，计算与实际的误差比例也逐渐减小，且比值波动也趋于平稳。所以，可以利用Brooks Coil Inductance公式在难以测量的情况下，对线轴缠绕电感进行快速估算。

2．2平行导线电阻的计算

因为信号传输频率在800 Hz左右，频率较低，文中采用导线直流电阻值的计算公式如式(2)对信道分布电阻值进行估算。

(2)

式中：R为平行导线电阻；ρ为工作温度下电阻率；Cj为绞入系数，多股导线为1．02；L为导线长度；A为导线横截面面积。

利用Agilent 4294A阻抗分析仪对不同规格的导线进行电阻测量，部分数据如表1线圈参数实验数据表中所示，推导出单位长度分布电阻值的测量值为2.244 Ω/m．假设材料性质不随环境的变化而改变，根据式(2)计算，得出分布电阻的计算值为2.256 Ω/m，计算值与测量值基本相符。

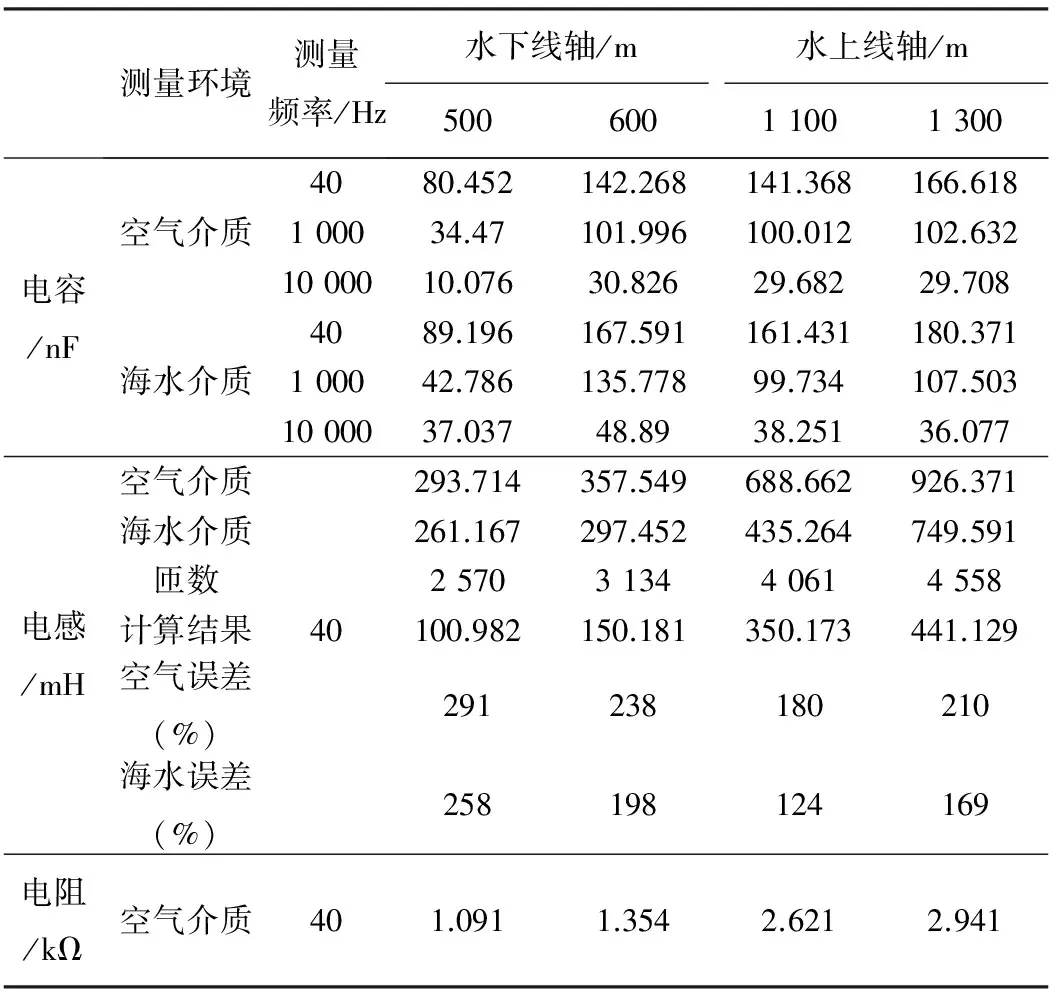
表1　线圈参数实验数据表

3　传输线分布电容对线轴等效电感量的影响

3．1传输信道电路模型

通过上述的测量和计算，得到传输线的螺旋电感的自感量，平行导线间的分布电容、螺线电感上的分布电容以及导线电阻等参数，由与XCTD传输系统传输线对称，为了更好地分析电路间各个电参数之间相互影响作用，得出线轴在传输过程中的简化电路图如图3所示。

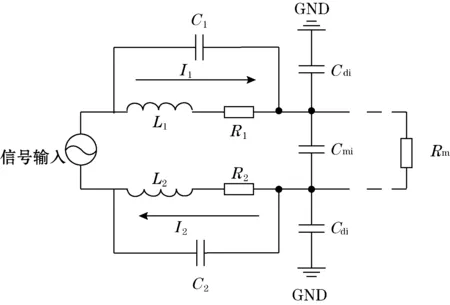
图3　信道分析简化电路图

可以看出，当电容C值小时，对电流基本没影响，由于平行传输线间间距很小，匝数很大，这样基本可以认为I1电流对电感L1形成的磁通量，完全通过L1、L2，因为I2与I1大小和相位相等方向相反，I2在L1上产生互感磁通量与I1在L1上产生的自感磁通量相等方向相反，相互抵消，同理，I1在L2上产生互感磁通量与I2在L2上产生的自感磁通量也相互抵消。因此，理论上，可以认为电感参数对信号基本没有影响。然而，根据文中第二节，传输线在实际测量中km分布电容为μF量级，电容对交流信号相位延时的作用不能忽略，I2并不能严格保证相位不变。

3．2信道传输性能实验

针对第二节问题，文中利用信号发生器发送Vp-p为4．2 V的不同频率的正弦波，通过输出端并联0．1 nF、1 nF、10 nF、和100 nF的瓷片电容，观察水下500 m传输线轴的信号输出特性。其中500 m标准水下传输线自身电感293．714 mH，分布电容为80．452 nF，分布电阻1．08 kΩ．通过该实验系统，对得出的数据进行处理，得出不同分布电容下的信道频带特性如图4所示。

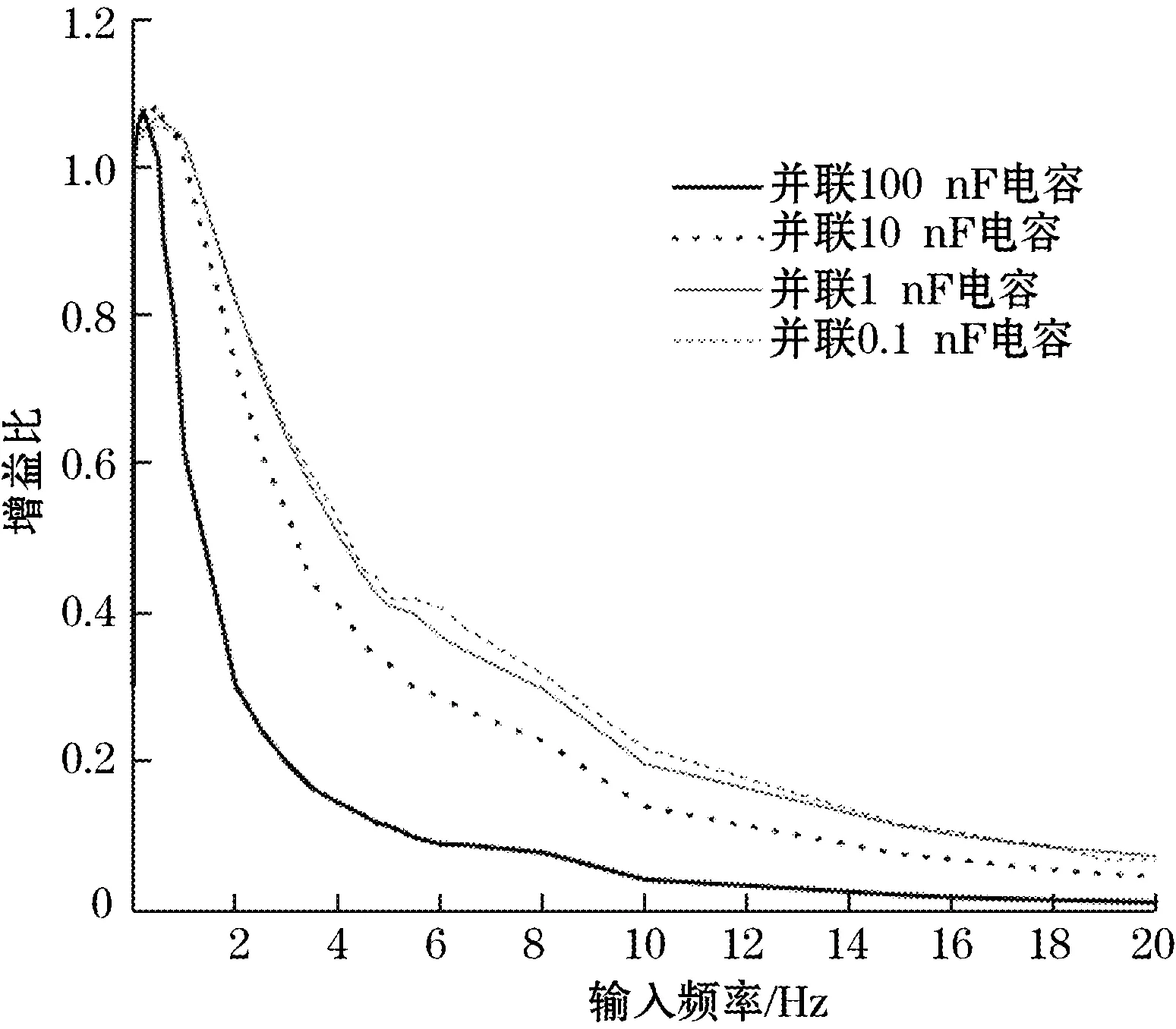
图4　信道频带特性实验分析图

图4可见，传输线呈现的是带通滤波特性，最大增益为1．1左右，通频带100～1 000 Hz，在随着并联电容值的不断增加截止频率不断减小，高频衰减加快。因为500 m水下传输线轴自身并联电容为80 nF，所以并联较小的电容对传输特性影响不大，然而随着并联电容逐渐增大，发现相位偏移的频率值逐渐变小，随着频率的增大，相位偏移也逐渐增大，增益减小，通频带变窄。

3．3分布电容对等效电感量影响的分析

根据图3的信道简化电路图模型。推导信道传输函数。由于线间分布电容值为80 nF，数值较大，自身分布电容Ci和对地电容Cdi的影响基本可以忽略，负载端为1 MΩ的采样电阻Rm，输入信号的方程公式如式(6)所示：

y=cos(2πf0t)u(t)=cos(ω0t)u(t)

(6)

设L为L1和L2的和，R为R1和R2的和，则函数的传递方程如式(7)所示：

(7)

根据式(7)所得的简化电路传递方程，对500 m标准水下传输线的传输信道用Matlab进行幅频特性和相频特性分析，分别使分布电容值C的值为线圈分布电容与104的电容并联后的总值180 nF和单一线圈分布电容80 nF，与图4中并联104电容的实验曲线和无并联电容的试验曲线进行对比，分析电路实际螺旋电感量，结果如图5、图6所示。

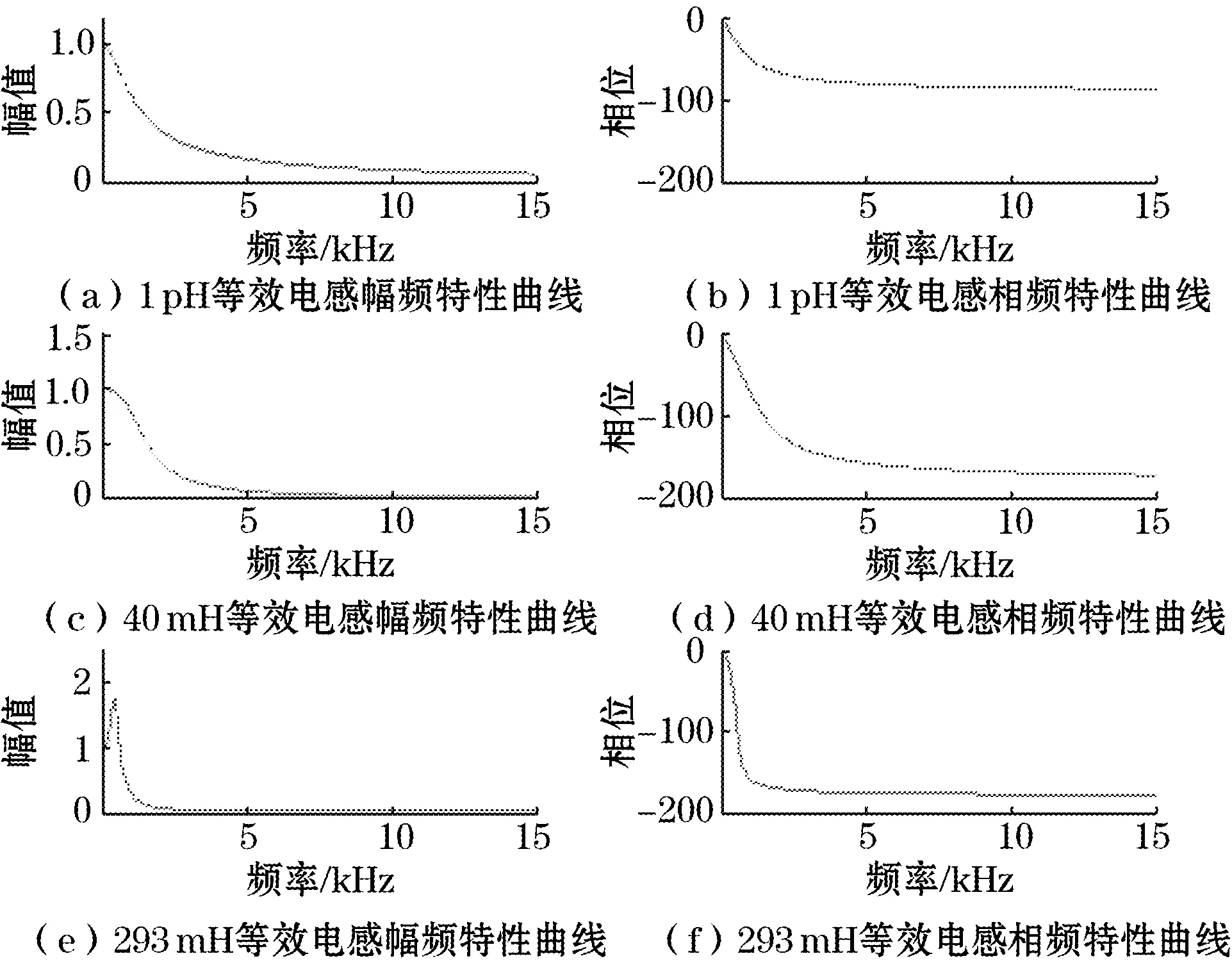
图5　180 nF分布电容对螺旋电感的影响

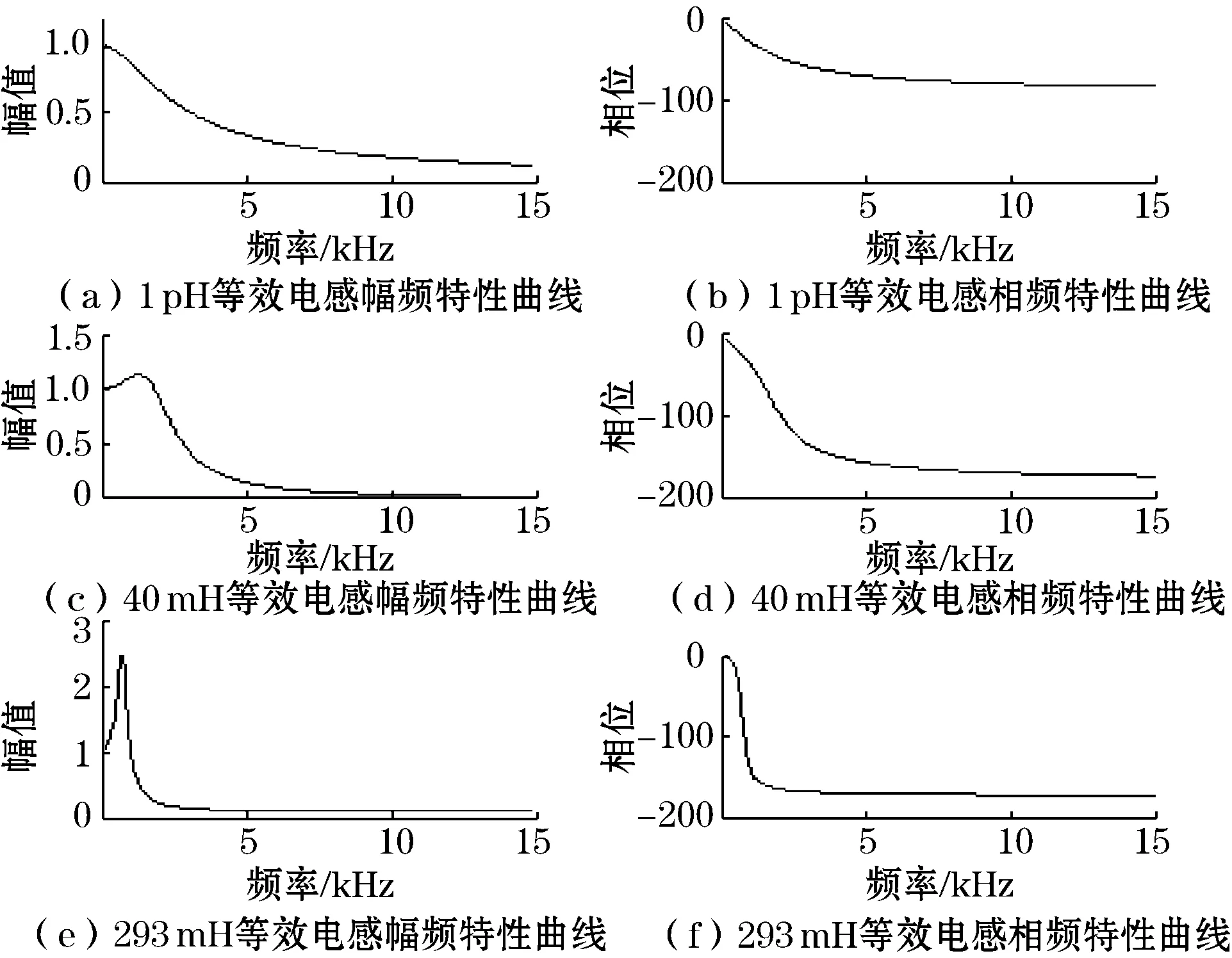
图6　80 nF螺旋电感对信道传输函数的影响)

当分布电容为180 nF，自感与互感抵消的情况下，等效电感值L为1 pH，电路传输函数幅频特性呈现出低通特性与之前的实验数据统计的带通特性不相符，相位衰减小于100°；不考虑自感互感抵消作用的影响，电路等效电感值L为测量值293 mH，传输线输出最大增益的频率在700～800 Hz，最大增益时，相位衰减约为30°，增益达到1．5以上，也不完全附和之前实验的结果，考虑部分自感互感抵消状态的影响，在电路实际等效电感L均为50 mH的情况下，增益约为1．1左右，通频带在100～1 kHz左右，与之前的实验结果类似。同理，分布电容值减至80 nF，在电路实际等效电感L均为40 mH的情况下，才能使传输函数幅频特性与测量特性相符。

可以看出线传输中分布电容的存在，不但对信号产生衰减作用，还会引起的电流相位失真，从而影响接入电路中的等效电感的值，比较图5，图6中的结果，可以看出这种影响，随着等效分布电容的减小而逐渐减小的。在分布电容一定的情况下，对比3种不同的接入电感的幅频、相频特性图，可以看出，缠绕电感越大，信号最大增益越大，电流的相位平移越严重。幅频特性曲线变化速率越快。

4　结束语

文中针对XCTD 剖面仪的信道特征，采取试验测量，软件仿真以及理论计算等方式相结合的研究方式，讨论了软件仿真计算XCTD剖面仪分布电容的可行性，提出了估算线圈缠绕电感值和分布电阻的方法，从而得到系统的阻抗参数，进一步得到了信道简化电路模型，并在此基础上讨论了分布电容对等效电感的影响，实验表明，当接入电路中的电感量不变，信道的通频带随分布电容的增大而变窄。当分布电容一定，缠绕电感越大，信号最大增益越大，电流的相位衰减越快。幅频特性曲线变化速率越快。同时，平行长距离有线传输过程中，分布电容的存在，不但产生衰减信号的作用，还增大了缠绕电感接入信道的等效电感，从而进一步影响信号稳定传输。在此基础上，量化各阻抗参数之间的影响关系，对信道环境进行优化和平衡，成为下一步研究的重点问题。

参考文献：

[1]孙涛，黄银水，陶建华．抛弃式温盐探头运动的数值模拟及其实验验证，海洋通报，2002，4(4)：69- 76．

[2]范寒柏，彭安，王少仙．抛弃式海水电导率测量电路设计．仪表技术与传感器，2010(11)：91-95．

[3]邵毅，李建国，王欣，等．6000m电缆传输CTD剖面仪数据采集系统设计．海洋技术，2010，29(4)：4-8．

[4]刘沁，周东旭，张治国，等，电容式压力传感器的线性化校正与温度补偿．仪表技术与传感器，2010(11)：1-3．

[5]郑羽，李红志，梁捷，等．水下XCTD剖面仪传输线间分布电容的建模与计算．海洋通报，2013(3)：24-28．

[6]刘修泉，曾昭瑞，黄平，等．空心线圈电感的计算与实验分析．工程设计学报，2008，15(2)：149-153．