多声道超声流量计的延时补偿及定时误差

刘艳萍，王献勇，赵连环

(1．河北工业大学信息工程学院，天津　300401；2．唐山世佳电子有限公司3，河北唐山　063000)

0　引言

多声道超声流量计具有计量精度高、对管径的适应性强、无压力损失等优点，多声道布置方式改善了单声道布置在非理想流场下测量精度相对较低的缺点，提升了计量精度，并且增强了对流速波动的抗干扰能力[1]。可用于大管径测量，解决了流体流速分布对测量精度的影响，具有较高精度[2]。

通过多声道超声流量计不同的弦向声道长度，在静水状态下，可以计算出硬件电路和超声换能器以及算法原理上的平均延时，用以补偿测量的平均传输时间，提高时间测量精度。在常态测量状态下，计算各个弦向声道的定时误差，判断其是否出现跳峰等错误，而进一步修正测量时间。

1　超声波测量原理

时差法原理[3]如图1所示，流体的速度为v，超声波在静止流体中的速度为c，管径为D，发射角度为θ，tU、tD为正逆程传播时间。

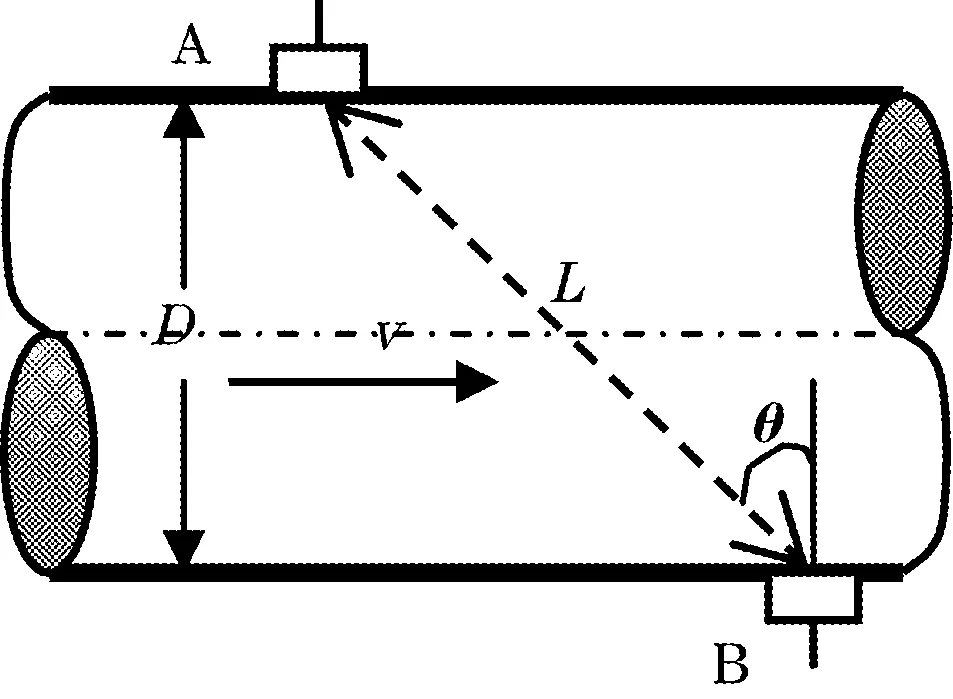
图1　速度差法原理图

顺流时超声波在流体中的传播速度为：

(1)

逆流时超声波在流体中的传播速度

(2)

两式相减，并考虑到Δt=tD-tU，可以得到

(3)

2　多声道流量计的原理

2．1四声道流量计的声道分布

多声道超声波换能器分布在测量管段的不同流层，大多数采用偶数声道的布置方式，可以更好地反映流体流速分布的对称性。有多种多声道超声流量计的声道布置方式，包括平行方式、对角方式和网络方式等[4]。文中采用四声道平行声道布置方式的多声道超声流量计，分布方式如图2所示。

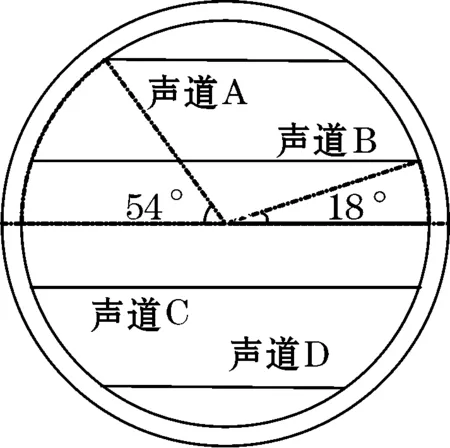
(a)

(b)

其中，超声波换能器安装方法采用直插法[5-6]，入射角度为45°。4个声道A、B、C、D的安装角度分别为18°和54°．管道外径为216 mm，壁厚8 mm．

2．2多声道流量计的流速计算

该四声道超声流量计采用时差法的测量原理[7]。根据时差法的工作原理，从管道的横向方向看，在各个声道分布的弦线上，如图2(a)，第i个弦向声道沿轴线方向的平均流速为

(4)

式中：vi(ri)为第i个弦向声道沿轴线方向的平均流速；Li(ri)第i个弦向声道的声程；θ为弦向声道与轴向方向的夹角，即入射角度；tUi为第i个弦向声道超声波正程传播时间；Δti为第i个弦向声道正逆程传播时间差。

根据4个不同弦向声道所测得的平均流速，采用加权的方法，得到多声道超声流量计流过横截面的平均流速(即瞬时流速)为

(5)

式中：Wi为第i个弦向声道的加权系数。

在文中的声道分布方式中，N=4，加权系数分别为0.228 75、0.257 5、0.257 5、0.228 75。

3　时差法的测量延时与补偿

3．1测量延时

四声道超声流量计采用时差法的测量原理，当某一程开始，系统发出一束方波信号，通常是差分信号，来激励超声波换能器，使电信号转换为超声波信号发送出去。超声波信号通过一段长度的声程，到达接收端的超声波换能器，换能器将超声信号转换为电信号，送往采样电路，通过相应的算法确定超声波的到达时刻[8]。正逆程时间测量原理如图3所示。

图3　时间测量原理

图3中：A为系统发出激励信号的起始时刻；B为超声波从换能器翻出的时刻；C为超声波到达接收换能器的时刻；D为测量算法确定的到达时间；τ1为声波在声楔和电路中传输时间，称为电路延时；t为超声波在声道中的实际传播时间；τ2为测量算法确定的到达时刻与实际到达时刻的差，称为声道延时；T为测量得到的总的超声波传播时间。

采用的到达时刻确定算法为阈值法，即当接收到的超声波信号幅度超过某一设定预知的时候，将该波的下一个过零点作为超声波的到达时刻。一般来说，声波在声楔和电路中都会有一定的传输时间，即为电路延时。同时，测量算法确定的到达时刻与实际到达时刻之间会有一定的差值，即为声道延时。如图所示，由于有电路延时和声道延时的存在，使得根据算法测得的总的超声波传播时间总是大于超声波实际的传播时间，即

T=t+τ1+τ2

(6)

3．2测量延时补偿方法[9]

四声道超声流量计拥有2个不同的声程长度，LA和LB分别为声道A和声道B的声程。假设，在2个不同声程长度的弦向声道中，超声波在流体中的声速c和延时τ相同，其中τ=τ1+τ2。在静水状态测量时，测量得到的超声波总的传输时间为T，则

(7)

由式(7)可以得出延时τ为：

(8)

在实际操作过程中，可以通过式(8)来确定延时τ，单通常情况下τA≠τB。习惯的做法是在生产制造的过程中确定超声波换能器和电路的延时时间。知道了延时τ，就可以用来校正传输时间，测量得到的超声波总的传输时间T中减去延时τ就得到了超声波在声道中的实际传播时间t。

3．3定时误差

(9)

定义一个新的变量η，则

(10)

式中：tm=t+te为减去延时的测量传播时间；te为定时误差。

若所有的时间测量无误，则η=0。若峰值选择错误，出现跳峰的情况，使过零点的确定出现差错，则会产生定时误差te，如图4所示。

图4　过零点选择

若过零点选择错误，定时误差te存在，则

(11)

η的值取决于定时误差te，这是一个很好的估测定时误差影响的方法。四声道超声流量计可以计算出各个弦向声道的定时误差，从而进一步校正测量时间，提高测量精度[10]。

若出现单个跳峰，则η≠0。在文中所用的实验管道中，管道外径为216 mm，壁厚8 mm，LA=166.250 mm、LB=268.999 mm，超声波信号频率为1 MHz ，周期为1 μs，平均流速大约为8 m/s，流体声速为1 482 m/s，测得的η如表1和表2所示，单位为μs．

通过弦向声道A时间测量和弦向声道B时间测量，在测量过程中，若某一声道出现跳峰另一声道正常，或者同时出现跳峰，同时测量正常，则在上述情况下可能的组合如表1所示。

表1　η函数值

4　实验结果及结论

四声道超声流量计的安装方式如图3所示，文中所使用超声波信号频率为1 MHz，流体声速为1 482 m/s．

在静水测量状态下，通过多声道超声流量计不同的弦向声道长度及其平均传播时间，计算得到的电路延时和声道延时之和的平均值，如表2所示。

表2　延时平均值

用表2得到的延时的平均值来补偿超声波在声道中的平均传播时间，在延时补偿前后，测得的超声波在静水中的传播速度如表3所示。

表3　延时补偿前后流体声速　m/s

5　结束语

通过实验结果比较可知，延时补偿可以减少电路延时和声道延时对测量结果造成的误差，提高多声道流量计的测量精度。同时可以在测量的过程中，动态的监测各个弦向声道的定时误差，判断是否出现跳峰等错误，以进一步提高测量精度。

参考文献：

[1]蔡武昌，孙淮清，纪纲，等．流量测量方法和仪表的选用．北京：化工工业出版社，2001．

[2]刘欣荣．流量计，第2版．北京：水利电力出版社，1990：1-5．

[3]李广峰，刘防，高勇．时差法超声波流量计的研究．电测与仪表，2000，37(9)：13-17．

[4]王华青．气体超声流量计测量原理，标定及维护．计量技术，2006(1)：61-2．

[5]李夏青，左丽．超声波流量计换能器的入射角及振荡频率对测量精度的影响．仪表技术与传感器，2000(4)：28-9．

[6]CARLANDER Carl，DELSING Jerker．Installation effects on an ultrasonic flow meter with implications for self diagnostics．Flow Measurement and Instrumentation，2000，11(2)：109-122．

[7]李跃忠，李昌禧．多声道超声气体流量计的建模与仿真，华中科技大学学报，自然科学版，2006，34(4)：39-4l．

[8]张世荣．热式气体质量流量测量及补偿算法研究：[学位论文]．武汉：华中科技大学，2007．

[9]MANDARD E，KOUAME D，BATTAULT R，et al．Transit time Ultrasonic flowmeter：velocity profile estimation．Ultrasonic Symposium，2005，2(18-21)：763-766．

[10]BUONANNO G．On field characteristerisation of static domestic gas flowmeters．Measurement，2000，27：277-285．