基于S变换的复合材料超声回波信号降噪

王振生，王峰林，王长龙

(军械技术研究所，河北石家庄　050003)

0　引言

复合材料由于具有低热胀系数、高耐热性，在动力结构方面的高比强度、高比模量、耐磨损和抗老化等特点，被广泛的应用到固体火箭发动机等生产中[1]。复合材料在生产和使用过程中，不可避免地会产生各种缺陷，严重影响结构的强度，甚至导致事故的发生。超声是复合材料常用的无损检测方法[2]。但由于超声检测复合材料过程中会产生晶粒噪声和电噪声[3]，因此必须对超声回波信号进行消噪处理。

超声信号降噪处理的方法有很多，常用的时频分析消噪方法有短时傅里叶变换、小波变换等[4]。短时傅里叶变换虽然一定程度上克服了标准傅里叶变换不具有的局部分析能力的缺陷，但由于窗函数选定后只能改变窗口在相平面上的位置，不能改变窗口的形状，因此不适用于超声等非平稳信号。小波分析能够对超声信号进行降噪，但小波阈值的选取和小波阈值函数的确定比较复杂，且小波软阈值降噪后信号会产生较大的失真，硬阈值降噪后信号不连续，重构信号会产生振荡[5]。

作为短时傅里叶变换和小波变换的一种扩展，S变换逐渐引起人们的兴趣，S变换(S Transform，ST)是由Stock well等学者于首次提出的[6]，并已在医学信号处理、地震信号处理以及电力技术等领域得到广泛的应用[7-8]。它首先采用具有多种分辨率的与频率有关的可变高斯函数，克服了短时傅里叶变换固定分辨率的不足，同时S变换中含有相位因子，而小波变换则不具备这一特性。而且由于是一种线性时频表示，因此不存在Cohen类分布的交叉项的干扰[9]。变换应用于超声检测回波信号的时频分析还未有报道。因此，文中将变换应用于超声检测信号降噪。

1　超声检测回波模型

超声检测回波信号的数学模型一般可表示为[10]

x(t)=βe-b(t-τ)2cos[2πfc(t-τ)+Φ]

(1)

式中：β为缺陷的反射系数；b为换能器的带宽；fc为换能器的中心频率；τ为缺陷反射回波到达的时间延时；Φ为初始相位。

不同参数对信号误差影响如图1所示。

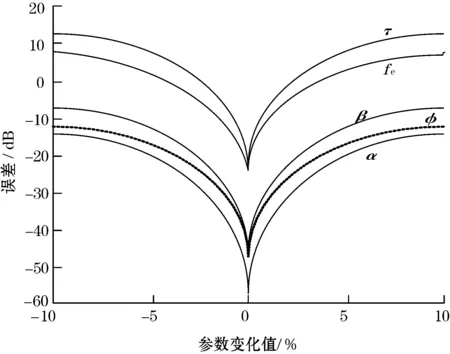
图1　不同参数对信号误差的影响

2　S变换

2．1S变换基本原理

S变换是一种可逆的时频分析方法，是短时傅里叶变换和连续小波变换的一种结合与延伸。通常离散变换可以通过快速傅里叶变换实现：

设离散时间信号为h[kT]，其中k=0，1，2，…，N-1，T为采样时间间隔，N为总采样点数。信号h[kT]的离散傅里叶变换为

(2)

式中n=0，1，2，…，N-1。

离散信号h[k]的S变换离散表示形式为

(3)

S逆变换的离散表达式为

(4)

h[k]变S换后结果为一个二维复时频矩阵，记为S矩阵，其行对应频率，列对应采样时刻。将S矩阵中各元素求模后的矩阵记为S模矩阵，其行向量表示某一频率下信号随采样时刻变化的分布，列向量表示某一采样时刻下信号随频率变化的分布。S模矩阵中各元素反映了信号在其对应时刻及频率下的时频特征，S变换的结果可通过时频图像来直观的表示。

2．2S变换时频滤波过程

S变换的滤波过程可表示为

y(n)=S-1{S[h(n)]H(n，k)}

(5)

式中：S和S-1分别为变换和反变换；H(n，k)为时频滤波因子。

时频滤波因子一般根据信号的瞬时频率被设计成1个二维的窗函数，即

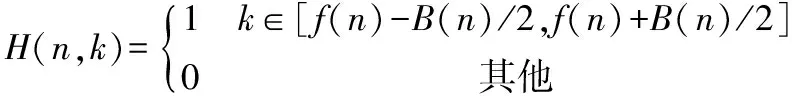
(6)

式中：f(n)为信号的瞬时频率；B(n)为时频滤波器的带宽。

带宽B(n)一般根据信号的能量在时频平面上沿瞬时频率聚集程度来确定。其具体步骤如下：

(1)利用S变换进行频谱分析，估计有效信号和干扰信号的瞬时频率分布特征；

(2)根据时间剖面确定噪声的分布时间及噪声在整个时间剖面上的分布范围，再根据噪声频率的分布特征，确定滤波器的时频滤波因子H(n，k)；

(3)利用S变换计算信号的时频分布S(n，k)；

(4)对S(n，k)、H(n，k)进行反变换得到y(n)，y(n)即为S变换时频滤波的输出。

3　仿真实验与分析

理想超声检测回波信号波形如图2所示，图3为加入服从N(0，0.16)分布的高斯白噪声信号。

经过S变换后的时频分析如图4所示。基于S变换去噪方法是将S矩阵中大于某阈值频率的所有行向量元素取零，而后经S逆变换，得到降噪后的信号。这种算法的降噪效果与阈值频率的选取密切相关。由于超声检测回波信号与噪声的非高斯性不同，经S变换后二者在S模矩阵行向量中的分布必然存在着差异。文中通过求S模矩阵中行向量的非高斯分布，确定主要由噪声经S变换产生的行向量，而后将S矩阵中主要由噪声经S变换产生的行向量的所有元素取零得到滤波算子H(n，k)，再经S逆变换得到降噪后的信号如图5(a)所示，传统小波软阈值去噪方法如图5(b)所示。

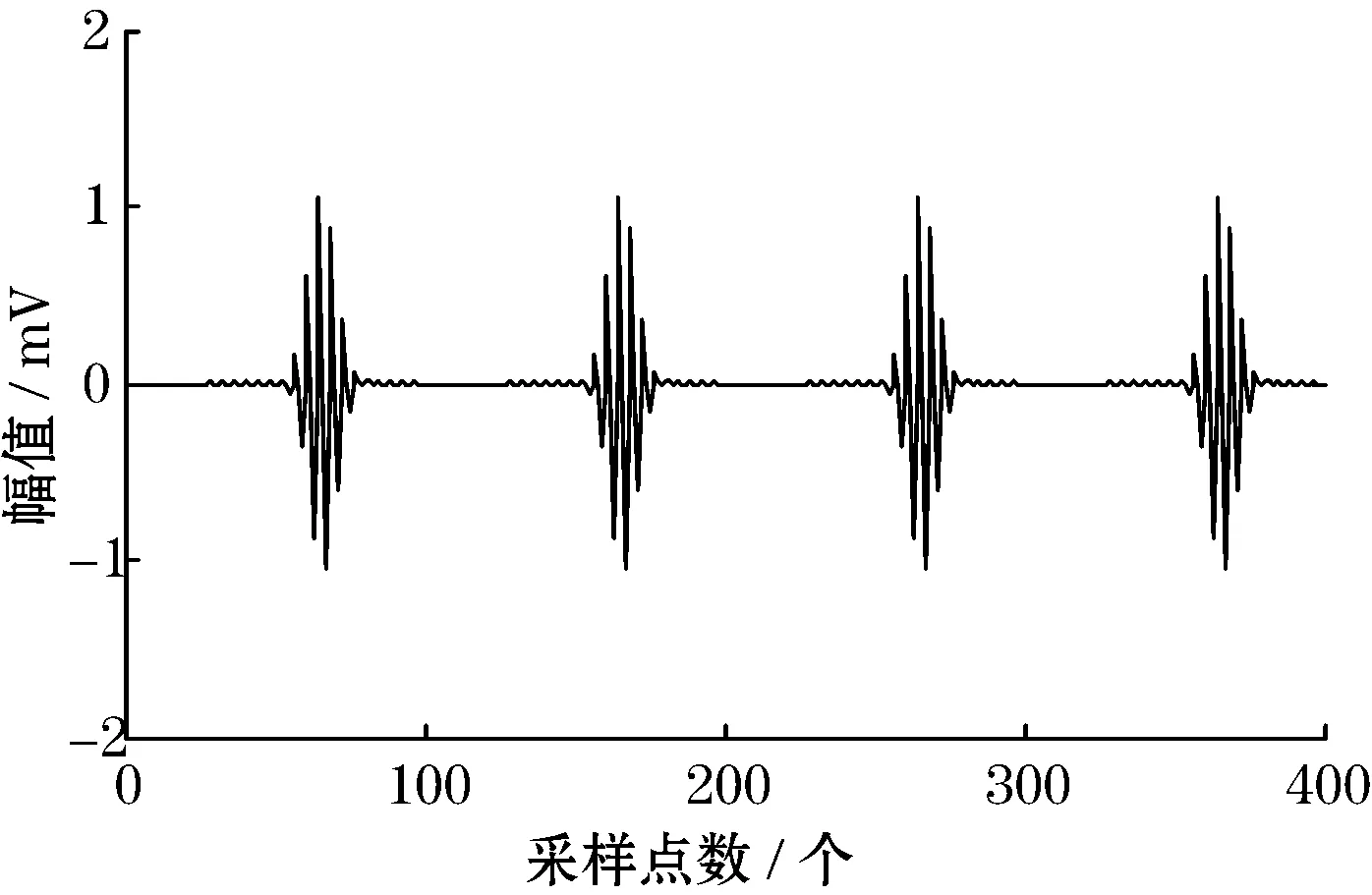
图2　超声检测信号

图3　加噪后的超声检测信号

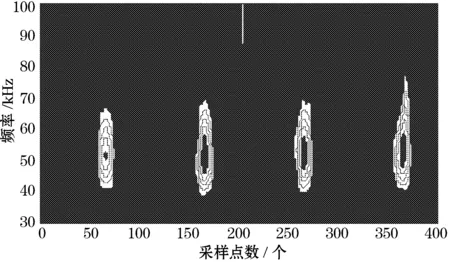
图4　超声检测信号的时频分布

(a)S变换去噪后的信号

(b)小波软阈值去噪后的信号

为了更好地分析检测信号经不同方法降噪后的性能差异，文中用均方根误差(RMSE)和信噪比(SNR)参数进行评估。

均方值误差：

(7)

信噪比：

(8)

式中：xi为原始信号；xi为降噪后的信号；N为采样长度。

由表1可知，基于S变换的方法降低了均方根误差，提高了信噪比。能够较好地对超声信号实现降噪。

表1　两种方法降噪评价指标比较

4　实验分析

实验采用军械工程学院无损检测研究所研制的基于Polar 9300E的超声信号检测实验平台，以某铝金属基复合材料为检测对象。信号发射脉宽50 μs，探头发射频率为5 MHz，声速9 090 m/s，采样频率为50 MHz．采样点数为2 048，取前1 500个。实验采集的脱粘信号如图6所示，图7为新方法去噪后的信号。

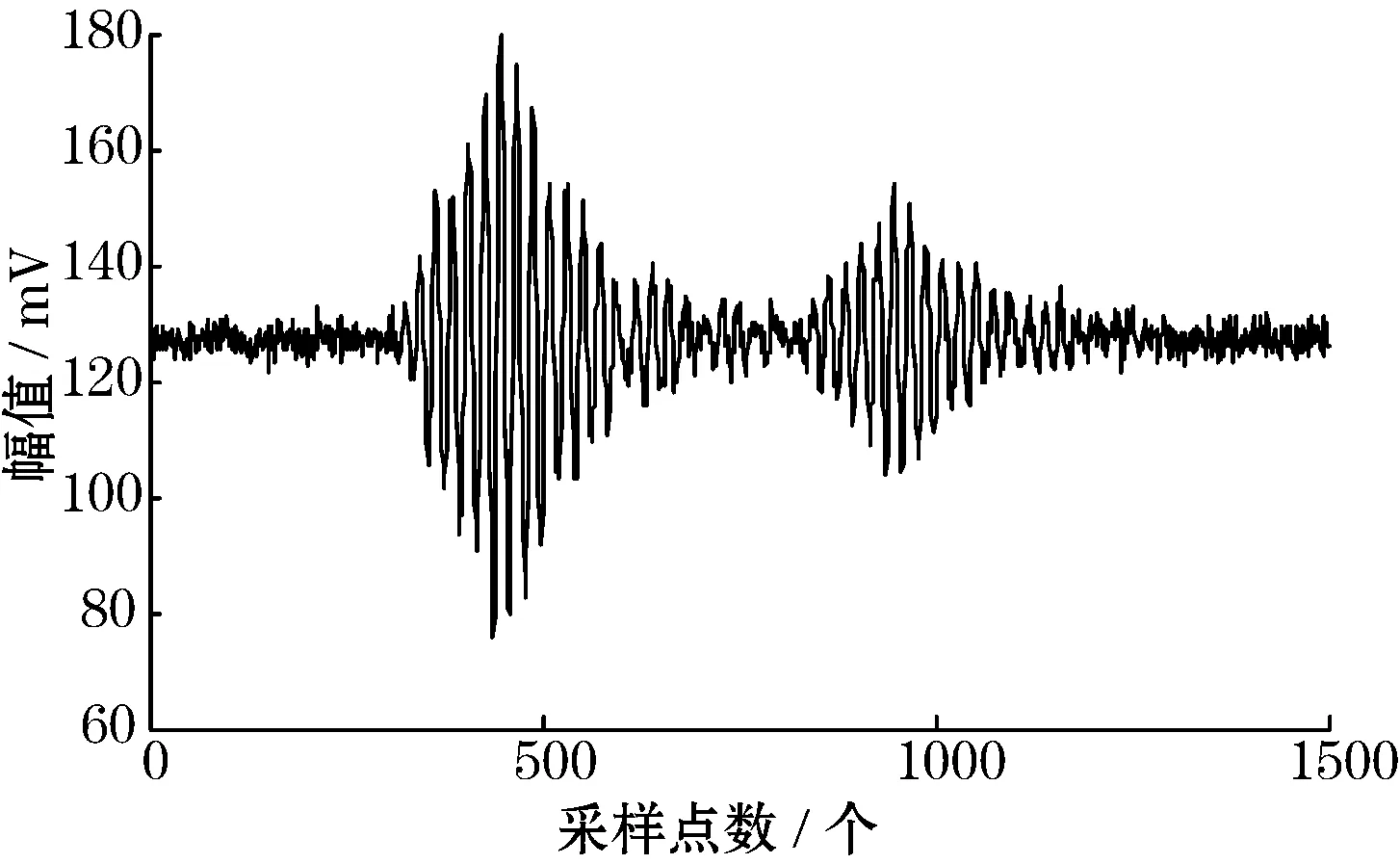
图6　实验采集信号

5　结论

(1)超声检测回波信号中参数因子τ、fc对重构误差影响较大，在超声重构信号时需考虑；

(2)通过分析噪声信号和超声检测回波信号的不同非高斯性，提出基于S变换的超声信号去噪方法；

图7　文中方法去噪后的信号

(3)基于S变换的去噪方法与传统的小波阈值降噪相比进一步降低了均方根误差，提高了信噪比，是一种较好的超声信号处理方法。

参考文献：

[1]RAJMOHAN，PALANIKUMAR K，KATHIRVEL M.Optimization of machining parameters in drilling hybrid aluminum metal matrix composites．Trans．Nonferrous Met．Soc．China，2012,22：1286- 1297．

[2]颜丙生，吴斌，李佳锐，等．金属材料力学性能退化非线性超声检测实验系统优化．仪表技术与传感器，2011(2)：95-98．

[3]周知进，文泽军，卜英勇．小波降噪在超声回波信号处理中的应用．仪器仪表学报，2009，30(2)：237-240．

[4]易吉良，彭建春，罗安，等．电能质量信号的改进S变换降噪方法．仪器仪表学报．2010，31(1)：33-37．

[5]刘守山，杨辰龙，李凌，等．基于自适应小波阈值的超声信号消噪．浙江大学学报，2007，41(9)：1558-1560．

[6]STOCKWELL R G，MANSINA L，LOWE R P．Localization of the complex spectrum：the S transform．IEEE Trans on Signal Process，1996，44(4)：998-1001．

[7]郭灿新，勇明，徐敏骅，等．S变换在电力电缆局部放电信号时频分析中的应用．电工技术学报，2010，25(11)：9-14．

[8]王殿伟，李言俊，张科．基于S变换的时频特征提取与目标识别．航空学报，2009，30(2)：305-309．

[9]李雪英，侯相辉．基于广义S变换的叠前高频噪声压制．石油地球物理勘探，2011，46(4)：545-549．

[10]严寒冰，殷国富．基于MMW和ICER加权匹配的超声缺陷识别．数据采集与处理，2008，23(6)：724-728．