一种参数曲线间Hausdorff距离的计算方法
林 意,薛思骐,郭婷婷
(江南大学数字媒体学院,江苏 无锡 214122)
Hausdorff距离在几何设计、图像匹配、图像识别中有广泛应用[1-2],但是现阶段关于参数曲线间Hausdorff距离[3]的研究较少,计算仍有一定难度,无法通过其定义直接计算获得。Scharf等[4-5]提出了在自由曲线上可能产生Hausdorff距离的4种情况:产生在端点处、极值点处、共线法向点处或是平分线交点处,并给出了对应的求解方程或方程组[6-7]。虽然通过方程组计算Hausdorff距离产生的结果比较精确,但是对于参数曲线来说,求解方程组的复杂度很高,计算较为困难。因此,Chen等[8-10]从几何角度提出了曲线间Hausdorff距离的计算方法,通过不断减小半径的圆弧来排除无效曲线段,直至最后收敛于一个确定的值。这种方法需要计算距离方差,虽然计算量比前种方法小,但仍然不是很方便。此外,在进行圆弧剪枝时,如何判断曲线段是否在圆弧外也较困难。白彦冰[11]将曲线在给定误差下离散成折线,然后在Scharf[12]提出的基于Voronoi图性质的单向Hausdorff距离计算方法的基础上计算折线间的Hausdorff距离,以近似获得曲线间的Hausdorff距离。这种方法无需计算方程,但Voronoi图的构建比较复杂,且在进行曲线离散时采用递归分割的方法,需另外采取节点插入算法,比较繁琐。
本文将曲线绘制过程中产生的折线作为曲线离散折线,然后将曲线间的Hausdorff距离转化为折线间的Hausdorff距离并进一步转化为点到线段间的距离进行计算,并加以必要的剪枝策略[13]以提高计算效率。
1 Hausdorff距离的定义
Hausdorff距离是描述两组点集之间相似程度的一种量度,它是两个点集之间距离的一种定义形式,它具有方向性。假设有两个点集A和B,a和b分别为A和B中任意一点,则点集A到B的单向Hausdorff距离指点集A中每个点到点集B的最小距离中的最大距离,可以表示为:
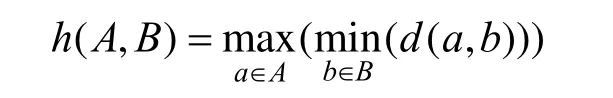
同理,可以表示出点集B到点集A的单向Hausdorff距离h(B,A)。则点集A与点集B之间的Hausdorff距离定义为:
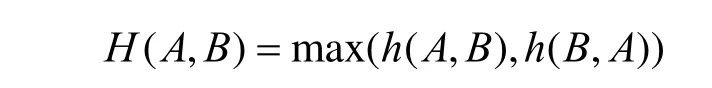
2 参数曲线间Hausdorff距离的计算与优化
2.1 曲线离散
在计算机进行曲线绘制时,通常采用下面算法分段绘制:


也就是说,以折线来近似代替原曲线,而且,折线可以按变量e的改变,很好的逼近曲线,现在,微软的画图软件、AutoCAD等公司均采用这种方法画曲线。
根据这一思想,本文将曲线绘制过程中产生的折线作为曲线离散折线,然后将曲线间的Hausdorff距离转化为折线间的Hausdorff距离并进一步转化为点到线段间的距离进行计算,并加以必要的剪枝策略以提高计算效率。
当然,会不会折线近似代替曲线后的Hausdorff距离误差依旧很大呢?
假设两条曲线分别为r1,r2,相应的离散后的折线为d1,d2,r1与d1的最大误差为ε1,r2与d2的最大误差为ε2。即|r1-d1|≤ε1,|r2-d2|≤ε2。用H(r,d)=|r-d|表示r与d之间的Hausdorff距离,由此可得:

因此,H(r1,r2) -H(d1,d2)≤ε1+ε2
可见,曲线间的Hausdorff距离与离散折线间的Hausdorff距离的误差具有可控性。由于d1越逼近r1,则ε1越小;同理,d2越逼近r2,则ε2越小。进一步就是,d1与d2的Hausdorff距离越接近r1与r2的Hausdorff距离。所以,曲线间的Hausdorff距离可以近似用离散折线的Hausdorff距离来计算。
2.2 折线间的Hausdorff距离计算
折线d1和d2间的Hausdorff距离可以通过计算两次折线到折线的单向Hausdorff距离来获得。计算d1到d2的单向Hausdorff距离时,可以分别计算d1上所有线段到d2的单向Hausdorff距离,然后取其中的最大者作为d1到d2的单向Hausdorff距离。因为d2也是线段的集合,因此根据Hausdorff距离的定义,在计算d1线段到d2的Hausdorff距离时,可以分别计算线段到d2上所有线段的最小距离,然后取其中的最大者作为线段到d2的单向Hausdorff距离。这就将计算折线到折线的单向Hausdorff距离转化为了计算线段到线段的单向最小距离。那么d1到d2的单向Hausdorff距离可以写成如下形式:

我们知道,线段s1到线段s2的最小距离只会产生在s1的某个端点处。
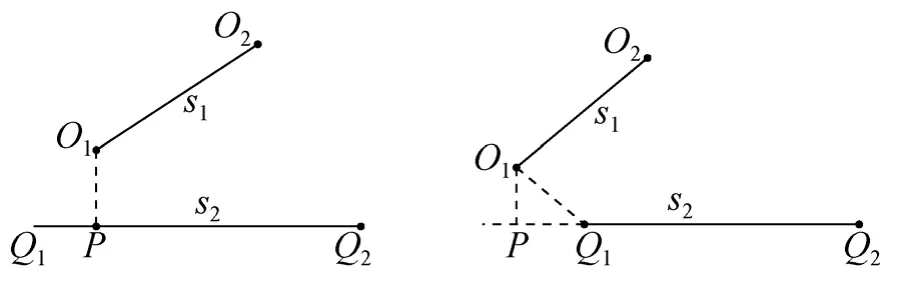
图1 线段间最小距离示意图
如图1所示,过s1的一端点O1作s2的垂线,有两种情况,分别为垂足P落在线段s2内和线段s2外。若垂足落在s2内,则s1到s2的最小距离为s1的一端点与它到s2的垂足之间的距离O1P;若垂足落在s2外,则s1到s2的最小距离为s1的一端点与s2的一端点间的距离O1Q1。因此,在求线段到线段的单向最小距离时只要求线段的端点到另一线段的最小距离即可。计算折线到折线的Hausdorff距离就转化为了计算点到线段的距离。
2.3 剪枝策略
参数曲线离散成为折线后,包含大量线段,而最后结果实际只产生在某两条线段中,若依次迭代所有线段进行计算,效率很低。因此本文采用一定的剪枝策略来提高计算效率。剪枝方法分为2个步骤:①画折线中每条相邻线段的角平分线,并计算角平分线与另一折线的交点来代替Voronoi图,因为线段集的Voronoi图是由这些角平分线与线段组成的,同时采用增量式算法将另一折线上的线段进行再分割,而每条线段的端点则作为计算的采样点;②判断每个采样点与角平分线交点的位置关系,找到对应的线段,计算时只需计算每个点到对应线段的距离,其他线段可作为无效线段排除。
2.3.1 排除d2上无效线段
在计算点到线段的距离时,为了找到与点相对应的距离最短的线段,需利用Voronoi图。根据Voronoi图的定义可知,在平面内折线d的Voronoi图划分的n个区域内,每个区域内包含d的一条线段,该区域内点到该线段的距离均不超过到其他线段的距离。但是由于线段集的Voronoi图的构建很复杂,因此,本文只求出d2上相邻线段的角平分线与折线d1的交点,并辅以增量式算法来定位对应线段,因为线段集的Voronoi图是由这些角平分线与线段构成的。d1中线段的端点出现在哪两条角平分线中间,该点对应的线段即为该两角平分线中间所夹的线段,计算时只要计算该点与该线段之间的最短距离,d2上其余线段可以排除。
该判断方法如图2所示,ss1与ss2的角平分线为t1,ss2与ss3的角平分线为t2,s1的端点O1在t1和t2之间,所以点O1对应的线段是ss2。只需计算点O1到线段ss2的最短距离,ss1和ss3被排除,不需要参与计算。
下面将介绍计算相邻线段的角平分线的具体方法。如图3所示,AB,AC是两条相邻线段,A,B,C的坐标已知,D是∠BAC的角平分线与BC的交点,DP,DQ分别是AB,AC上过点D的垂线,要求角平分线上点D的坐标(x,y)。
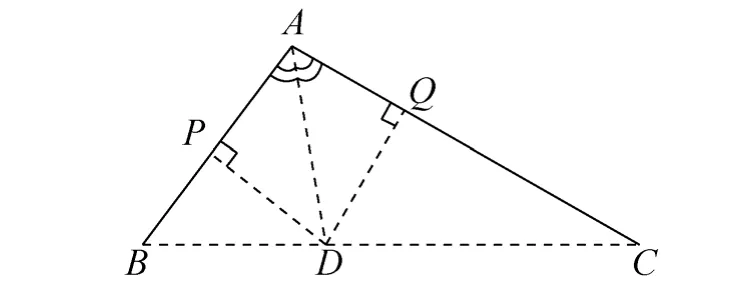
图3 角平分线算法示意图
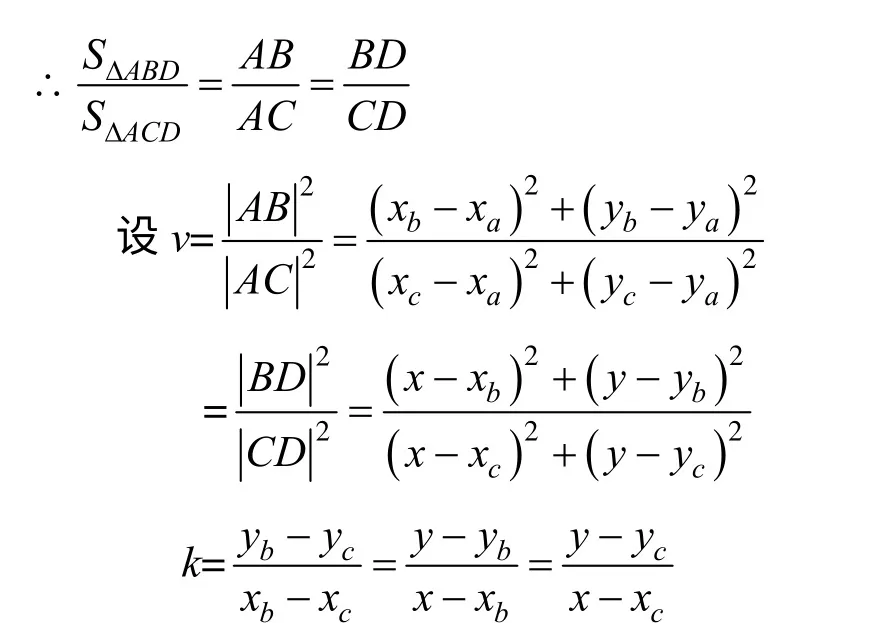
将k带入v,可得
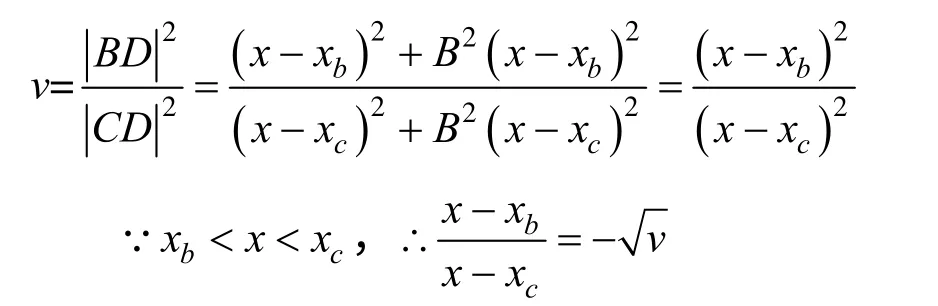
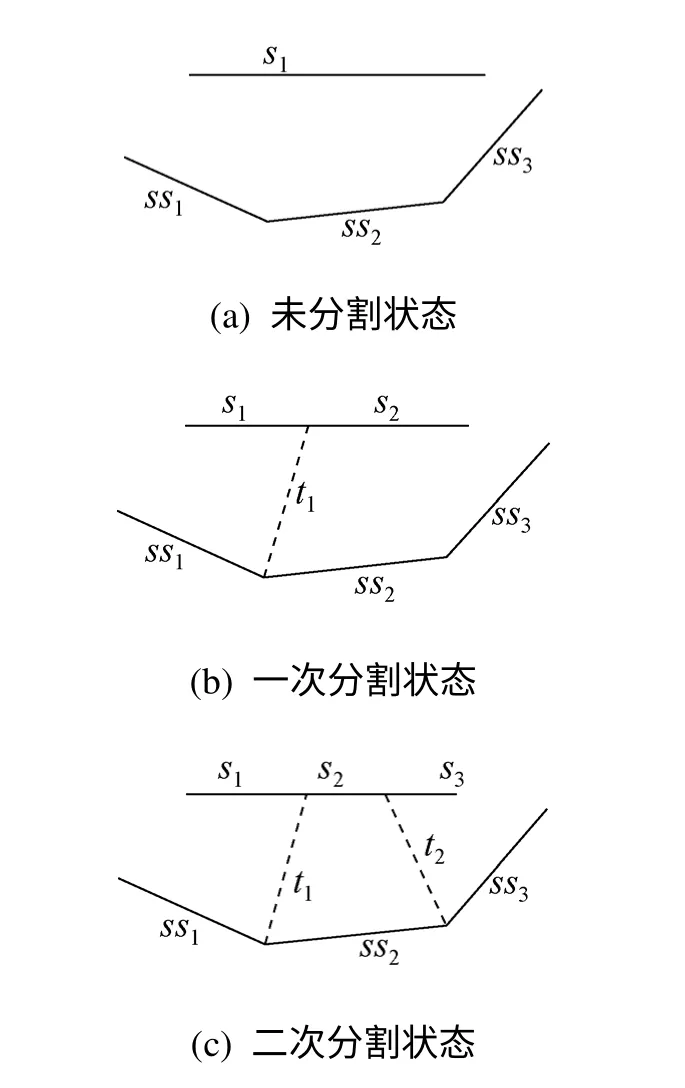
图4 增量式算法示意图
2.3.2 排除d1上无效点
在计算d1到d2单向Hausdorff距离的算法中,以d1中所有线段的端点为采样点,从d1的一端开始依次计算每个点到d2上相对应线段的最短距离。将d1上经过前i个点的折线记为d1(i),根据Hausdorff的定义可知下列关系成立:
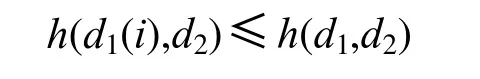
将h(d1(i),d2)记为lowerBound。接下来继续考察第i+1个点Pi+1,若d(Pi+1,d2)≤lowerBound,则第i+1个点Pi+1可被排除,h(d1(i+1),d2)仍然等于h(d1(i),d2),即 lowerBound的值不变;若d(Pi+1,d2)>lowerBound,则lowerBound被重新赋值为d(Pi+1,d2)。这个过程实际是不断提升下界lowerBound的过程,直至lowerBound正好等于h(d1,d2)。
3 实验结果
本文所提出的方法适用于所有参数曲线,在此处将其分别应用于B样条曲线和NURBS曲线并进行了实验。图5显示了参数变化量e分别为0.02,0.005和0.002的3组B样条曲线,并显示了曲线r1和r2间产生Hausdorff距离的点的位置以及该点所对应的线段,其中r1经过实心黑点,r2经过空心黑点,紫色圆点表示曲线上产生Hausdorff距离的点的位置以及该点所对应的线段。表1给出了对应的近似Hausdorff距离的计算结果,同时还给出了与未采用剪枝策略的计算方法在时间上的比较。

图5 B样条曲线实验结果对比图

表1 3组不同参数变化量的B样条曲线间的近似Hausdorff距离
图6显示了参数变化量e分别为0.02,0.005和0.002的3组NURBS曲线,并显示了曲线r1和r2间产生Hausdorff距离的点的位置及该点所对应的线段,其中曲线上第i个控制顶点的加权值取i除以5的余数,r1经过实心黑点,r2经过空心黑点,紫色圆点表示曲线上产生Hausdorff距离的点的位置以及该点所对应的线段。表2给出了对应的近似Hausdorff距离的计算结果,以及与未采用剪枝策略的计算方法在时间上的比较。

图6 NURBS曲线实验结果对比图

表2 3组不同参数变化量的NURBS曲线间的近似Hausdorff距离
从上面的实验结果可以看出,采用本文所介绍的角平分线与增量式算法相结合的剪枝策略,在计算Hausdorff距离时与未采用剪枝策略的计算方法相比,计算时间大大减少了。在参数变化量e越小时,即折线越逼近曲线时,速度优势体现的越为明显。
4 结论
本文首先从理论上论证了算法的合理性,并且对所有连续的参数曲线都是有效的,实验表明,本方法计算速度快,逼近度高,基本解决了参数曲线的Hausdorff距离的计算问题,可以在几何设计、图像匹配、图像识别等领域中广泛应用。
[1]Ahn Y J.Hausdorff distance between the offset curve of quadratic Bézier curve and its quadratic approximation [J].Communications-Korean Mathematical Society, 2007,22(4): 641-648.
[2]寿华好, 黄永明, 闫欣雅, 缪永伟, 王丽萍.两条代数曲线间Hausdorff距离的计算[J].浙江工业大学学报,2013, 41(5): 574-577.
[3]李英明, 李旭健.两条参数曲线间的Hausdorff距离的研究[J].华中师范大学学报(自然科学版), 2012, 46(3):270-274.
[4]Scharf L.Computing the Hausdorff distance between sets of curves [D].Diplomarbeit, Freie Universität Berlin,2003.
[5]Alt H, Scharf L.Computing the Hausdorff distance between curved objects [J].International Journal of Computational Geometry & Applications, 2008, 18(4):307-320.
[6]Elber G, Grandine T.Hausdorff and minimal distances between parametric freeforms in R2 and R3 [M].Springer Berlin Heidelberg, 2008: 191-204.
[7]Kim Y J, Oh Y T, Yoon S H, Kim M S, Elber G.Precise Hausdorff distance computation for planar freeform curves using biarcs and depth buffer [J].The Visual Computer, 2010, 26(6-8): 1007-1016.
[8]Chen Xiaodiao, Ma Weiyin, Xu Gang, Paul J C.Computing the Hausdorff distance between two B-spline curves [J].Computer Aided Design, 2010, 42(12):1197-1206.
[9]Chen Xiaodiao, Chen Linqiang, Wang Yigang, Xu Gang,Yong Junhai, Paul J C.Computing the minimum distance between two Bézier curves [J].Journal of Computational and Applied Mathematics, 2009, 229(1): 294-301.
[10]Chen Xiaodiao, Yong Junhai, Wang Guozhao, Paul J C,Xu Gang.Computing the minimum distance between a point and a NURBS curve [J].Computer-Aided Design,2008, 40(10): 1051-1054.
[11]白彦冰.自由曲线到自由曲线曲面Hausdorff距离近似值的计算[D].北京: 清华大学, 2011.
[12]Johnson D E, Cohen E.A framework for efficient minimum distance computations [C]//1998 IEEE International Conference on Robotics and Automation,Leuven, Belgium, 1998: 3678-3684.
[13]Belogay E, Cabrelli C, Molter U, Shonkwiler R.Calculating the Hausdorff distance between curves [J].Information Processing Letters, 1997, 64(1): 17-22.

