高压直流输电次同步振荡时域仿真分析与控制

，，

(西南交通大学电气工程学院，四川 成都 610031)

0 引 言

中国的能源资源非常丰富，但其分配极不均衡，煤炭资源80%集中在西部和北部，水资源80%集中在西南地区。但另一方面，随着中国经济的快速发展，用电负荷急剧增加，尤其是中国的东部经济发达地区，这一现状决定了必须采用大容量、超高压、远距离输电。[1]

高压直流输电具备损耗小、可以限制短路电流、线路造价低等优点，因而在远距离、大容量输电方面具有不可替代的优势。越来越多的电力系统采用交、直流互联电网[2-3]，由于大型受端电网的形成，近年来的系统规划已开始出现多条直流和多条交流线路并列运行的多馈入交直流混合输电系统。

但是高压直流输电(HVDC)线路和汽轮发电机组之间的相互作用会引起发电机轴系与电气系统以一个或多个低于同步频率交换能量而损坏的现象，从而引发次同步振荡现象。次同步振荡是一类严重的系统稳定性问题，不但会使系统产生振荡现象，而且极易造成汽轮发电机组的大轴损毁[2]。如何采取有效的措施抑制次同步振荡是电力系统中一项重要的研究内容。

文献[4]采用人工神经网络法对扭振系统的特征值进行实时分析，可用于在线分析次同步振荡(subsynchronous oscillation,SSO)；文献[5]采用多变量频域法对次同步振荡进行分析，可反映出发电机轴的不对称性；文献[6]采用开环系统频率特性法对汽轮机调节系统的SSO特性进行分析；文献[7]基于模态控制理论，利用特征值法设计次同步振荡抑制器(subsynchronous damping controller,SSDC)；文献[8]提出了一种基于传递函数的波特图设计SSDC参数的方法；文献[9]提出了与遗传算法相结合的SSDC设计；文献[10]提出了基于H∞控制理论的SSDC，提高了SSDC的在线计算速度，并使其具有一定的鲁棒性。

基于测试信号法，下面先介绍高压直流次同步振荡发生的原理，然后分析高压直流次同步振荡进行时域分析，最后根据高压直流次同步振荡抑制机理，设计SSDC，抑制次同步振荡。最后利用PSCAD/EMTDC软件在IEEE第一标准模型基础上，对其抑制效果进行了仿真验证。

1 高压直流次同步振荡机理

以图1所示的简化HVDC系统模型为例分析HVDC引发SSO时系统状态量的变化过程，HVDC整流侧在定电流或者定功率控制时引起的次同步振荡问题的状态量的变化过程见图2。若与整流站紧密耦合的发电机上转子机械角速度施加一个微小扰动Δθ(Δω)，则将导致机端电压 (即图2中的换流站换流母线电压处U∠θU)的相位θU和幅值U产生摄动，经交流线路从而该扰动传递到整流站换流母线上。现代的HVDC系统中换流器普遍采用EPC方式，对应于换流母线电压相位的摄动，换流阀触发角α将产生相同的摄动(Δα)，因此换相电压幅值以及触发角的改变，将会引起直流母线电压的Ud摄动，而该摄动会引起直流电流Id的变化，并进一步导致直流功率发生的变化(ΔPd)。这两者的作用将导致直流电压和电流偏离平衡状态，而HVDC定电流控制将感应这种偏差并加以快速校正和调整, 但是往往不能消除 (ΔId)，从而导致电流功率变化为ΔId′(ΔPd′)。直流功率的变化通过交流网络的传递将导致交流功率变化ΔPd′，从而导致发电机电磁力矩变化ΔTe，而ΔTe的变化又会最终又反馈作用于机组轴系。如果发电机转速的变化Δω与引起的电气转矩变化量相位滞后超过90°，则会将形成一种正反馈性质的轴系扭振相互作用，ΔTe不断助增摄动幅值，ΔTe会进一步增大初始扰动Δθ(Δω)，就会出现电气负阻尼。一旦该电气负阻尼超过发电机组轴系所提供的正机械阻尼，就出现HVDC控制系统引起的轴系扭振不稳定。

图1 准稳态模型所依据的换流器电路结构

图2 HVDC引发次同步振荡系统状态量变化过程

2 高压直流次同步振荡抑制机理

SSDC 作为抑制 SSO 有效而经济的手段，其控制性能受反馈信号的选取和控制方法的确定的影响，同时还应考虑其与其他设备控制特性的协调，在文献[11]中关于SSO产生机理的更全面解释中提到，负阻尼的实质是电磁转矩偏差对转子初始扰动产生助增作用，也就是说电磁转矩偏差与发电机轴系转速偏差之间的相位大于 90°，因此可以采用与 PSS 抑制低频振荡的原理相似的相位校正(phase correction, PC)来阻尼 SSO。也就是以发电机转速偏差或者频率偏差信号为反馈信号，经过放大和相位校正处理，其输出信号通过换流站控制回路提供一个附加的电磁转矩，使其与原有电磁转矩偏差的合成量与转速偏差之间的相位小于 90°(如图3所示)，使整个系统呈现出正的电气阻尼。

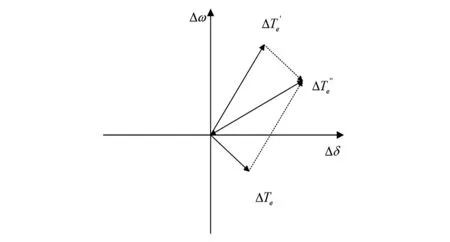
图3 电气转矩的向量关系图

3 HVDC次同步振荡分析

3.1 HVDC次同步振荡模型

如图4所示为含HVDC电力系统的典型简化模型，该模型包含存在次同步振荡现象的待研机组(图中虚框所示)，交流网络部分用无穷大电源S1和等值阻抗的串联组合并与整流侧连接，无穷大电源S2为逆变侧的受端系统。

该系统模型发电机及轴系模型的参数均采用IEEE第一谐振模型的参数，直流部分采用CIGER HVDC标准模型，S1和S2的额定频率均为60 Hz，端电压为26 kV，发电机的额定容量为892.4 MVA，直流额定输送功率为1 000 MW，额定电压为500 kV。

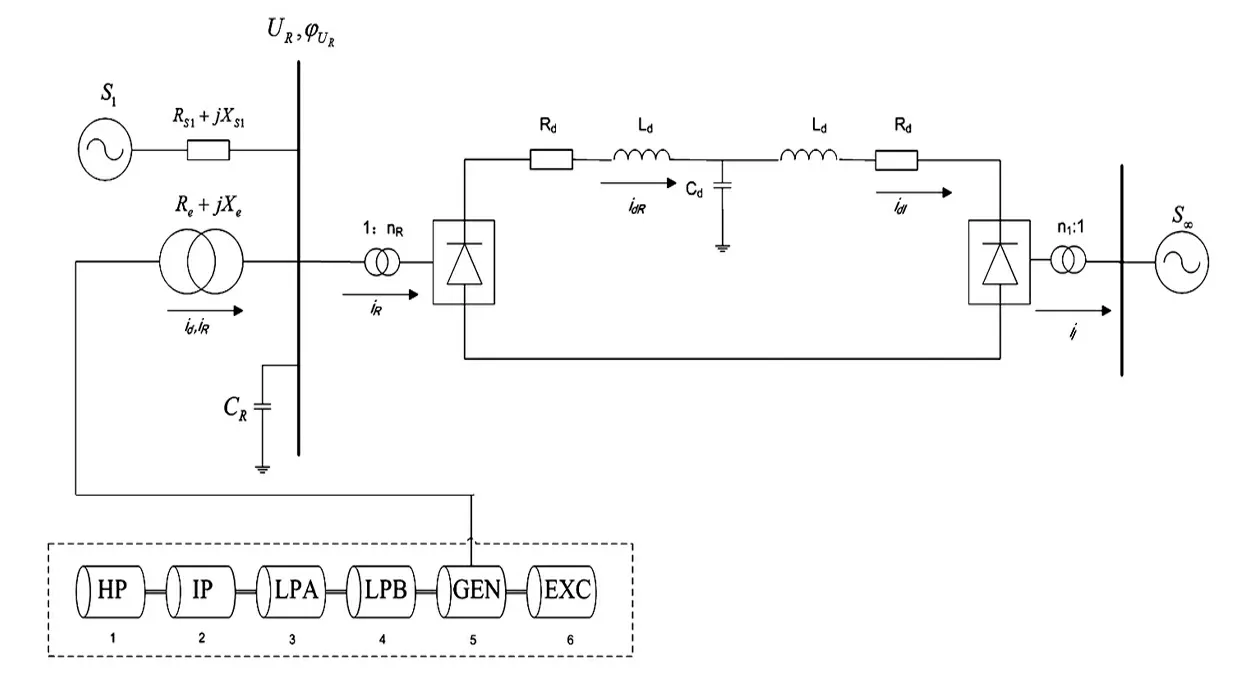
图4 含HVDC次同步振荡的典型简化模型

3.2 系统时域仿真分析

在PSCAD/EMTDC中建立图4的仿真模型，发电机轴系采用6轴段模型，机械阻尼设为0。待系统进入稳态后，在发电机出线上于2.5 s时给出三相接地故障，故障持续0.05 s后切除，仿真时间为20 s，发电机各个轴系质块扭矩将发生次同步振荡。

对发电机转速偏差进行FFT分析得到其各频率分量的幅值情况，如图5所示，可以看出幅值较高的频率均对应于发电机轴系的轴系振荡模态。其中幅值最高的为16 Hz，其次为32 Hz，25 Hz和20 Hz分量的幅值大小相近，而1 Hz和47 Hz分量的幅值非常小，可以忽略。

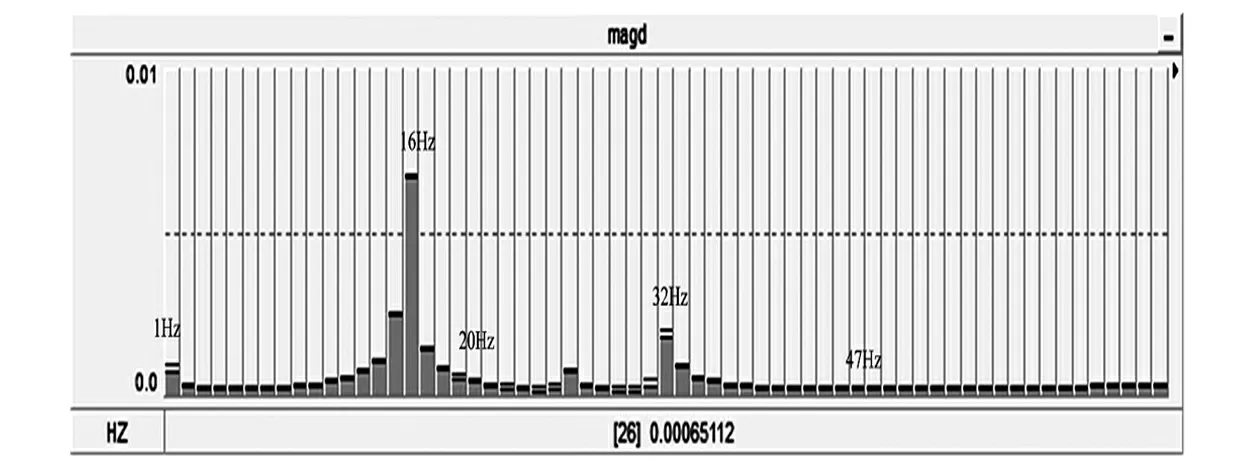
图5 发电机转速FFT分析

对发电机各质量块相对于发电机的机械位置和相对于额定转速度，各质量块角速度偏差进行仿真分析，如图6和7所示，各质量块相对于发电机的机械位置明显处于振荡状态，而且呈增大的趋势。相对于额定转速度，各质量块角速度偏差发散的趋势非常明显，这些都表明了次同步振荡对发电机组危害相当严重。

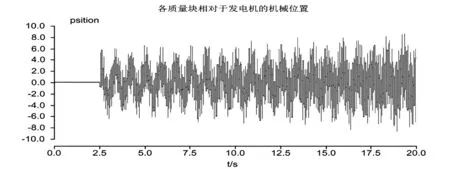
图6 各质量块相对于发电机的机械位置

图7 相对于额定转速度，各质量块角速度偏差

对发电机各轴段的扭矩、发电机转速度、电磁转矩进行仿真分析。如图6至图7得，在2.5 s施加扰动后，发电机各轴段的扭矩呈现发散现象，发电机转速与发电机电磁转矩呈现不稳定状态，系统发生次同步振荡。

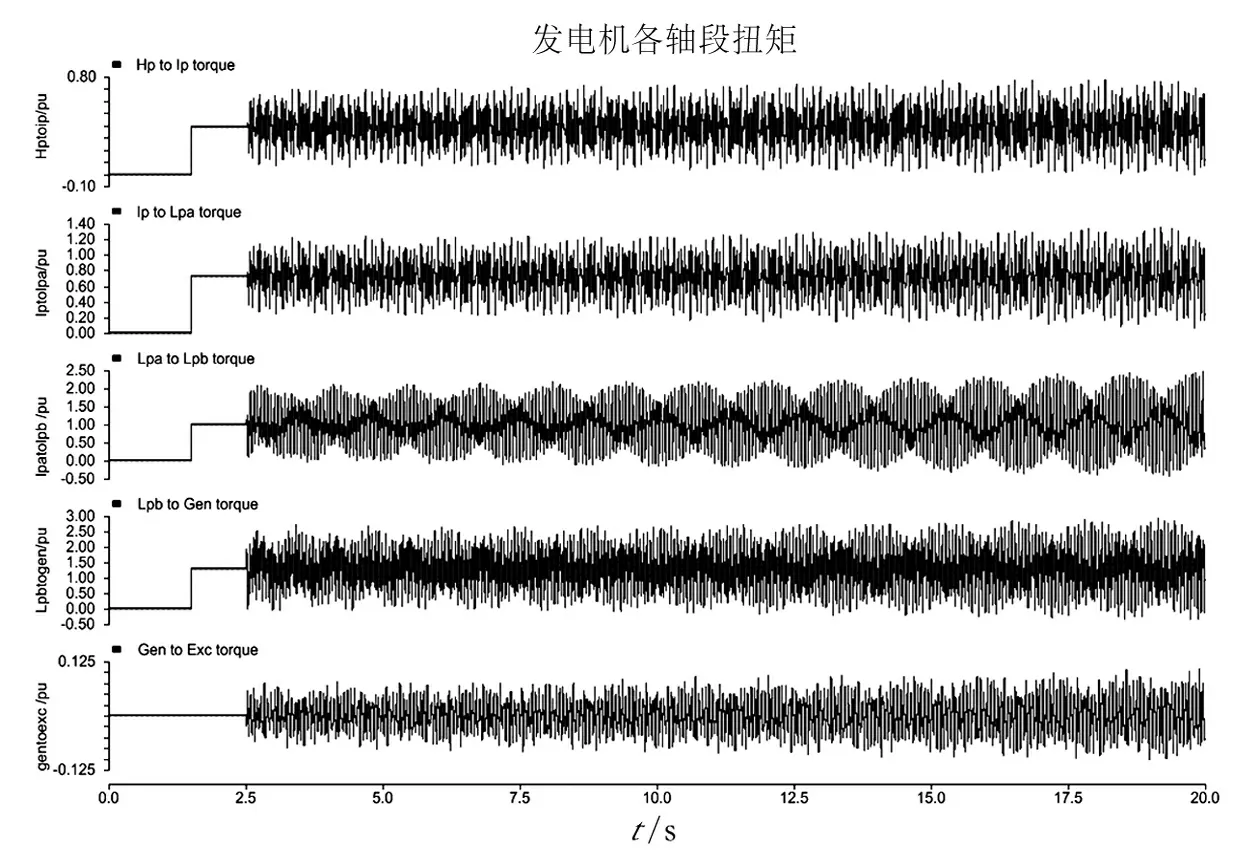
图8 发电机发生故障时各轴段间的扭矩

图9 发电机转速运行示意图

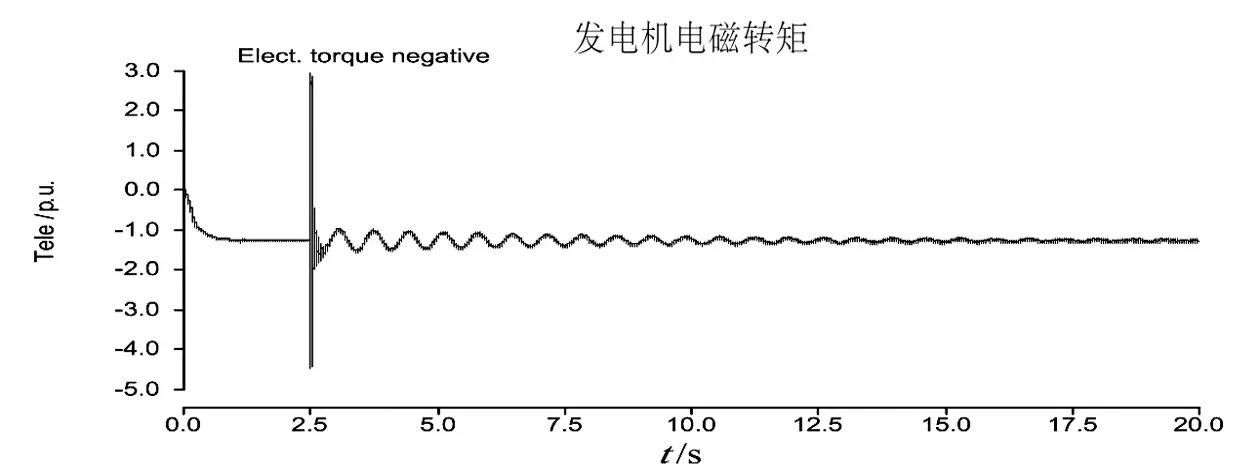
图10 发电机电磁转矩示意图

4 HVDC次同步振荡控制器设计

4.1 控制器SSDC设计原理

SSDC抑制SSO时需要向发电机组提供一个足够大的正阻尼力矩才能抑制发电机发散的转速振荡，因此SSDC的控制策略为：当发电机转速减小时，在SSDC的作用下HVDC的直流电流参考值减小，由于换流器的快速响应特性，直流功率减小，则发电机输出的电磁功率也将减小。对恒定的输入机械功率，电磁功率的增加将导致转子动能的增加，从而使得转子转速增加；反之，发电机转速减小时HVDC定电流参考值增加，则直流功率增加，发电机的电磁功率增加，从而使发电机转子减速。在HVDC换流器的快速响应特性下，通过SSDC的这种控制策略能增强发电机组的次同步振荡阻尼，达到抑制系统次同步振荡的目的。

4.2 控制器SSDC设计方案

以图4建立的模型为研究对象，其中，转子轴系6个轴段构成，6个轴段对应转子轴系6个扭振模式，除去一个刚体模式，进行 SSO 分析的有 5 个扭振模式，轴系的机械扭振模态频率分别为 15.71 Hz、20.21 Hz、25.55 Hz、32.28 Hz、47.45 Hz。由于在47.45 Hz处，该模态近似为等幅振荡模式，由于该分量所占比重非常小，所以在设计阻尼控制器时只用考虑前4个扭振模式。

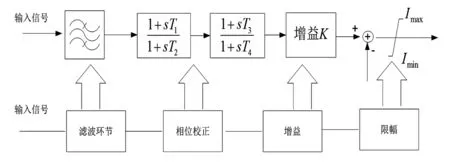
图11 SSDC结构示意图

这里SSDC采用以发电机的转速偏差Δω作为反馈信号，采用分模态控制的方法，经过4阶Butterworth滤波器，通过相位补偿环节补偿负阻尼所需要的相位差,最后经幅值增益和限幅环节得到电流补偿量将输出信号叠加至直流电流的整定值信号中，共同作为定电流控制器的输入信号，消除己产生的次同步振荡。

图12 发电机转速偏差为反馈信号的多模态阻尼控制器

SSDC各个模式的滤波及相补环节如表1。

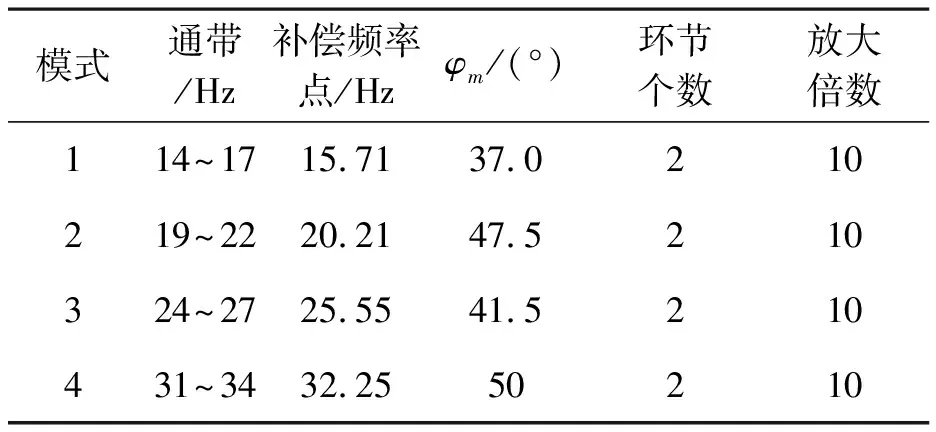
表1 SSDC参数

4.3 控制器SSDC抑制效果仿真分析

为进一步验证加入SSDC后，抑制次同步振荡的有效性，对图4所示模型加入SSDC进行仿真分析。待系统进入稳态后，在发电机出线上于2.5 s时给出三相接地故障，故障持续0.05 s后切除，仿真时间为20 s。

图13 加入SSDC时发电机发生故障时各轴段间的扭矩

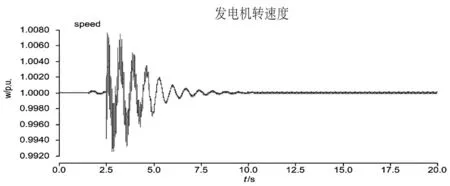
图14 加入SSDC时发电机转速度示意图

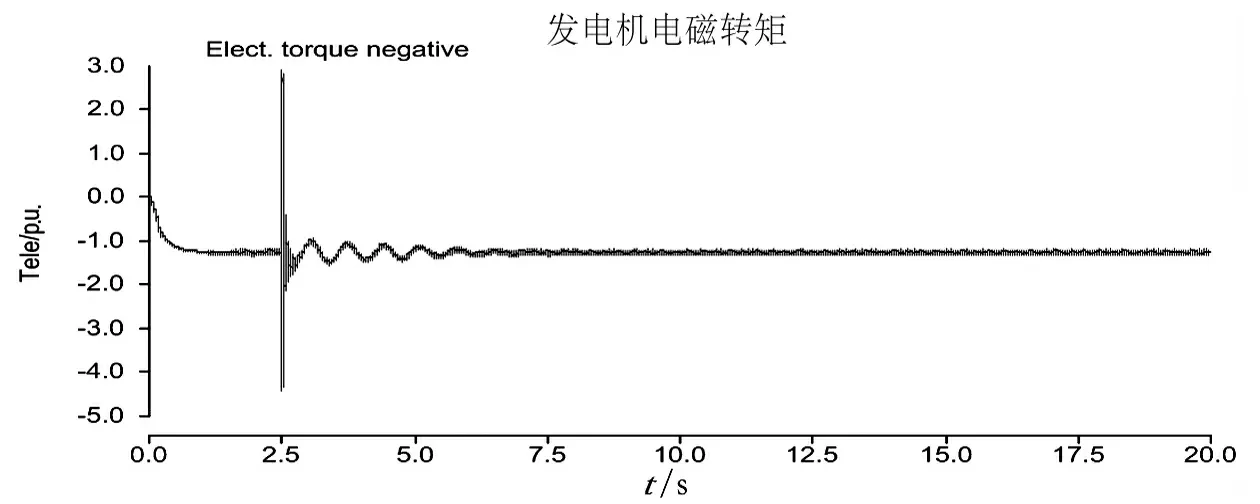
图15 加入SSDC时发电机电磁转矩示意图

由图13至图17可得，发电机各轴段扭矩、电磁转矩及发电机转速度等振荡都得到明显的收敛，次同步振荡得到了抑制。

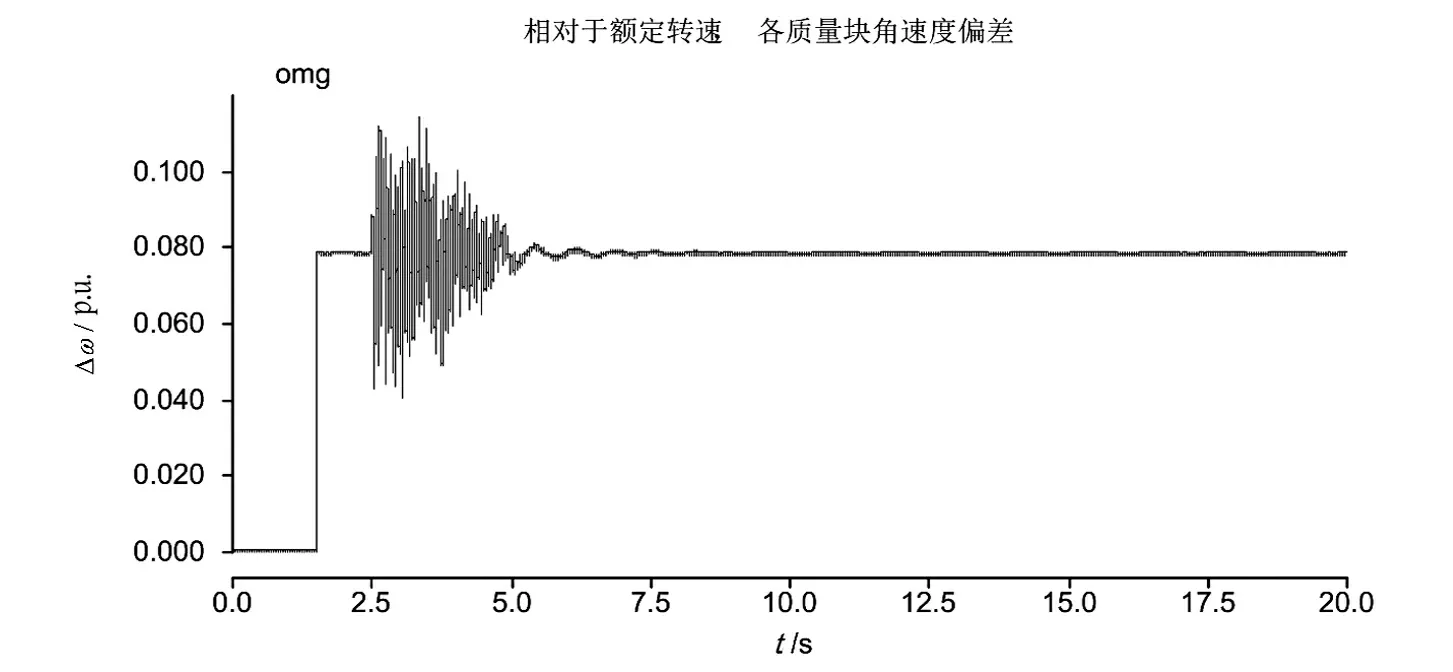
图16 加入SSDC相对于额定转速，各质量块角速度偏差示意图

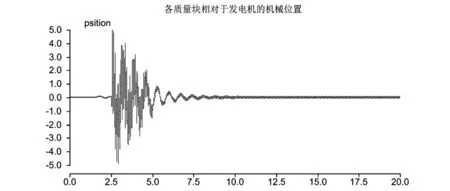
图17 各质量块相对于发电机的机械位置示意图

5 结 论

通过上述时域仿真分析，得出下列结论。

(1) HVDC系统的不正当控制将会引发次同步振荡现象，这将会引发系统发生故障乃至造成发电机损坏。

(2) 通过对发电机转速度进行FFT分析可得，系统发生次同步的最大振荡频率为15.6 Hz。

(3) 设计的次同步阻尼控制器都可以达到抑制 SSO 的目的，也就是说在轴系扭振模态频率处电气阻尼转矩系数为正就可以抑制次同步振荡。

[1] 张运洲，张卫东．国家电网公司电网“十一五”发展规划综述[N]．国家电网报， 2006-36-38(1).

[2] 赵遵廉．中国电网的发展与展望[J]．中国电力，2004， 37(1)：1-6.

[3] 于立宏．能源资源替代战略研究[M]．北京：中国时代经济出版社，2008：14-16.

[4] Hsu YY，Jeng I H．Analysis of Torsional Oscillations Using an Artificial Neural Network[J]. IEEE Trans．on EC．1992，7(4)：684-690.

[5] 陈陈．多变量频域法分析电力系统次同步振荡[J]．电力系统自动化，1989(5)：22-27.

[6] 于达仁，徐基豫．大型汽轮机调节系统的设计对轴系扭振的影响[J]．中国电机工程学报，1992，12(4)：35-39.

[7] YY．Hsu and L．Wang．Modal Control of an HVDC System For the Damping of Subsynchronous Oscillations[J]．IEE proeeedings，1989，136(2)：78-86.

[8] R．J．Piwko，E．VLarsen．HVDC System Control for Damping of Subsynehronous Oscillations[J]．IEEE Transactions on Power Apparatus and Systems，1982，101(7)：2203-2211.

[9] 江全元，程时杰，曹一家．基于遗传算法的HVDC附加次同步阻尼控制器的设计[J]．中国电机工程学报，2005(1)：87-91.

[10] 杨秀，王西田，陈陈．基于H∞鲁棒控制理论的高压直流输电系统附加次同步振荡阻尼控制设计[J]．电网技术，2006，30(9)：57-61.