当前气候变化下的雅库特中部地区土壤温度状况预测

Peter Permyakov，Stepan Varlamov，Pavel Skryabin，Yara Ckachkov

(1.俄罗斯科学院西伯利亚分院北极自然技术研究所，雅库茨克677010，俄罗斯;2.俄罗斯科学院西伯利亚分院 麦尔尼科夫冻土研究所，雅库茨克677010，俄罗斯)

0 Introduction

Acception of various optimal engineering solutions for managing by thermal regime in the basement of engineering structures requires improvement of mathematical models based on actual physical factors and the development of new software simulation.

At the moment there are extremely relevant questions of modeling thermal processes，taking into account climate change.Essence of mathematical modeling is to replace the original object to its“image”-mathematical model-and further study it using computational logic algorithms implemented on computers.Such a mathematical representation of the process is a versatile method of scientific knowledge，including per-mafrost.

The question of prognostication reliability is one of the most serious problems，regardless of the method of the forecast［1，8，2］.

The error of the prediction reliability F is composed of three types of errors:

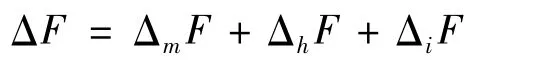
where ΔmF—the model error due to incomplete accounting factors;ΔhF—error due to statistical heterogeneity of influencing factors;ΔiF—instrumental error due to inexact measurement of influencing factors.

Practical analysis of the total error of thermal processes is determined mainly by two components:a model error ΔmF and heterogeneity error ΔhF，where the first one decreases and the second one increases with the number of factors considered［1］.Reliability of the prognostication depends on the quality of the data.

Evaluation of the thermal reaction of cryolithozone on climate change indicate a need for improved methods of quantitative geocryologicalprediction.

1 Materials and methods

Forecast of soil freezing and thawing is based on a mathematical model of heat transfer with phase transitions［2］.The classic statement of the problem(well known Stephen's problem)consists of the heat conductivity equation in thawed(Ωth)and frozen zones(Ωf) and two-leveled conditions on moving the interface of (ξ(τ))bound phases:

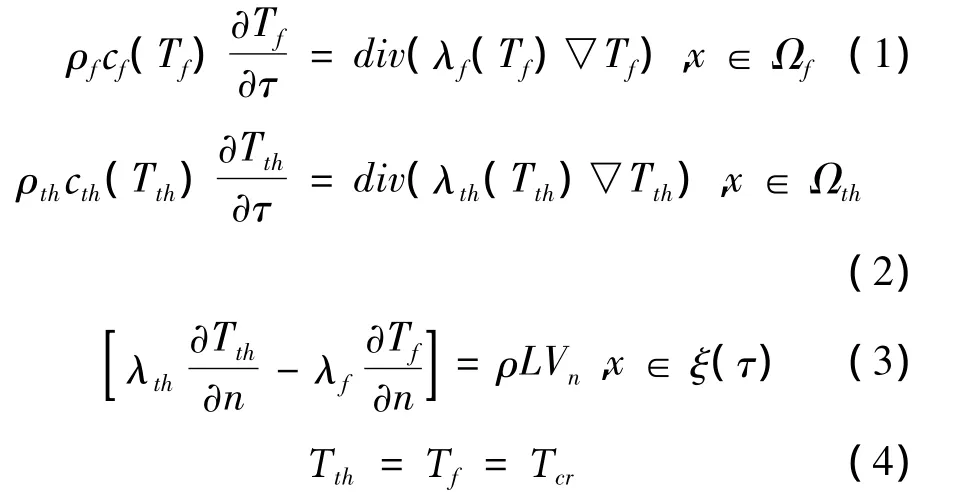
where T—temperature，℃;τ—time，s;x=(x1，x2， x3)—spatial coordinate;c—specific heat capacity，J/ kg;ρ—density，kg/m3;λ—thermal conductivity coefficient，W/(m·K);ξ(τ)—moving speed of the surface along the normal，m/s;Tcr—crystallization temperature of pore water，℃.

At the upper boundary of the studied area it is defined by the boundary condition of the III-kind for which the heat flux into the soil is determined by the convective heat exchange between the surface of rocks and the air:

here-Tai，Ts—the air temperature and soilsurface，respectively;∝ef—the effective coefficient of convective heat exchange with air，W/(m2·K).

The numerical realization of the problem(1)～(5)carried out an iterative implicit finite-difference scheme［3］.

In predicting ground temperature it is commonly used meteorological data averaged mean annual ambient temperature and snow depth.In recent years，due to global warming，there is a sharp change in the ambient temperature and snow depth.For a more accurate prediction it is used monthly meteorological data and the following technique.

Initial information on the temperature regime of air during the summer and winter periods is approximated by standard trigonometric function［4］:

where Ωas，Ωaw—the sums of positive and negative air temperature，K·s;τw，τs—duration，respectively，of the winter(average daily negative air temperature) and summer periods of the year，s;τ—time，s.

Similarly，the coefficient of convective heat transfer is approximated from the snow depth(Table 1).

Table 1 Thermal resistance and snow depth

As initial data we take heat balance observations data［5-6］at Chabyda monitoringsites(larch forest)，located in 20 km southwest from Yakutsk and Yakutsk (pine forest and a motley grass meadow)monitoring.Sites in Yakutsk have the same lithology and differ only in moisture content and vegetation.

2 Results and Discussion

Pine forest reduces the influx of solar energy to the soil surface，which helps to reduce heating and thawing.Therefore，in summer forest has almost always a cooling effect on the soil.In the pine forest humidity surface soil horizon is slightly greater than on a motley grass meadow，due to good water-holding capacity of forest the coverings.Conversely，soil horizons，located in the middle part of the active layer (range 0.6～1.2 m)，are often more dried up［5］.This horizon plays an important role in the temperature distribution in the depth mass.

The site of permanent Chabyda is located in a larch forestwith cranberry coveron sandy-loam soils［6-8］.Lithological section and thermal characteristics of the soils are presented in Table 2.

Table 2 Lithology and thermal characteristics of the soil

Numerical forecast covers the period from 1987 to 2012.This takes into account the monthly evolution of the snow cover，average daily temperature(Yakutsk weather station data)，as well as the heterogeneity of the ground mass.

Fig.1 shows the dynamics of the depth of thawing in the larch forest.General dynamics of thawing‘peaks’of numerical calculation and field observations coincide except for the initial period of observation，but the depth of thawing in the numerical calculation is growing，and the actual data-reduced.The reason may be that in the numerical calculation the dynamics of growth forest phytomass is not taken into account.

Similar results are presented for 25 years for the site in a pine forest(Fig.2).Calculations give low results.

Fig.1 Thawing depth in larch forest atChabyda site:1-field observations;2-calculated.

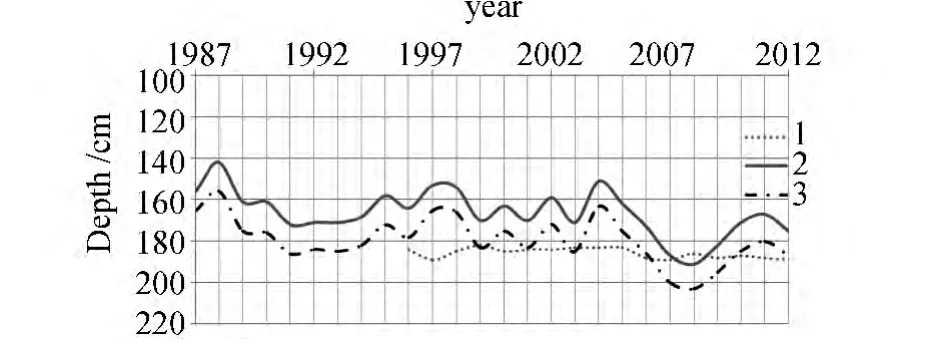
Fig.2 Dynamics depth of thawing in a pine forestat Yakutsk site:1-field observations;calculated:2-zero isotherm;3-0.3℃ isotherm

Fig.3 shows the comparative dynamics of the active layer depth of thawing on a motley grass meadow.The figure shows that the results of field observations are in satisfactory agreement with numerical calculations.

For example，Table 3 shows the comparative results of numerical calculations of the temperature field with the data of field observations in 2007，2011 and 2012.2007 is the warmest.The results of numerical calculation of grounds temperature on the sole of the annual layer of heat exchange in satisfactory agreement with the field data and a slight deviation is observed at the base of the active layer.

Fig.3 Dynamics of thawing depth on motley grass meadow at Yakutsk site:1-field observations;2-calculated

Table 3 Numerical results are compared with the data of the temperature field of field observations℃

Continued table 3

3 Conclusions

Thus，the algorithm is developed for solving onedimensional problem of freezing and thawing considering monthly snow cover dynamics，the average daily air temperature，as well as heterogeneity of the soil mass.A series of numerical calculations were carried out and comparison of results to field observations.Reliability of the forecast depends on the initial data.Analysis of the results shows satisfactory comparability calculations of the depth and thawing of soils temperature on the sole of the annual layer of heat exchange with the experimental data.The proposed algorithm can be applied to long-term prognosis geocryological.

［1］ Babich M D，Zavdiraka V K，Lyudvichenko V A.On the use of reserves of calculations optimization in computer technology solving applied and computational mathematics with the required quality characteristics［J］.Computational Mathematics and Mathematical Physics，2010，50(12):2 285-2 295.

［2］ Varlamov S P，Skachkov Y B，Scriabin P N.Ground temperature regime permafrost landscapes of Central Yakutia［M］.Yakutsk: Publishing House of SB RAS IMZ，2002.

［3］ Grechishchev S E.Optimal model natural processes the error and reliability［J］.Proceedings of the conference"Analysis and assessment of natural hazards in the building".Moscow.P，1997: 14-16.

［4］ Pavlov A V.Thermophysics landscape［M］.Novosibirsk:Nauka，1979.

［5］ Pavlov A V，Perlshteyn G Z，Tipenko G S.Actual aspects of modeling and prediction of the thermal state Cryolithozone in a changing climate［J］.Earth's Cryosphere，2010，(1):3-12.

［6］ Samarsky A A，Gulin A V.Stability of difference schemes［M］.Moscow:Editorial URSS，2005.

［7］ Scriabin P N，Varlamov S P，Skachkov Y B.Interannual variability of soil thermal regime Yakutsk region［M］.Novo-sibirsk:Publishing House of SB RAS，1998.

［8］ Feldman G M，Tetelbaum A S，Shender N I，et al.Manual on soil temperature forecast Yakutia［M］.Yakutsk:IMZ，1988.