逐步线性回归与神经网络预测的算法对比分析

谭立云，刘海生，谭 龙

(1.华北科技学院基础部，北京东燕郊 101601;2.武汉大学经济与管理学院，湖北武汉 430072)

0 引言

在计量经济学的学习中，探讨经济变量的关系常用回归分析方法，由于经济变量之间一般存在多重共线性，因此在建立多变量的回归方程的过程中，常需要进行各种检验，从理论上讲，只有通过了各种检验的方程才能得以使用。建立逐步回归方程是最常用的分析方法，能较好地克服多重共线性问题，建立一个真正实用的回归方程是一个非常复杂的过程。智能计算是现代数据分析的主要方法，是一种“黑箱”操作，虽然不像回归分析，有严格的数理推理，但由于模仿人的智慧过程，尤以神经网络算法为核心，得到的结果非常满意而得到了普遍的应用，各种智能算法得到了空前发展［1］。智能算法较回归分析方法而言，效果如何，从已经查阅的一些文献［2～7］中我们可以发现，一般都是用多元线性回归方程与BP神经网络相比较，看其预测效果，大都表现为神经网络预测精度高。逐步回归分析跟神经网络的其他改进类型的神经网络相比较预测效果又怎么呢，从查阅的文献中几乎没人进行研究，这正是本文要探讨的问题，本文的算例是易丹辉教授主编的《数据分析与EVIEWS应用》一书中的实例［8］，所用的智能算法［9～10］是BP神经网络、RBF径向神经网络和ELM极限学习机网络，所用的计算软件是Matlab神经网络工具箱。下面对这些理论做一个简单的论述。

1 逐步回归理论

多元逐步回归分析是指有两个或两个以上的自变量或者至少有一个线性解释变量的回归分析，分析模型的表达式为:

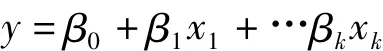
式中:β0为回归常数;βk为自变量xk的偏回归系数，k为自变量的个数，式中的偏回归系数和回归常数的数值通过样本的数据分析计算获得。

多元逐步回归分析的基本步骤是逐个引入自变量，每次引入对Y影响最显著的自变量，并对方程的老变量逐个进行检验，把变化不显著的变量逐个从方程中剔除掉。

逐步回归是逐步筛选自变量的回归，筛选过程是有进有出。开始时，将因变量与每一自变量作一元回归，挑出与因变量相关最密切或检验最显著的一元线性回归方程式。然后再引入第二个变量，原则是它比别的变量进入模型有更大的检验值。同时对原来的第一个变量作检验，看新变量引入后老变量还是否显著，若不显著则予以剔除。如此继续下去，每次都引入一个在剩余变量中进入模型有最大检验值的变量，每次引入后又对原来已引入的变量逐一检验以决定是否剔除，这样直到再无新变量可以引入，同时再无旧变量可以剔除为止，最终建立起逐步线性回归预测方程。

2 BP神经网络基本理论

人工神经网络(简称ANN)是对生理神经网络的抽象、简化和模拟，ANN作为一种并行分散处理模式，具有非线性映射、自适应学习和较强容错性的特点。

BP神经网络是基于误差反向传播算法的一种多层前向神经网络，BP算法作为人工神经网络的一种比较典型的学习算法，主要结构是由一个输入层，一个或多个隐含层，一个输出层组成，各层由若干个神经元(节点)构成，每一个节点的输出值由输入值、激活函数和阈值决定，网络的学习过程包括信息正向传播和误差反向传播两个过程。在正向传播过程中，输入信息从输入层经隐含层传到输出层，经激活函数运算后得到输出值与期望值比较，若有误差，则误差反向传播，沿原先的连接通路返回，通过逐层修改各层神经元的权值，减少误差，如此循环直到输出的结果符合精度要求为止。理论上已经证明，具有三个隐含层的三层网络可以逼近任意非线性函数。

目隐含层的激活函数多采用S型传递函数，输出层的神经元多采用线性传递函数。BP网络的存储信息主要体现在两个方面，一是网络的体系结构，即网络输入层、隐含层和输出层节点的个数;二是相邻层节点之间的连接权值。影响网络结构的主要参数是隐含层的节点个数、学习率lr和系统误差。.输入层和输出层节点个数由问题本身决定，一般来说是确定的，而隐含层节点个数由用户凭经验决定，或通过经验公式试算，个数过少，将影响到网络的有效性，过多会增加网络训练的时间。学习率通常在0.01～0.9之间，一般来说，学习率越小，训练次数越多，但学习率过大，会影响网络结构的稳定性。

具体的步骤简述如下:

1)BP网络的初始化，确定各层节点的个数，将各个权值和阈值的随机初始化;

2)输入样本和相应的输出，对每一个样本进行学习，即对每一个样本数据进行步骤3到步骤5的过程;

3)根据输入样本算出实际的输出及其隐含层神经元的输出;

4)计算实际输出与期望输出之间的差值，求输出层的误差和隐含层的误差;

5)根据误差更新输入层－隐含层节点之间、隐含层－输出层节点之间的连接权值;

6)求误差函数E，判断E是否收敛到给定的学习精度以内，如果满足，则学习结束，否则转向2)继续学习，直到满足停止学习的条件。

3 RBF径向神经网络基本理论

根据生物神经元具有局部响应的特点，将径向基函数技术引进神经网络产出了RBF神经网络。RBF网络的基本思想是:用RBF作为隐藏层空间，隐含层对输入层矢量进行变换，将低维的模式输入数据变换到高维空间内，使得在低维空间内的线性不可分问题在高维空间内线性可分。RBF神经网络结构简单、训练简洁而且学习收敛速度快，能以任意精度全局逼近任意非线性函数，可以更好地处理系统内在的难以解析的规律性，是对BP网络的一种改进，广泛应用于时间序列预测、模式识别、非线性控制和图形处理等领域。

RBF神经网络结构包括输入层、隐含层和输出层。其中，输入层将输入矢量直接映射到隐空间，起到传输信号的作用;隐含层含有若干隐单元节点，节点数量视具体求解问题而定。隐含层对网络输入做出非线性映射，映射函数即RBF，是一个径向对称、双方向衰减的非负非线性函数;输出层则对隐含层的输出采用线性加权求和的映射。由此可见，RBF神经网络是线性和非线性的有机统一，即从输入层到隐含层是非线性映射，采用的是非线性优化策略，学习速度较慢;而从隐含层到输出层则是线性变换，采用的是线性优化策略，学习速度较快。

RBF神经网络隐含层的激活函数采用径向基函数，通常定义为空间任一点到某一中心之间欧式距离的单调函数。最常用的径向基函数是高斯函数，公式为:

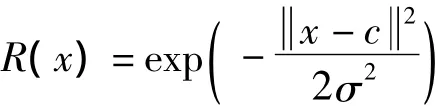
其中c为高斯函数的中心，σ2为高斯函数的方差。

理论上已经证明，一个RBF网络，在隐含层节点足够多的情况下，经过充分的学习，可以以任意精度逼近任意非线性函数，而且具有最有泛函数逼近能力，另外它具有较快的收敛速度和强大的抗噪和修复能力。理论上，RBF和BP都可以以任意精度逼近任意非线性函数，但由于它们使用的激励函数不同，其逼近性能也不同，Poggi和Girosi已经证明，RBF是连续函数的最佳逼近，而BP网络不是，此外，BP网络训练时间较长，容易陷入局部最优解，并且BP网络隐含层节点的数目依赖于经验和试算，很难取得最优网络，而RBF网络很大程度上克服了以上缺点，RBF网络采取局部激励函数学习速度比BP网络提高上千倍，其隐含层的节点在训练中确定，其收敛性也较BP容易保证，因而可以得到全局最优解。

4 ELM极限学习机基本理论

前馈BP神经网络大多采用梯度下降方法，该方法存在以下几个方面的缺点:(1)训练时间慢，由于梯度下降法需要多次迭代以达到修正权值和阈值的目的;(2)容易陷入局部极小点;(3)对学习率的选择敏感。因此，探索一种训练速度快、获得全局最优解，且具有良好的泛化性能的训练算法是提升前馈神经网络性能的主要目标，其中ELM极限学习机是单隐含层前馈神经网络(SLFN)的一种改进的新算法，该算法2006年由南洋理工大学黄广斌副教授提出，算法随机产生输入层与隐含层的连接权值及隐含层神经元的阈值，且在训练过程中无需调整，只需要设置隐含层神经元的个数，便可以获得唯一的最优解。与传统的训练方法相比，该方法具有学习速度快、泛化性能好的优点。

该算法是源于 Huang等人提出的下面的定理:

定理:给定任意Q个不同样本(xi，ti)，其中xi∈Rn，ti∈Rm，给定任意小误差ε＞0，和一个任意区间无限可微的激活函数g:R→R，则总存在一个含有K(K≤Q)对个隐含层神经元的SLFN，在任意赋值ϖi∈Rn和bi∈R情况下，有||Hβ－T＇||＜ε，其中 β为隐含层与输出层间的连接权值矩阵。

ELM学习算法主要过程分为三步:

1)确定隐含层神经元个数，随机设置输入权值ϖ及偏置;

2)选择一个无限可微函数作为隐含层神经元的激活函数，进而计算隐层输出矩阵H;

3)计算输出权值β。极限学习机网络最明显的缺点是隐含层节点数目一般较多(默认为训练样本数目)，势必造成网络的计算速度大大降低，因此适当选择隐含层节点数目也是一个难点。

5 算例分析

为了对比分析逐步线性回归与神经网络算法的预测精度，我们选用易丹辉教授主编的《数据分析与EVIEWS应用》中的一个案例，该例给出了1950年到1987年美国机动车汽油消费量Y (单位:千加仑)、汽车保有量X1(单位:辆)、机动车汽油零售价格X2(单位:美元/加仑)、人口数X3(单位:千人)和国民生产总值GNPX4(单位: 10亿美元)，具体数据见该书第二章第三节的案例2.1，要求用多元线性回归方法回归拟合QMG与MOB、PMG、POP、GNP之间的关系。这是一点典型的违背多元线性回归条件的案例，具有多重共线性、异方差和自相关性。

我们采取逐步回归尽量消除其影响，利用Matlab数值计算软件，最后我们得到的逐步回归方程是:

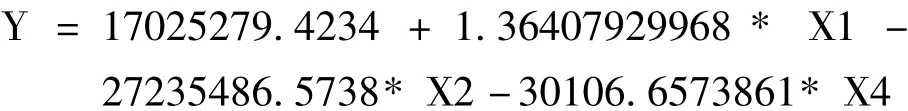
逐步回归方程中删除了人口数变量，说明这个变量是多余的。利用得到的回归方程进行了预测。

利用Matlab神经网络工具箱，上面介绍的三种神经网络智能算法都能很方便地实现，编写相应的计算程序，对原始数据归一化，以Y为输出变量，X1、X2、X3、X4为输入变量，分别采用BP神经网络(隐含层取6)、RBF径向基神经网络(扩展系数取0.3)和极限学习机网络(隐含层取6)对这些数据进行了拟合，网络训练时采取前33个数据进行训练，后5个数据用来进行测试，四种拟合方法的相对误差见表1。

四种预测值的对比见图1，四种预测方法的相对误差对比见图2。

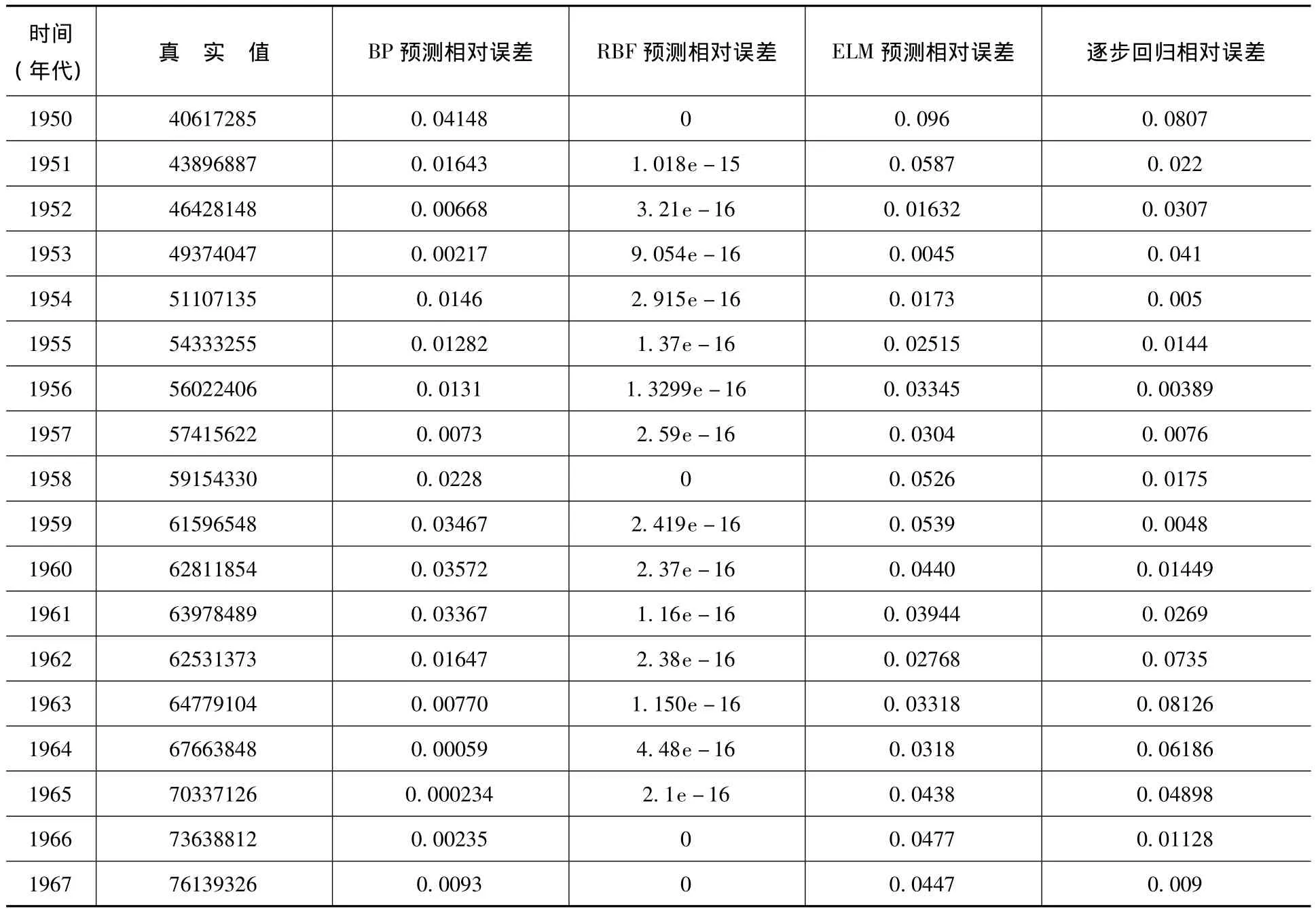
表1 BP预测、RBF预测、ELM预测、逐步回归预测误差比较

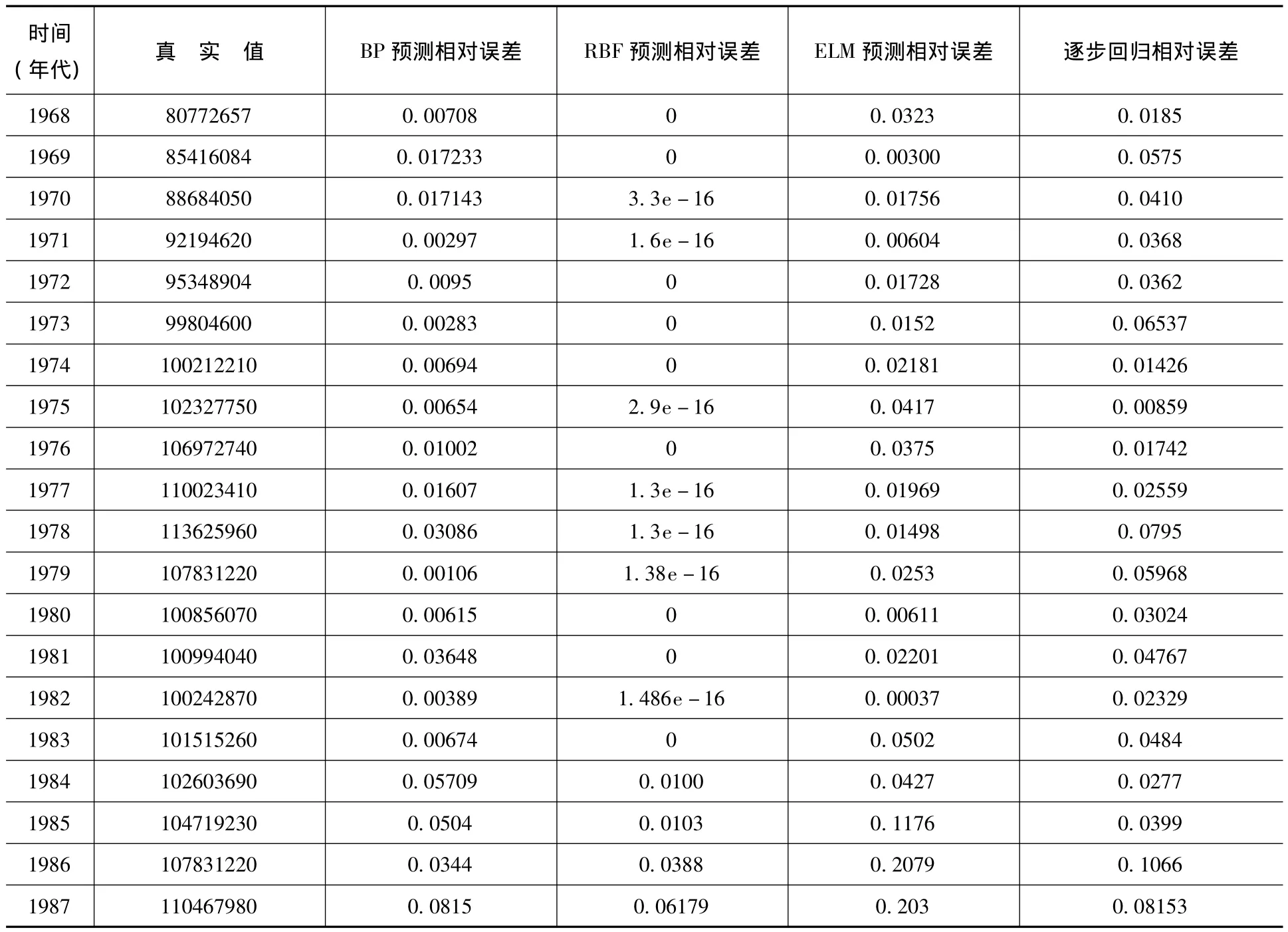
续表

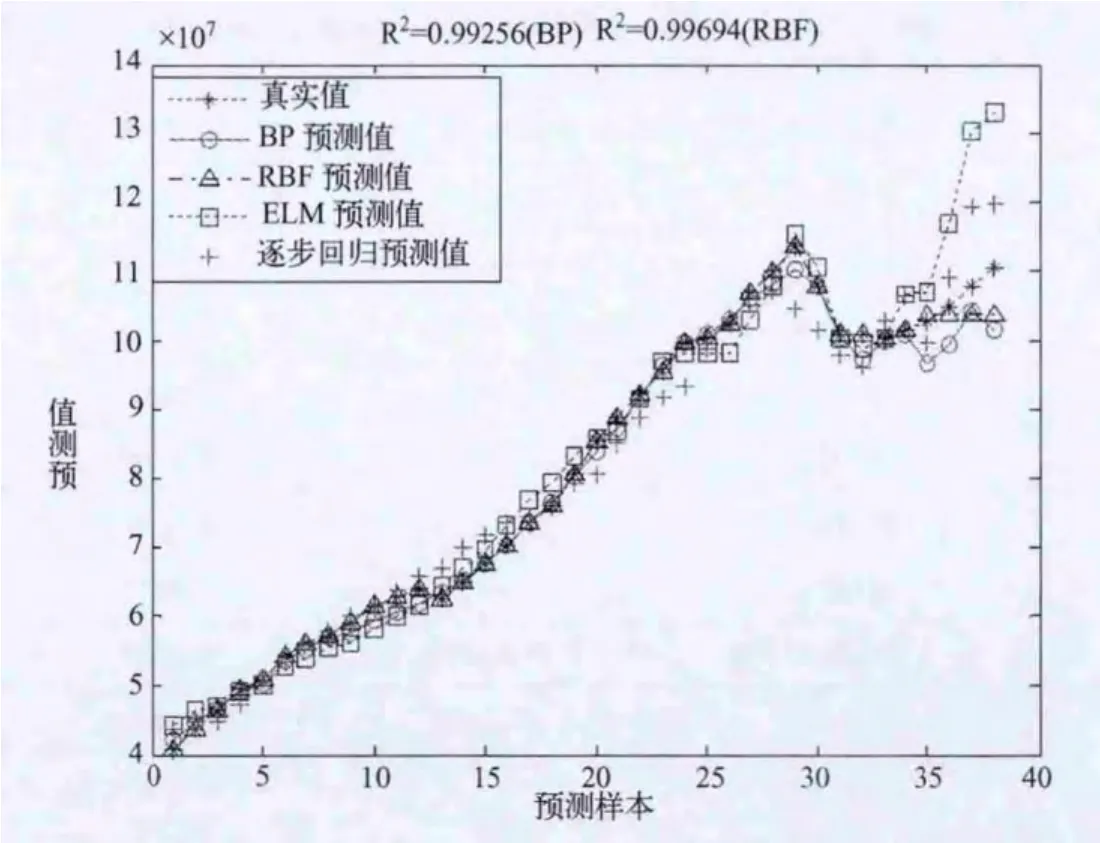
图1 真实值、BP预测、RBF预测、ELM预测、逐步回归预测对比图

从图1和图2可以看出:预测精度上RBF径向基神经网络预测效果最好，然后是BP神经网络的预测、逐步线性回归，ELM极限学习机预测的效果相对最差，但总体来说预测效果都比较好。按理ELM极限学习机网络应该预测效果BP更好，但如前所述，ELM网络对隐含层节点个数依赖较强，而且越接近训练样本个数越好，但我们这里只选取了6个隐含层节点，因此预测效果反而不如同样隐含节点个数的BP网络。

BP神经网络、RBF径向基神经网络、极限学习机网络和逐步回归总的均方误差分别为

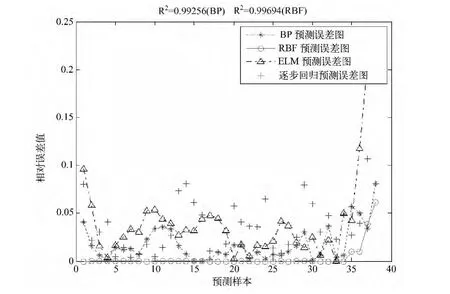
图2 BP预测、RBF预测、ELM预测、逐步回归预测相对误差对比图

1.0 e+013* ［0.5738，0.1747，3.6532，1.7029］。复相关系数分别为［0.9926，0.9969，0.9502 0.9669］，从这两个指标来讲，也可以推断上述结论。

6 结论

本文利用一个实例分别进行了逐步线性回归、BP神经网络、RBF径向网络、ELM极限学习机预测，想从中探讨统计方法与智能算法在预测精度上的差异，研究表明:

1)在数据拟合预测中，BP神经网络改进的RBF网络在预测精度上高于其他方法;

2)智能算法和回归方法相比，能够将复杂系统中的关系(线性或非线性)更精确地表达，预测效果好于回归方法;

3)BP神经的改进的极限学习机对隐含节点个数依赖较大，隐含节点个数与BP相同时，效果稍微比BP弱，但隐含节点个数增加时明显强于BP网络，仍稍弱于RBF网络。

4)本文研究仅是以一个典型的违背多元线性回归为案例，虽然神经网络方法在这个案例应用中获得了较满意的应用效果，这个研究结果是否具有普适性还有待进一步探讨。而且要从理论上来进行论证是非常困难的，也正是由于传统方法的不足才产生了各种智能仿生算法，而且其应用远远好于传统方法，相信随着研究和应用的深入，智能算法会得到更大更广的发展空间和应用领域。

［1］ 张睿，等.计算智能方法及应用研究［J］.电脑开发与应用，2012，(10):1－3.

［2］ 张晓瑞，等.基于RBF神经网络的城市建成区面积预测研究—兼与BP神经网络和线性回归对比分析［J］.长江流域资源与环境，2013，(6):691－697.

［3］ 张爱茜，等.运用回归分析与人工神经网络预测含硫芳香族化合物好氧生物降解速率常数［J］.环境科学，1998，(1):37－40.

［4］ 袁健.改进多元回归法与神经网络应用于水质预测［J］.水资源保护，2008，(3):46－48.

［5］ 金健，等.金融危机下的房地产业资本结构影响因素实证研究—多元线性回归模型与神经网络模型的比较［J］.商场现代化，2009，(8):88－91.

［6］ 吴玉鸣，等.中国粮食生产的多元回归与神经网络预测比较［J］.华东师范大学学报(自然科学版).2003，(4): 73－79.

［7］ 封铁英，等.企业资本结构及其影响因素的关系研究—多元线性回归模型与神经网络模型的比较与应用［J］.系统工程，2005，(1):42－47.

［8］ 易丹辉.数据分析与EVIEWS应用［M］.北京:中国人民大学出版社，2012.

［9］ 王小川，等.Matlab神经网络43个案例分析［M］.北京:北京航空航天大学出版社，2013.

［10］ 史峰，等.Matlab智能算法30个案例分析［M］.北京:北京航空航天大学出版社，2011.