基于遗传算法的模糊综合评价法在地下水质评价中的应用

夏哲兵，刘国东，任玉峰，刘 刚

（1.四川大学水利水电学院，四川 成都 610065；2.四川大学水力学与山区河流开发保护国家重点实验室，四川 成都 610065）

模糊综合评价法以其理论严谨、计算简单、评价较客观等特点被广泛应用，但其权重的确定仍具一定的经验性。目前模糊综合评价的研究难点之一就是如何科学地、客观地将一个多指标问题综合成一个单指标形式，以便在一维空间中实现综合评价，其实质是如何合理地确定这些评价指标的权重［1-2］。而层次分析法（AHP） 是目前一种被广泛应用的确定权重的方法，但它自身存在的主要问题是如何构造、检验和修正判断矩阵的一致性和计算判断矩阵各要素的权重［3］。

基于上述分析，笔者提出一种利用模糊综合评价矩阵构造适用于确定指标权重的判断矩阵，构建了利用遗传算法解决判断矩阵的一致性检验、修正和计算权重的新模型，并将此模型应用于地下水质评价工程实例中。

1 基于遗传算法的模糊综合评价法

假定共有m个井的水样资料，每个水井监测资料中有n个评价因子，以此来说明基于遗传算法的模糊综合评价模型的具体建模过程，主要步骤如下。

1.1 步骤1：构建评价指标

地下水质评价指标一般有总硬度、溶解性总固体、硫酸盐、硝酸盐、亚硝酸盐、氯化物、氟化物、铁和锰等，从上述指标中选取其中的n个构成评价指标。

1.2 步骤2：标准化及构造模糊综合评价矩阵

在实际应用中，因多数地下水质评价指标都存有量纲。为确定单个评价指标的相对隶属度，需对各指标进行标准化和无量纲化处理。为尽可能保持各评价指标值的变化信息［4］，且大多数地下水水质指标是越小越优，故按如下公式处理：

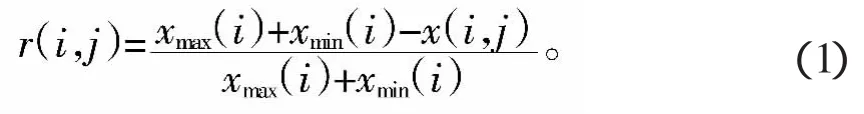
式中：x（i，j）为第j个水样中第i个评价指标的实测值；xmax（i）、xmin（i）和xmid（i）分别为第i个指标的最大、最小和中间值；r（i，j）为x（i，j）标准化后的数值，也叫做相对隶属度值，i=1～n，j=1～m。由计算出的r（i，j）作为矩阵元素，构建模糊评价矩阵R=（r（i，j））n×m。

1.3 步骤3：构造判断矩阵

为减少甚至避免信息的不对称，引入各评价指标的样本标准差。样本标准差用公式（2）表示，其可体现各评价指标之间的差异和反映评价指标对综合评价的影响程度，根据公式（3）可构造判断矩阵B［5］。

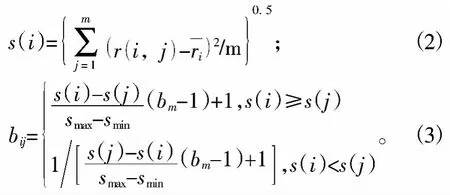
式中：bij为判断矩阵B中的元素；bm为相对重要性程度参数值；smax为s（i）中最大的数；smin为s（i）中最小的数。bm=min{9，int［smax/smin+0．5］}，min为取最小值函数，int为取整函数。

1.4 步骤4：权重计算过程

判断矩阵B的一致性检验、修正及其权重的计算，要求满足ai＞ 0和Σai=1 （i=1～n）。根据判断矩阵B的定义，理论上有［5］：

试验数据采用Excel2007进行整理。整理后数据采用SPSS17.0统计软件进行One Way Anova方差分析。

此时，B应具有性质［5-6］：①bii=ai/ai=1；②bji=aj/ai=1/bij（i，j=1～n）；③bijbjk=（ai/aj）（aj/ak）=ai/ak=bik（i，j，k=1～n）。其中：①单位性；②倒数性；③传递性，也为①与②的充分条件。

现在的问题就是用已知判断矩阵B，来推求各评价指标的权重值ai。若判断矩阵B满足公式（4），决策者能精确度量ai/aj，即bij=ai/aj，判断矩阵B具有完全的一致性，则有［7］：

在现实评价系统中，具有完全满意一致性的判断矩阵是几乎不存在的。在实际应用时，只需判断矩阵B满足一定精度要求，即满足一致性（CIC（n） ＜0．1） 即可。如果B不满足上述要求，则需根据实际情况进行修正。假定修正后的判断矩阵用Y表示，修正后的判断矩阵的权重值仍为ai，则称使公式（6）最小的Y矩阵为B的最优一致性判断矩阵［3］。

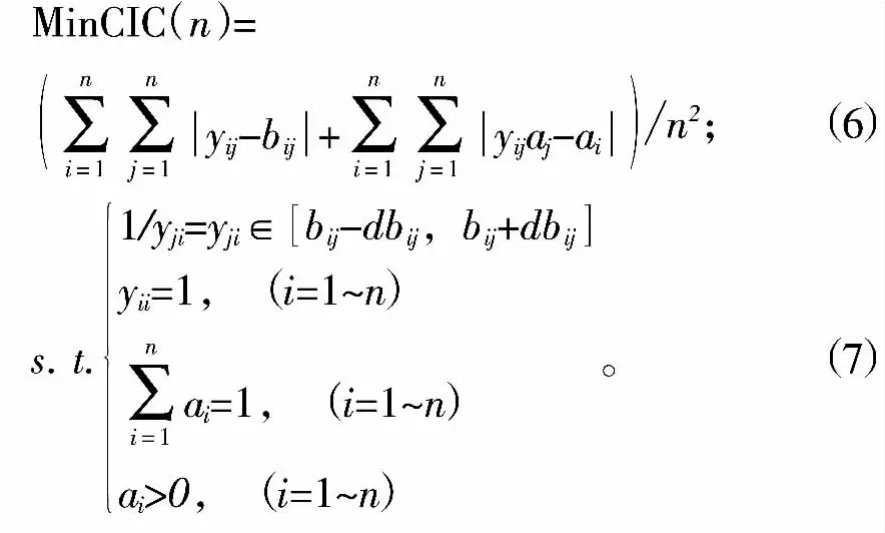
公式（6） 中的目标函数CIC（n） 为一致性指标系数，公式（7）为约束条件。d是不小于0的参数，可根据经验，按从小到大的原则从（0，0．25］内进行选取。

从公式（6）可以看出，目标函数是一个较复杂的非线性优化函数，非常规数学方法是可以解决的。其中权重值ai和修正判断矩阵Y的上三角矩阵元素均为优化变量，对n阶判断矩阵B而言，共有n（n+1）/2个独立的优化变量［7］。基于遗传算法具有出色的全局寻优功能，用它来求解公式（6）较为简单。遗传算法的步骤可参见文献［2］。

1.5 步骤5：模糊综合评价计算

通过遗传算法计算出最优解即为各评价指标的权重，将权重向量矩阵与模糊评价矩阵R进行复合运算，即求得地下水质综合评价结果矩阵Z。

式中：运算符号“·”为矩阵乘法，即把权重值与相对隶属度相乘并累加。综合评价值z（j）越大，说明第j个水样井的水质越好，据此可对地下水质的优劣做出科学的评价。

2 实例应用

2.1 研究区概况

本次研究区域位于内蒙古鄂尔多斯的乌审旗图克镇，地处毛乌素沙漠北边缘，地理位置为东经109°29′，北纬39°03′。图克镇属温带大陆性气候，受蒙古高气压影响极大，西北冷空气控制时间长，年平均气温为6～8℃。具有干旱多风、气候干燥、温差变化大等特点。当地降水稀少，年平均降水量为375 mm；蒸发量大，年平均蒸发量为2 592 mm。

2.2 计算过程

数据来源于内蒙古鄂尔多斯乌审旗图克镇煤化工工业园区地下水水质监测报告。

依据步骤1及对地下水监测资料进行对比分析，最终确定6个水质指标（即总硬度、溶解性总固体、氯化物、硫酸盐、氟化物、铁）作为评价指标，构建评价指标X=（总硬度，溶解性总固体，氯化物，硫酸盐，氟化物，铁）。

上述评价指标均属越小水质越优型，按公式（1） 进行标准化计算。以总硬度为例，计算该评价指标对7#水井的相对隶属度，结果如下：

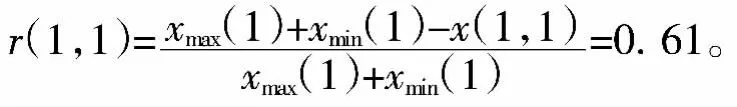
以此类推，计算出所有评价指标对井的相对隶属度值，并用隶属度值构建模糊评价矩阵R，计算结果列于表1中。

?

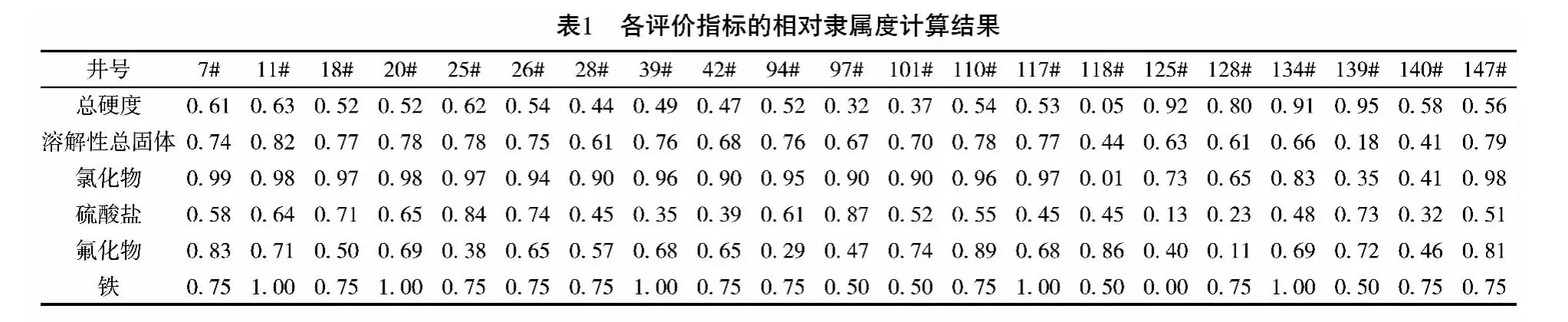
根据步骤3计算出样本标准差s（i）（i=1，2，…，6） 分别为0.202、0.153、0.254、0.187、0.195、0.230，相对重要性程度bm=2.0。通过公式（5），构建判断矩阵B如下：

针对步骤4，具体实现过程借助Matlab7.0软件进行编程，取各指标权重的变化区间为（0，1），参数d取为0.2［7］。借助遗传算法选择200次，加速10次，得到评价指标1～6的权重值分别为：0.160、0.110、0.237、0.142、0.151、0.200。与之对应的目标一致性系数CIC（n） =0.000 8<0.1，表明该判断矩阵具有满意一致性。而且指标3（氯化物）、指标6（铁） 和指标1（总硬度）所占的权重相对较大，与区域实际情况较为相符。

2.3 模糊综合评价结果

由计算出的权重指标，构建指标权重矩阵为A= （0.160，0.110，0.237，0.142，0.151，0.200）。根据步骤5，求得水质综合评价矩阵Z（j）= （0.771，0.821，0.724，0.800，0.741，0.745，0.651，0.742，0.667，0.672，0.633，0.635，0.762，0.766，0.353，0.469，0.548，0.787，0.567，0.500，0.754）。

根据最大隶属度原则，可见位于11#和20#处的地下水质为最优，位于118#和125#处的水质为最差。各水井地下水质的优劣情况见表2。

?

为了说明模型在地下水质评价中的可行性及精度要求，采用F值评分法对地下水质数据进行处理，处理结果见表3。

?

通过上述对比分析知，本方法的综合评价结果与F值评分法基本一致。但F值评分法所得的数据结果分层不明显，而本方法的数据结果分层明显，对管理者而言有利于做出最正确的决策。根据计算成果，需对上述水质较差的区域，采取地下水环境保护措施。

3 可视化计算成果

基于Arcgis具有强大的空间分析功能和显示功能［8］。利用Arcgis的专题图功能，采用按值渲染的方法，将本次综合评价结果以电子地图的形式显示出来，得到区域地下水质分类图，见图1。

4 结束语

1）利用模糊综合评价矩阵构建适用于确定指标权重的判断矩阵，并采用遗传算法对判断矩阵一致性进行检验、修正及确定权重的新模型，避免了因人而异产生的主观臆断性，并将该模型成功应用于地下水质评价中。

2）通过对乌审旗图克镇地下水监测资料进行实例分析表明，采用该方法计算出的水质优劣排序结果合理、客观，且操作简单、精度高，具有实际应用和推广价值。

3）本次评价指标是人为筛选之后确定的，在今后的评价中采用何种指标需进一步研究。

［1］许国志，顾基发，车宏安.系统科学［M］.上海：上海科技教育出版社，2000.

［2］金菊良，丁晶.水资源系统工程［M］.成都：四川科学技术出版社，2002.

［3］刘泽双，章丹，康英.基于遗传算法的模糊综合评价法在科技人才创新能力评价中的应用［J］.西安理工大学学报，2008（3）：376-381.

［4］陈守煜.复杂水资源系统优化模糊识别理论与应用［M］.吉林：吉林大学出版社，2002.

［5］汪应洛.系统工程［M］.2版.北京：机械工业出版社，2001.

［6］金菊良，魏一鸣，付强，等.计算层次分析法中排序权值的加速遗传算法［J］.系统工程理论与实践，2002，22（11）：39-43.

［7］金菊良，魏一鸣，丁晶.基于改进层次分析法的模糊综合评价模型［J］.水利学报，2004（3）：65-70.

［8］张成才，李红伟，吴瑞锋，等.基于GIS的水质模糊综合评价方法研究［J］.人民黄河，2009，31（5）：52-53.