内填部分混凝土钢桥墩延性性能简化计算方法

徐旻洋，高圣彬

(上海交通大学土木工程系，上海200240)

钢管混凝土结构具有承载力高、塑性和韧性好、耗能能力强等优点，已被广泛应用于土木工程领域［1－2］。在纯钢桥墩中内填部分混凝土，既可以提高其抵抗车辆撞击的能力，又可以提高其吸能能力并改善钢桥墩的延性［3］。在已有研究中，通过建立钢桥墩的三维有限元分析模型，基于不同的翼缘宽厚比、柱长细比和混凝土填充率这三个参数，对桥墩的滞回曲线、屈曲模态、延性系数、刚度退化以及耗能能力等进行分析比较。翼缘宽厚比对部分填充混凝土钢桥墩的承载力影响较小，但对达到极限承载力后的荷载下降段以及能量吸收能力的影响较大。随着翼缘宽厚比的增大，荷载下降的速度加快。柱长细比对部分填充混凝土钢桥墩的承载力影响较小，对累积吸能能力的影响较大。随着柱长细比的增大，累积吸能能力逐渐下降。混凝土填充率的变化将影响钢桥墩的屈曲模态，填充混凝土后的钢桥墩承载能力将大幅提高且有较好的防车辆撞击能力［4－5］。在已有的采用二维梁单元模型模拟箱形截面钢桥墩的延性研究中，一般假定底部混凝土以及内填混凝土上方钢板，任一处有效破坏长度范围内的平均压应变达到所对应的极限应变时，就认为桥墩破坏。基于这种假定方法所得到的钢桥墩延性偏大，且规律性较差［6］。本文从设计角度，使用二维梁单元模型预测钢桥墩的延性。将分析得到的桥墩延性与试验结果进行对比，验证了使用延性修正系数后的二维简化模拟分析方法进行设计的合理性和可行性，并提出了确定钢桥墩最优填充率的方法。

1 有限元建模

1.1 模型基本参数

根据试验试件［7］的几何参数、材料参数和加载条件，建立了二维梁单元分析模型(S73－32－30、S73－32 －50、S83 －32 －30、S83 －32 －50)。试件编号“S73－32－50”中，“73”表示翼缘宽厚比为0.73，“32”表示柱长细比为 0.324，“50”表示混凝土填充率为试件高度的0.5倍。以此4个试验模型为基础，基于翼缘宽厚比、柱长细比和混凝土填充率三个参数，建立其它16个二维梁单元模型以作对比分析。

1.2 模型建立

钢桥墩结构示意图如图1－(a)所示。图中的h代表桥墩高度，hc代表混凝土的填充高度。图1－(c)为钢桥墩横截面示意图。利用有限元分析软件DIANA建立钢桥墩二维梁单元模型，如图1－(b)所示。将有效破坏长度le(0.7b)区域均分为三个梁单元，在保证梁单元长度基本相同的前提下，将其余部分进行均分。此外，在填充混凝土区域，采用两种梁单元分别模拟钢箱形桥墩以及内填混凝土，且使这两种梁单元共用结点。

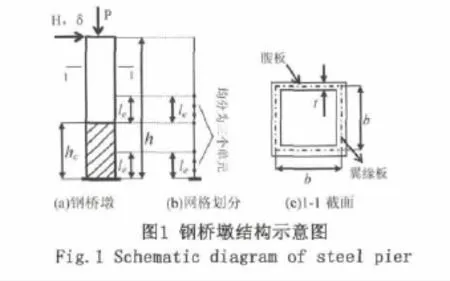
1.3 应力－应变关系

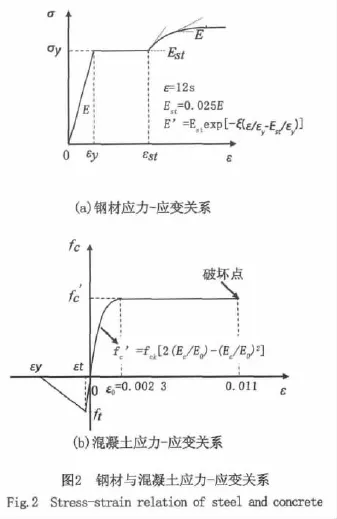
在有限元分析中，钢材采用具有屈服平台的应变强化型的应力 － 应变关系［8－9］，如图2－(a)所示。在具有屈服平台的应变强化型模型中，用一根曲线表示应变强化开始后的区域。取钢材屈服应力 σy为 261 MPa，弹性模量Es=2.09×105MPa，泊松比 υ =0.3。

混凝土单轴应力－应变关系如图2－(b)所示，其中混凝土抗压强度fc'=32 MPa，极限应变εcu=0.011，弹性模量Ec=3 ×104MPa，泊松比 υ =0.16，抗拉强度ft=2.63 MPa。混凝土受拉区采用线性软化模型，取钢板的屈服应变εy作为裂缝应力降为零时的应变。

1.4 加载方式

在试件顶部施加0.2Py(Py为钢桥墩轴向屈服压力)的恒定轴力后，在同一位置施加水平渐增位移至 10 δy。

柱顶水平屈服荷载Hy与水平屈服位移δy按公式(1)、(2)计算。

其中，W为钢箱形截面沿主轴的抗弯截面模量;I为截面主轴惯性矩。

1.5 钢板极限应变

对于承受恒定轴压与渐增弯曲荷载共同作用下的箱形截面构件段，其极限应变公式如下［8］:

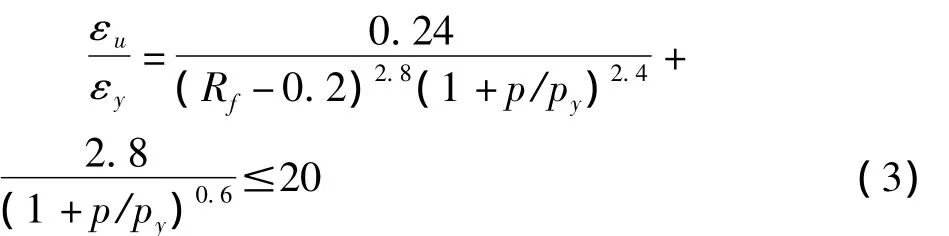
上式中，0.2≤Rf≤0.7;0.0≤p/pf≤1.0

1.6 试件的破坏准则

钢桥墩的破坏通常由钢板发生局部屈曲所致。局部屈曲发生在试件底部钢板或者内填混凝土上部钢板处(有效破坏长度范围内，le=0.7b)，这取决于混凝土的填充率。试件的破坏准则为底部混凝土以及内填混凝土上部钢板，任一处有效破坏长度范围内的平均压应变达到所对应的极限应变时，就认为桥墩破坏［6］。

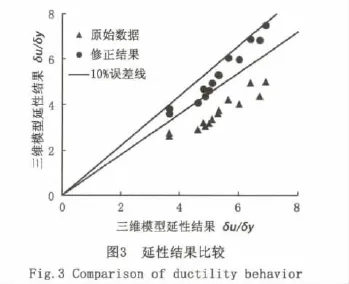
当局部屈曲发生在内填混凝土上部钢板时，由内填混凝土上部钢板在有效破坏长度范围内的平均压应变达到极限应变这一破坏准则，所确定的二维模型延性结果与三维精确有限元分析结果吻合较好。当局部屈曲发生在底部钢板时，由底部混凝土在有效破坏长度范围内的平均压应变达到极限应变这一破坏准则，所确定的二维模型延性结果偏大，且规律性不强。为此，对于局部屈曲发生在底部钢板的试件，本文提出新的破坏准则。选取底部钢板单元在有效破坏长度范围内的平均压应变代替相同位置的混凝土单元压应变，所得的延性结果整体偏小，如图3中的三角标记所示，这是由于内填混凝土对钢板发生屈曲变形有一定的约束作用，而现有的钢板极限应变破坏准则未考虑该作用。本文提出对底部钢板的极限应变进行修正的方法，将底部钢板的极限应变乘以修正系数α后得到的计算结果作为二维简化模型延性修正结果。

1.7 二维简化模型延性结果修正

在三维模型中，取试件达到最大荷载Hmax后，荷载下降至Hmax的0.95倍处所对应的位移为试件的极限位移δu，延性系数μ为δu/δy;在二维模型中，当底部钢板以及内填混凝土上方钢板两处有效破坏长度区域内，有一处出现ε/εu=1的情况，即可判断试件达到极限承载力，此时的位移称为试件的极限位移，其与试件水平屈服位移的比值即为构件的延性。

定义延性的误差为二维模型延性结果与三维模型延性结果的比值。定义总误差为各试件的延性误差与1的差值的平方和。通过数值拟合方式，确定最适合的修正系数α，使得总误差最小。如表2所示，修正系数α取为1.6时的总误差最小。图3示二维与三维模型延性结果的比较，可以看出修正后的延性误差较小，两者误差基本处于10%误差线内。

1.8计算结果与试验结果比较

图4示由二维梁单元模型得到的水平荷载－水平位移曲线与试验结果［7］的比较，其中Hy、δy分别为试件水平屈服荷载与水平屈服位移，可以看出:

(1)由二维梁单元模型得到的水平荷载－水平位移曲线与试验结果的滞回曲线骨架线相比，极限承载力和延性吻合较好，表明本文所建立的二维梁单元模型具有较高的精度。

表1试件底部钢板极限应变的修正系数αTab.2 Correction coefficient of failure strain of steel segment near pier base

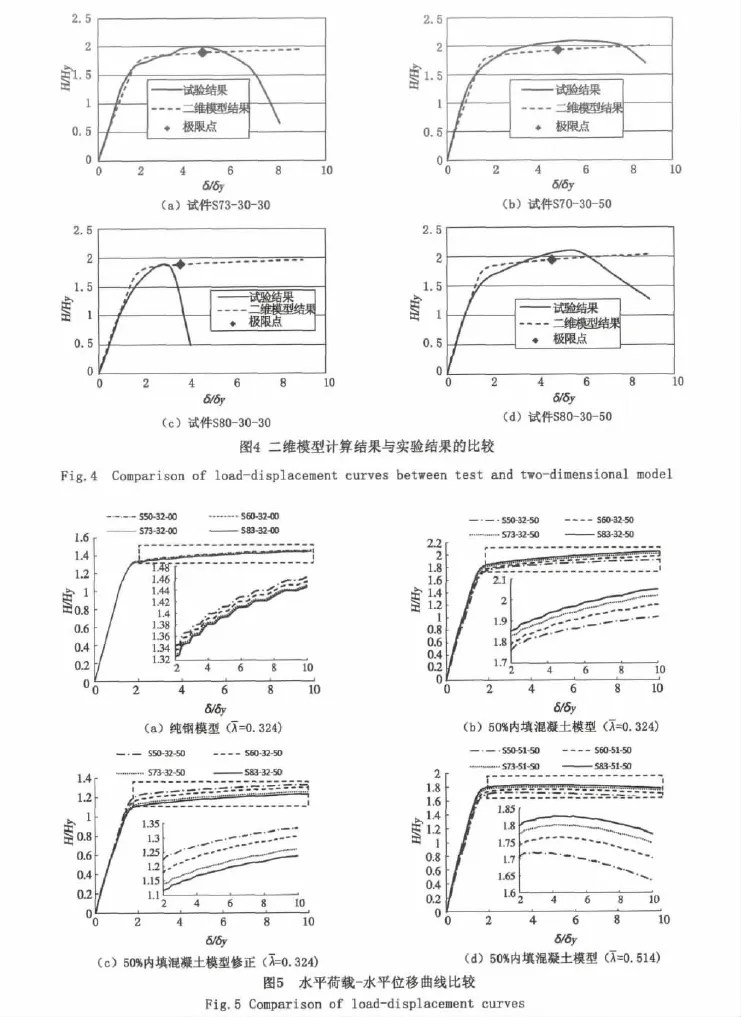
(2)对于两个30%填充混凝土模型，二维梁单元模型得到的试件延性与三维结果吻合较好。对于两个50%填充混凝土模型，二维梁单元模型得到的试件延性结果偏小，从设计角度来讲，是偏于安全的。

2 有限元分析结果

2.1 水平荷载－水平位移曲线

图5由二维梁单元模型所得水平荷载－水平位移曲线比较，可以看出:

(1)对于纯钢模型，如图5(a)，试件的承载能力随着翼缘宽厚比的减小而增大。对于内填混凝土模型，如图5(b)和5(d)，翼缘宽厚比较小的试件承载能力反而较低，与纯钢模型的结论相悖，这是由于在无量纲化的过程中，采用的水平屈服荷载Hy中没有计入混凝土的贡献。

(2)为了在无量纲化过程中考虑混凝土的贡献，图5(c)为采用二维模型计算中底部钢板达到屈服应变时对应的荷载“Hy计”进行无量纲化后得到的荷载－位移曲线，可以看出此时试件的承载能力随着翼缘宽厚比的减小而增大，与纯钢模型的趋势相同。

(3)由图5(a)和5(b)可以看出，随着内填混凝土的增加，试件的极限承载力增大。与纯钢模型相比，50%填充混凝土模型的极限承载能力大幅提高。

(4)由图5(b)和5(d)可以看出，柱长细比参数决定了试件的整体失稳。当柱长细比等于0.324时，试件未发生整体失稳，荷载－位移曲线始终处于上升状态，而当柱长细比增大至0.514时，试件发生整体失稳，荷载－位移曲线中出现了下降段。

2.2 延性系数

根据1.6节、1.7节所述的延性计算方法，以及钢板极限应变修正系数α，得到各试件的二维延性结果与破坏位置，如表2所示。表2中同时给出了三维有限元分析得到的延性结果。可以看出:

1)对于局部屈曲发生在内填混凝土上部钢板的试件，延性误差趋近于1，二维结果与三维结果吻合良好;对于50%内填混凝土试件，在引入修正系数α后，二维结果与三维结果吻合良好;对于纯钢试件，随着翼缘宽厚比的减小，延性误差逐渐变大，最大延性误差为 0.66，与已有研究结果相符［6］。

2)表格第六列示修正后的二维模型延性结果。混凝土填充率的提高，可以提升试件的延性;翼缘宽厚比和柱长细比的增大会降低试件的延性。

3)表格中数据误差在合理范围之内，二维延性结果趋势正确，表明本文所建立的二维梁单元分析模型可以有效预测钢桥墩的延性。

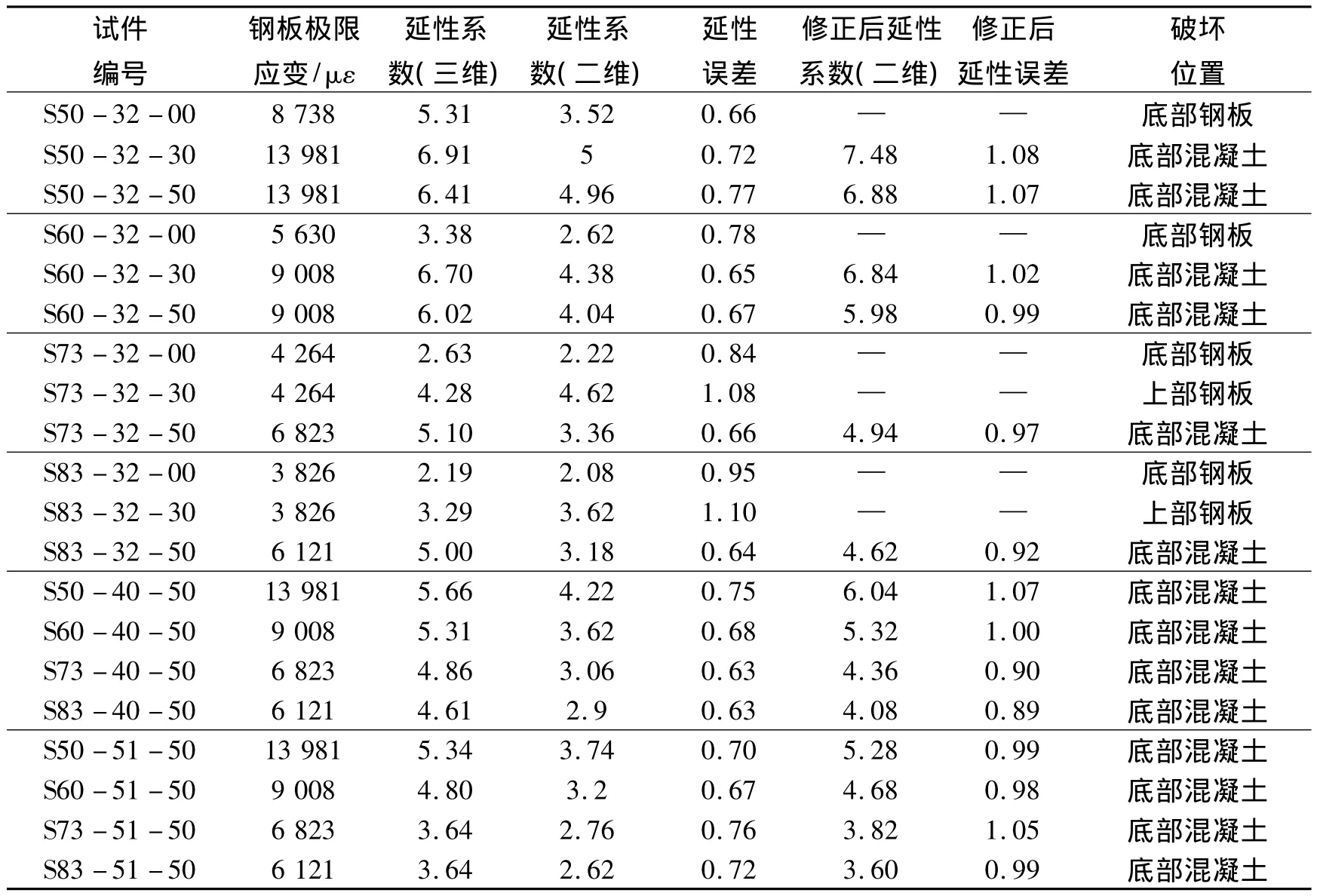
表2二维与三维延性结果比较Tab.2 Comparison of ductility behaviors between 2－D and 3－D models

3 钢桥墩最优混凝土填充率确定方法建议

对于部分填充混凝土钢桥墩，当桥墩底部混凝土和内填混凝土上方钢板在有效破坏长度区域内同时达到极限应变时所对应的混凝土填充率称之为最优混凝土填充率。

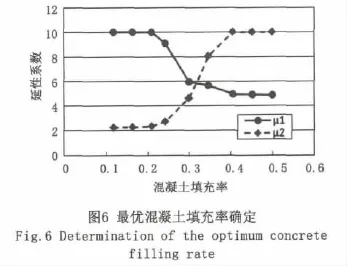
基于S73－32－00模型，设置混凝土初始填充高度为有效破坏长度，混凝土填充率的提升步为5%，建立各模型。基于如下两种算法确定延性系数:(1)由底部钢板在有效破坏长度范围内的平均压应变达到修正后的极限应变时所对应的延性系数μ1;(2)由内填混凝土上部钢板在有效破坏长度区域内的平均压应变达到极限应变时所对应的延性系数μ2。将各模型的μ1与μ2列出如图6所示，两者最为接近的混凝土填充率即为最优混凝土填充率。由图6可以看出翼缘宽厚比为0.73，柱长细比为0.324的模型，其最优混凝土填充率约为32%。

4 结论

1)对于局部屈曲发生在内填混凝土上部钢板的试件，二维模型延性结果和三维结果吻合较好。对于局部屈曲发生在底部钢板的试件，通过对计算结果的分析拟合，提出了钢板极限应变修正系数α(=1.6)。与三维结果相比，修正后的二维模型延性结果具有较高的精度。

2)混凝土填充率的提高，翼缘宽厚比和柱长细比的减小能够提高试件的延性。

3)提出了钢桥墩最优混凝土填充率确定方法建议，并应用于S73－32－00模型，发现该模型的最优混凝土填充率约为32%，为今后针对其它模型开展参数化分析确定钢桥墩最优混凝土填充率提供了理论依据。

［1］韩林海，杨有福.现代钢管混凝土结构技术［M］.北京:中国建筑工业出版社，2004.

［2］陈宝春.钢管混凝土拱桥设计与施工［M］.北京:人民交通出版社，2007.

［3］MATSUI C.Structural performance and design of concrete filled steel tubular structures［J］.JSSC Steel Construction Engineering，1994，1(2):11－24.

［4］GE HANBIN，USAMI TSUTOMU.Analytical study on ultimate strength and deformation of partially concretefilled steel beam－columns of box section［J］.Structural Engineering and Earthquake Engineering，JSCE，1995，513(31):77－88.

［5］王占飞，张海，张敏江，等.部分填充钢管混凝土桥墩抗震性能的数值分析［J］.沈阳建筑大学学报:自然科学版，2008，24(6):949－953.

［6］IRAJ H P，MAMAGHANI J A.Packer，Inelastic behavior of partially concrete－filled steel hollow sections［C］//4th Structural Specialty Conference of the Canadian Society for Civil Engineering，2002(6):5 －8.

［7］王跃东，高圣彬.内填部分混凝土箱形截面钢桥墩的滞回性能研究［J］.四川建筑科学研究院，2012，38(1):14－18.

［8］吉伯海，高圣彬.钢桥抗震与损伤控制设计指南:基础篇［M］.南京:河海大学出版社，2008.

［9］王占飞，隋伟宁，赵中华.基于性能的桥梁抗震设计理论与实践［M］.北京:中国水利水电出版社，2013.