群体智能的系统辨识

陈文雯,刘友宽,孙建平

(1.华北电力大学自动化系,河北 保定 071000;2.华北电力大学云南电网公司研究生工作站,昆明 650217; 3.云南电网公司电力研究院,昆明 650217)

群体智能的系统辨识

陈文雯1,2,刘友宽3,孙建平1

(1.华北电力大学自动化系,河北 保定 071000;2.华北电力大学云南电网公司研究生工作站,昆明 650217; 3.云南电网公司电力研究院,昆明 650217)

概括了系统辨识的方法,重点介绍了最小二乘法、群体智能算法中的粒子群算法和改进的粒子群算法,给出了估计模型的选择方法,并结合某1000MW火电机组实例,运用两种方法进行了系统辨识和仿真。仿真结果表明,最小二乘法可以完成对系统的辨识,但存在较大偏差;采用粒子群算法辨识结果良好。

系统辨识;最小二乘法;粒子群算法;仿真

1 前言

系统识别是建模的一种方法。建立数学模型有两种方法：解析法和系统辨识。

系统辨识的过程实质上就是函数拟合的过程,这里包括传递函数的结构和参数。因此,所要面临的是结构优化和参数优化的问题。如果已经对系统有了一定的了解,那么可以先给出系统模型描述函数的结构,然后辨识出函数中的参数即可,即把结构 (函数)优化问题转化成参数优化问题。

文中从传统系统辨识方法和群体智能系统辨识方法两方面入手,阐述系统辨识的方法,辨识实际工业控制系统,并对其进行仿真。

2 最小二乘法

最小二乘法 (LS)是估计理论的奠基石,其思想是使各次实际观测值和计算值之间差值的平方乘以度量其精确度的数值以后的和为最小。最小二乘法容易理解和掌握,利用其所拟定的识别算法在实施上比较简单。但由于最小二乘估计是非一致的、有偏差的,因而为了克服它的不足,形成了一些以最小二乘法为基础的辨识方法,如广义最小二乘法、辅助变量法和增广矩阵法,以及将一般的最小二乘法与其它方法相结合的方法,譬如最小二乘两步法和随机逼近算法[1]。

3 粒子群算法

3.1 PSO基本思想

PSO首先初始化一群随机粒子 (初始速度、位移及其决定的适应值都随机化),然后通过迭代搜索最优解。在每一次迭代中,粒子通过跟踪两个最优值来跟新自己,第一个就是粒子本身目前所找到的最优解Xbesti,即个体最优值。每个粒子都具有记忆功能,Xbesti是它们记住的各自曾经达到的最好位置。另一个最优值是整个种群目前找到的最优解Xbesti,即全局最优值 (假设群体之间存在着某种通信方式,每个粒子都能够记住目前为止整个群体的最好位置)。

下面以求某一函数Q(Xi)的极小值为例,介绍基本粒子群算法的实现方法[2]。

假设在一个N维的目标搜索空间中 (N相当于Q(Xi)中未知因子个数,也就是优化参数个数),有m个粒子组成的一个群体 (即m组可能解),其中第 i个粒子的位置表示为向量 Xi= (xi1,xi2,……,xiN);i=1,2,……,m其速度也是一个N维的向量,记为Vi=(vi1,vi2,……, viN)。随机产生一组 Xi,作为第一代初始种群,将Xi带入目标函数Q(Xi)就可以计算出其适应值,根据适应值的大小衡量Xi的优劣。对于最小化问题,目标函数值越小,对应的适应值越好。设粒子 i迄今为止经历的最有位置为 Xbesti= (xi1,xi2,……,xiN),相应的适应值记为Qbesti,则粒子的当前最好位置可表示为：

寻优过程中粒子群经历的最优位置记为 Xbestg= (xg1,xg2,…,xgN)其对应适应值即全局最优解为Qbestg。则粒子根据式(2)来更新自己的速度,即：

式 (2)中,i=1,2,…,m,n=1,2,…,N,t表示第t代。在速度更新时,不应该超出给定的速度范围,即要求Vi∈[-Vmax,Vmax],单步前进的最大值Vmax根据粒子的取值区间长度来确定。

然后按式 (3)来更新位置向量,即：

xin(t+1)=xin(t)+vin(t+1)(3)

式中的变量意义同前。根据实际问题来确定粒子的取值范围xin∈[xinmin,xinmax]。

这样一代一代地执行下去直到达到要求,取得极值。

对公式中一些符号意义作用的几点说明：①c1表示认知因子,c2表示社会因子。它们分别代表了向自身极值和全局极值推进的加速极值。实验结果表明,一般取c1=c2=2比较好,但实际上加速权值是可以变化的,而且如何变化将直接影响寻优过程;②r1,r2是0～1之间的随机变量。

PSO算法流程：

1)初始化,包括定义初始种群 (速度—位移模型以及种群大小等),进化代数,还有一些修正改进算法中可能用到的常量。

2)评价种群。计算初始种群各个粒子的适应度。

3)求出当前的Qbesti和Qbestg。

4)进行速度和位置更新。

5)评价种群。计算新种群中粒子的适应度。

6)比较Xbesti和Qbestg,若优越则替换。

7)判断算法结束条件 (包括精度要求和进化代数要求),满足则跳出循环,不满足则跳到 (4)继续执行。

以上为基本粒子群算法[3-5]。

3.2 粒子群算法的改进

为了改善基本PSO算法的收敛性能,本文提出了带权重的粒子群算法,即标准粒子群算法。这是对基本粒子群算法最早的一种改进。

标准 PSO主要是在式 (2)中引入了惯性权重ω,即：

惯性权重是为了平衡全局搜索和局部搜索而引入的,惯性权重代表了原来速度在下一次迭代中所占的比例,ω较大时,前一速度的影响较大,全局搜索能力比较强;ω较小时,前一速度的影响较小,局部搜索能力比较强。合适的ω值在搜索速度和搜索精度方面起着协调作用。因此,一般采用惯性权重递减策略,即在算法的初期取较大的惯性权值ω,使对整个问题空间进行有效的搜索,算法进行后期取较小惯性权值ω,以有利于算法的收敛。惯性权重递减公式为：

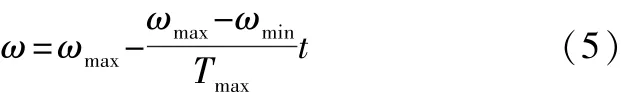
式中,ωmax和ωmin分别为ω的最大最小值,ω的取值范围在 [0,1.4]比较合适,但通常取在 [0.8, 1.2];Tmax、t分别是最大的迭代数和当前的迭代数。

另外,Clerc提出的收缩因子法也是一种标准的PSO算法。他是把基本的速度公式,即式 (2)改变为：

φ=c1+c2,φ＞4。通常情况下取 c1=c2=2.05,φ= 4.1,此时γ=0.7298。实验结果表明,两种方法差不多,收缩因子更有效率,但是在有些情况下无法得到全局极值点[6-9]。

4 算法的应用

4.1 估计模型的选择

确定模型的结构是决定模型质量关键性的一步[10-12]。

实际上,一个实际的物理表象,可以用无穷多的数学模型来描述,物理表象与数学模型不存在一一对应的关系,我们所能做的就是从各种数学模型中选择出一种来近似描述实际的物理表象。这一特性给选择模型结构带来困难。我们只好用对各过程领域的先验知识来假想一个模型结构。专家总结出的经验模型是：

式中：K为系统增益;子为纯迟延时间常数;T为系统惯性时间常数;β为微分时间常数;当系统为无自平衡时,有自平衡时;为惯性部分的阶次。

由式 (7)系统可以简化成以下几种模型结构。

1)高阶对象

绝大多数的热工对象有自平衡能力,并且属于多阶惯性环节。一般可以认为它是等容多阶对象,定义它为I型对象,即：

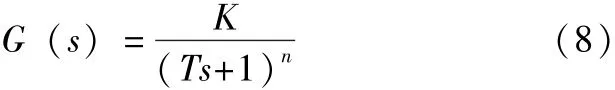
当求出的阶次n不是整数时,用近似的整数代替。

2)多容惯性对象

如果想描述有自平衡对象的细节,则可以用多容惯性对象,定义它为II型对象,即：

3)具有纯迟延的高阶惯性对象

当系统存在纯迟延时,可以加入纯迟延环节,定义它为III型对象,即：

当使用高阶对象时,可能会遇到困难,这时可以对其进行降阶处理。此外,纯迟延对象并不适合于系统分析,这时可以与高阶对象互换。如果不要求有特别高的精度,则可以用下面的方法进行升降系统阶次与纯迟延之间的关系相互转换来处理。

如果原传递函数如式 (10)所示,则可把它简化成：

两式中的参数关系为：

4)无自平衡能力对象

对于汽包水位系统等少数无自平衡能力对象,其传递函数可用式 (13)来描述,并定义它为IV型对象,即：

5)零稳态对象

对于具有微分作用的对象,当系统趋于稳态时,输出趋近于零,把这种对象定义为V型对象,即：

6)逆向响应系统

在工程中,存在一种逆向相应系统,它的表征是,在阶跃扰动作用下,系统的输出先朝着与最终趋向相反的方向变化,然后再朝着最终趋向变化。汽包锅炉的蒸汽量阶跃扰动引起的汽包水位变化就是逆向响应过程,在热工里被称为 “虚假水位”;循环流化床锅炉一次风阶跃扰动引起的床温变化也是一个典型的逆向响应过程。逆向响应系统的传递函数如式 (15)和式(16)所示,定义它为VI和VII型对象,即：

4.2 系统辨识与仿真

基于上述理论,用粒子群算法和最小二乘法辨识以下两个系统。

I.已知某火电机组在负荷下得到的蒸汽量变化对应汽包水位变化的传递函数为：(系统I)(17)

II.某1000MW超超临界火电机组,在负荷时,负荷发生变动后的各变量响应曲线如图1所示,从该图中截取的一段数据可用于系统辨识。辨识送风量和引风量变化引起炉膛压力变化的数学模型。(系统II)

图1 1000 MW机组负荷图

4.2.1 系统I辨识

系统I采用最小二乘法辨识的结果为：

V1=0.150 4,V2=4.945 0,V2=3.615 5,V4=3.685 4,V5=5.504 5。辨识后的传递函数为式(18)：

系统I采用粒子群法辨识的结果为：V1= 0.184 5,V2=8.971 6,V3=3.492 8,V4=2.830 3,V5=5.721 1。辨识后的传递函数为式 (19)：

最小二乘法辨识结果如图2所示。

图2 系统I最小二乘法辨识结果

把仿真步距设为500,在同一方波信号下观察比较最小二乘法和粒子群把对系统I的辨识结果。最小二乘辨识见图2,粒子群算法辨识见图3。

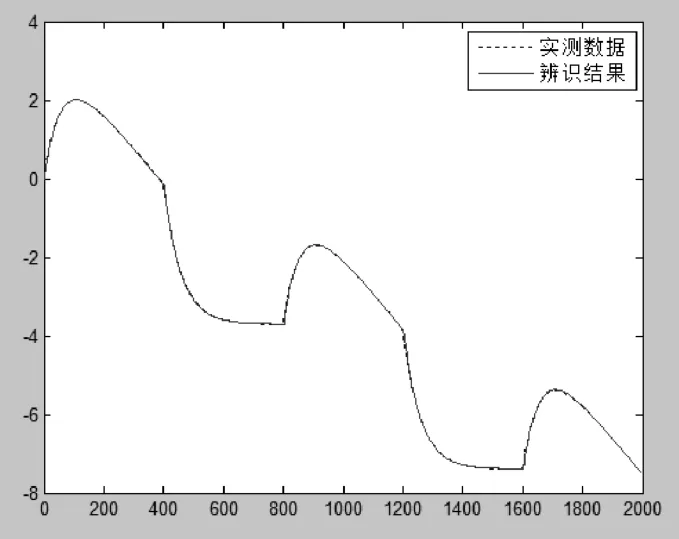
图3 同一方波信号下系统I粒子群辨识结果

比较图2、图3可知,采用最小二乘法辨识的辨识曲线大概能与实测数据拟合,但有明显误差。采用粒子群发进行系统辨识时,只要选择合适的参数,辨识曲线与实测数据的拟合效果很好,几乎完全重合。

4.2.2 系统II辨识

读取的现场数据见图4。系统辨识模型结构为：

图4 读取的现场数据

系统II采用粒子群算法辨识结果见图5。

图5 系统II粒子群算法辨识结果

辨识结果为：V1=0.577 3,V2=2.126 9,V3=1.859 5。近似为：

最小二乘法辨识。V1=0.524 3,V2=1.968 7,V3=2.2951,辨识结果见图6。

图6 系统II最小二乘法辨识结果

5 结束语

本文介绍了系统辨识的有关概念和方法,系统辨识实质上是结构优化和参数优化。重点介绍了粒子群算法和最小二乘法,并根据火电机组实例,应用这两种方法进行了系统辨识与仿真。

粒子群算法是一种全局随机优化算法,具有参数少、速度快的特点,从仿真结果可以看出粒子群优化算法辨识精度较好、速度快,且对输入输出观测量的要求可以根据实际情况方便选择。最小二乘法是传统的辨识方法,收敛速度较快,但存在局部最小问题,易出现产生非奇异矩阵导致收敛失败的情况。

[1] 王琳,马平.系统辨识方法综述 [J].电力情报,2001, (4)：63-66.

[2] 韩璞,等.智能控制理论及应用 [M].北京：中国电力出版社,2013.

[3] T.H.Kim,I.Maruta,T.Sugie.Robust PID controller tuning based on the constrained particle swarm optimization[J]. Automatica,2008,44(4)：1104-1110.

[4] 王俊伟,汪定伟.粒子群算法中惯性权重的调整策略[J].计算机工程,2007,33(11)：193-195.

[5] J.Chen,T.C.Huang.Applying neural networks to on-line updated PID controllers for nonlinear process control[J].Journal of Process Control,2004,14(2)：211-230.

[6] 何小贤,朱云龙,王玫.群体智能中的知识涌现与复杂适应性问题综述研究 [J].信息与控制,2005,34(5)： 560-566.

[7] 李凯.基于微粒群优化算法的结构系统识别 [D].同济大学土木工程学院,2008.

[8] J.Q.Han.From PID to active disturbance rejection control [J].IEEE Transactions on Industrial Electronics,2009,56(3)：900-906.

[9] V.A.Oliveira,L.V.Cossi,M.C.M.Teixeira,A.M.F.Silva. Synthesis of PID controllers for a class of time delay system [J].Automatica,2009,45(7)：1778-1782.

[10] 刘金琨,沈晓蓉,赵龙.系统辨识理论及MATLAB仿真[M].北京：电子工业出版社,2013.

[11] 田谦益.基于群体智能算法的非线性系统参数辨识[J].佳木斯大学学报 (自然科学版),2010,28(4)：502-505.

[12] 韩璞,朱希彦.自动控制系统数字仿真 [M].北京：中国电力出版社,1996.

System Identification Based on Swarm Intelligence

CHEN Wenwen1,2,LIU Youkuan3,SUN Jianping1
(1.Department of Automation,North China Electric Power University,Baoding,Hebei 071000; 2.North China Electric Power University Graduate Student Workstations of Yunnan Power Grid Corporation,Kunming 650217; 3.Smart Grid Department of Yunnan Electric Power Research Institute,Kunming 650217)

Establishment of the system model is necessary when it comes to study the control system.Therefore,system identification plays a crucial role in the study of control system,of which the essences are structural optimization and parameter optimization. The article summarizes the methods of system identification,focusing on the least squares method,the particle swarm optimization (PSO)which included in swarm intelligence algorithm and the improved particle swarm optimization,gives the selection method of estimation model and combine with a 1000MW thermal power instance,use two methods to identify and simulate the control system. Simulation results show that the least squares method of identification can be done on the system,but there is a big deviation and it can get good recognition results by using particle swarm optimization.

System Identification;Least Squares;PSO;Simulation

TP15;TP18

B

1006-7345(2014)03-0010-05

2014-05-06

陈文雯 (1989),女,硕士研究生,华北电力大学云南电网公司研究生工作站,从事控制理论与控制工程、新能源等领域研究 (email)961689821@qq.com。

刘友宽 (1973),男,云南电网公司电力研究院,长期从事水火电机组控制研究、新能源远程控制系统研究。

孙建平 (1961),男,教授,华北电力大学自动化系,长期从事控制理论与控制工程、模式识别领域的教学与研究。