基于MATLAB的磁悬浮系统控制器的设计与研究

叶云洋，蒋 燕，陈文明，罗小丽

（湖南电气职业技术学院，湘潭 411101）

基于MATLAB的磁悬浮系统控制器的设计与研究

叶云洋，蒋 燕，陈文明，罗小丽

（湖南电气职业技术学院，湘潭 411101）

针对磁悬浮系统的非线性、不稳定的性质，采用线性化处理方法建立了磁悬浮系统的数学模型，然后基于此模型设计了结构合理的PID控制器，并利用Matlab软件进行了仿真分析得到了合适的PID控制参数，最后验证了所设计的PID控制器的正确性和稳定性.

磁悬浮系统；MATLAB；PID控制器

0 引 言

磁悬浮系统（Magnetic system），是集合了电磁技术、控制技术和机械工程等于一体的高新技术产品，它利用了电磁场中的“同性相斥，异性相吸”原理使轴承中的转子悬浮起来工作，且转子的空间位置可以由先进的控制系统进行实时调节.它已经成为了当今高新技术领域的研究热点［1］.

1 磁悬浮系统的空间模型

如图1所示，磁悬浮控制系统主要由铁心、线圈、传感器、控制器、功率放大器及其控制对象刚体等元件组成系统采用位置传感器在线获取刚体位置信号，控制器对位移信号进行处理产生控制信号，功率放大器根据控制信号产生所需电流并送往电磁铁，电磁铁产生相应磁力克服重力使得刚体稳定在平衡点附近［2］.

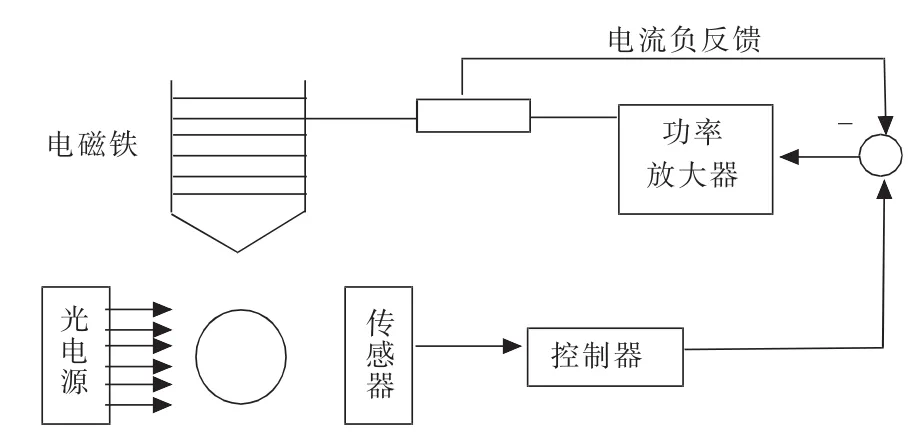
图1 磁悬浮系统结构图

控制对象是铁磁性材料做成的球体.设球的高度为h（t），线圈电流为i（t）.则磁悬浮动力学方程以及线圈回路电压方程分别为［3］：上式中，L为电磁铁线圈上的电感，R为电磁铁线圈，u（t）为系统的输入，h（t）为系统的输出.令加速度为零，得到维持刚体保持该位置的期望电流为：

上式中m为刚体的重量，g为重力加速度，k为球体和磁场间的耦合系数，为了建立适应的控制模型，需将非线性方程（2）为在平衡点附近线性化［4］，产生一组线性方程，为此引入状态变量：x1＝h，x2＝，x3＝i，则方程（2）变为：

将方程（3）在工作点x3＝i0，x1＝h0处通过泰勒级数展开进行线性化，得到系统的状态空间方程为：

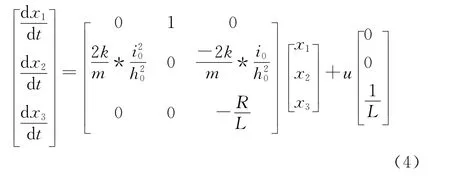
转化成传递函数形式：

2 PID控制器的设计

采用PID控制的的磁悬浮系统结构图如图2所示.

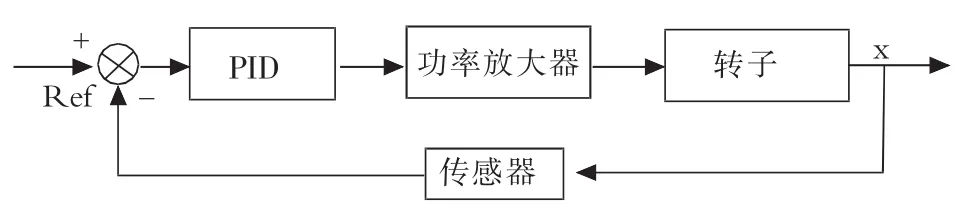
图2 磁悬浮系统的PID控制图

设PID控制器的传递函数为：

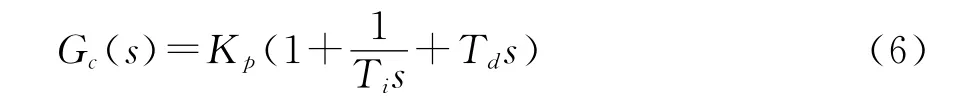
结合上一章得到的转子系统的传递函数（5），则得到系统的闭环传递函数为：

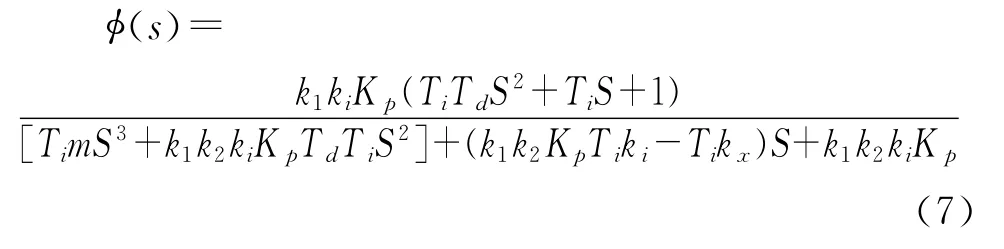
假设电路中的功率放大器的增益为B，传感器增益为A，则可以得到整个系统的传递函数为［5］：

根据以上分析，在MATLAB中构建PID控制系统仿真的模型如图3所示.

图3 PID控制器框图

3 磁悬浮系统的控制仿真

（1）为了使系统能够稳定运行起来，先将积分系数、微分系数TI、TD、KP置较小的值，若系统无法稳定运行，再考虑用其他的校正方式.

（2）再逐渐增大PID控制器的参数KP，直到系统出现等幅振荡，即临界振荡状态，记录此时临界振荡增益KC，临界振荡周期Tc，等幅振荡如图4所示.等幅振荡时：KC＝12.8，Tc＝25－10＝15.临界稳定法整定后参数：Kp＝7.6800；Ti＝7.5；Td＝2.

图4 统等幅振荡图

（3）再按照经验公式：Kp＝0.6 Kc，Ti＝0.5Tc，Td＝0.125 TC.整定相应的PID参数，然后利用MATLAB仿真采用PID控制器的磁悬浮模型闭环系统脉冲响应波形如图5所示.

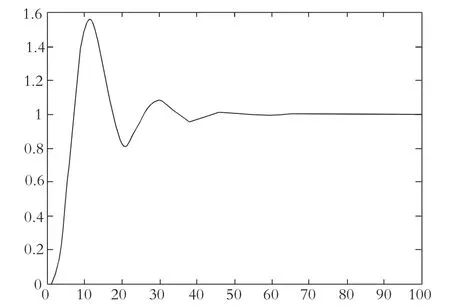
图5 磁悬浮模型闭环系统脉冲响应

从模拟磁悬浮脉冲干扰的结果可见，当磁悬浮模型受到干扰后会偏离平衡位置，当外界干扰消除后，系统在平衡位置振动上下几次，能够马上回到原来的位置，反映时间只有40ms，说明系统自动调节速度较快，且系统比较稳定［6］.

4 结 论

针对磁悬浮系统的结构特点，利用最基本的PID控制对其进行研究，研究表明：所设计的PD控制器结构简单，能对磁悬浮控制系统实现稳定的控制，同时系统动态性能良好.因此，对于一些固定的单自由度磁悬浮系统而言，PID控制是一种不错的控制方法，但是对于不确定因素太多的多自由度磁悬浮系统，需要进一步进行研究.

［1］胡业发，周祖德，江征风.磁力轴承的基础理论与应用［M］.机械工业出版社，2006，4.

［2］吕辉榜.基于MATLAB快速控制原型的磁悬浮控制系统研究［D］.武汉理工大学硕士学位论文，2008.

［3］Hartavi A E，Ustun O，Tuncay R N ，et al.The Design，Simulation and Experimental Study of Active magnetic Bearing［C］.Eleatric Machines and Drives Conference，IEEE Intemational，2001.

［4］唐 洁，李训铭.单自由度磁悬浮系统的状态反馈控制［J］.计算机测量与控制，2005，13.

［5］Zi－Jiang，Kouichi Miyazaki，Shunshoku Kanae，Kiyoshi Wada.Robust Position Control of a Magnetic Levitation System via Dynamic Surface Control Technique［J］.IEEE TRANSACTIONS ONINDUSTRIAL ELECTRONICS，2004，51（1）.

［6］刘克平，吴建军.H∞鲁棒模糊控制在磁悬浮球系统中的应用［J］.长春工业大学学报（自然科学报），2008，29（4）.

The Design and Research of Magnetic System Controller Based on MATLAB

YE Yun－yang，JIANG Yan，CHEN Wen－ming，LUO Xiao－li
（Hunan Electrical College of Technology，Xiangtan 411101，China）

Magnetic system is a complex，nonlinear and unstable system.Based on this property，the mathematical model of magnetic system is established by the linearization method.Based on this model，a PID controller is designed with reasonable structure，and the suitable PID parameters are obtained by using MATLAB software，Finally，the results show the correctness and stability of PID controller.

magnetic system；Matlab；PID controller

TP273

A

1671－119X（2014）02－0020－03

2014－03－05

叶云洋（1982－）男，硕士，讲师，研究方向：电力电子技术，自动控制技术.

book=181,ebook=181