一元线性回归算法在生物化学分析仪上的应用研究
沈增贵,邓红玉
一元线性回归算法在生物化学分析仪上的应用研究
沈增贵,邓红玉
目的:实现一种应用于生物化学分析仪的定量分析方法。方法:利用一元一次线性回归模型,结合标准曲线来计算待测样本的浓度值。结果:经过验证和临床测试,该算法可满足性能要求,且有效可行。结论:该方法能很好地满足临床应用,并能扩展到工业检测、食品安全等领域。
一元线性回归;生物化学分析仪;最小二乘法
0 引言
生物化学分析仪是目前常见的临床检验设备之一,在糖代谢检查、心脏疾病检查、肝功能检查、肾功能检查方面都起着重要作用。常见测试项目包括谷丙转氨酶(ALT/GPT)、谷草转氨酶(AST/GOT)、碱性磷酸酶(ALP)、总胆红素(T.BIL)、直接胆红素(D. BIL)、总蛋白(TP)、白蛋白(ALB)、尿素氮(BUN)、肌酐(Cre)、二氧化碳结合力(CO2)、尿酸(UA)、总胆固醇(CHO)、甘油三酯(TG)、高密度脂蛋白胆固醇(HDL-C)、低密度脂蛋白胆固醇(LDL-C)、葡萄糖(GLU),可为临床上对疾病的诊断、治疗和预后及健康状态提供信息依据[1-2]。
生物化学分析仪按照反应装置的结构,可以分为连续流动式、离心式、分立式与干片式4类,按照自动化程度可分为半自动型与全自动型。目前常用的是分立式半自动生化分析仪与全自动生化分析仪。计算方法一般都支持终端法、两点法与速率法。
在临床检验应用上,对于样本测试结果可分为定性测试与定量测试。常见的定性测试方法有cutoff算法。定性项目的结果为阴性、阳性或者可疑,未提供具体数量等更加详细的信息。临床上如果需要知道某种物质具体含量的测试项,例如甲胎蛋白,则需要使用定量测试方法。
常见的定量算法有单点回归、线性回归、折线回归、指数回归、幂回归等[3]。其中单点回归、线性回归、折线回归属于一元一次线性回归,而指数回归通过对吸光度与浓度取对数后,转化为一元一次回归,幂回归也可以通过求对数的方法转化为一元一次回归。因此,本文讨论的一元一次线性回归具有通用性。
1 测试原理
生物化学分析仪属于光学式分析仪器,它基于物质对光的选择性吸收,即分光光度法,其测量原理基于比尔—朗伯定律,数学表达式为:
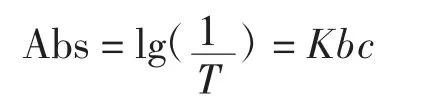
其中,Abs为吸光度;T为透光率,是透射光强度与入射光强度之比;K为摩尔吸收系数,它与吸收物质的性质及入射光的波长λ有关;b为吸收层厚度;c为吸光物质的浓度。
比尔—朗伯定律的物理意义是当一束平行单色光垂直通过某一均匀非散射的吸光物质时,其吸光度Abs与吸光物质的浓度c及吸收层厚度b成正比。
在生物化学分析仪上,单色器(滤光片或者光栅)将光源发出的复色光分成单色光,特定波长的单色光通过盛有样品溶液的比色池、光电转换器将透射光转换为电信号后送入信号处理系统进行分析。
2 标准液曲线的制作
在实际操作中,通过仪器只能获取到样本吸光度值。为了获取到样本的浓度值,需要增加几个对照物,也就是标准液。标准液的浓度是已知的,把标准液与样本一起测试,就能获取到二者的吸光度,再利用标准液的浓度值来估算出样本的浓度。
按照试剂说明书,配置好固定浓度的标准液后,在指定波长下测出它们的吸光度值,然后以吸光度为纵坐标,以浓度为横坐标,画出该溶液的标准曲线。根据标准曲线获取样本浓度的方法有3种。
2.1 标准比值法
即标准比较法。在相同的条件下,配制标准溶液和待测样品溶液的有色溶液,并测定它们的吸光度。由二者吸光度的比较,可以求出待测样品溶液的浓度。计算方法是:
待测样品溶液的浓度=待测样品溶液的吸光度/标准溶液的吸光度×标准溶液的浓度
2.2 标准系数法
即计算因数法。此法较为简单,将多次测定标准溶液的吸光度算出平均值后,按下式求出标准系数:
标准系数=标准液浓度/标准液吸光度
2.3 回归分析法
本文讨论的方法即是将制作标准曲线的各种标准溶液浓度的数值与其相应的吸光度值使用一元一次线性回归模型进行拟合,得到样本浓度值。
3 结果计算
3.1 数据预处理
通过测试,获取标准液的测试结果见表1。

表1 原始数据
为了验证该试剂测试结果是否具有线性,将上述的原始数据在直角坐标系上画散点图[4],如图1所示。

图1 标准液制作的散点图
从图1可以看出,试剂测试标准物所得的浓度与吸光度之间呈现某种线性关系,可以使用一元线性回归模型来估算样本的定量结果。
3.2 建立线性回归模型方程
对于所测得的原始数据,建立一元一次线性回归模型:

其中,y为浓度,x为吸光度,a、b为系数。
设在一次试验中,取得n对数据(xi,yi)(i=1,2,…,n),这n对数据(xi,yi)就是一组样本值,根据这一组样本值可以寻求一对系数a、b。但由于y是一个随机变量,所以通过另一组试验又可得到一对a、b的值[5]。也就是说,可以通过一组数据所得到的系数a、b的估计值,记作a^、b^,通过一组试验数据所求出的回归方程为:

对于每次试验取得n对数据(xi,yi),记yi是随机变量y对应于xi的试验值,记y^是试验值yi的回归值。每一个试验值yi与回归值y^i之间的差yi-y^i,可表示为2个纵坐标之差,这个差有正有负,其绝对值为。我们的目的是找到使所有这些距离之和为最小的一条直线,即最小。但由于绝对值在处理上比较麻烦,所以代之以平方和:



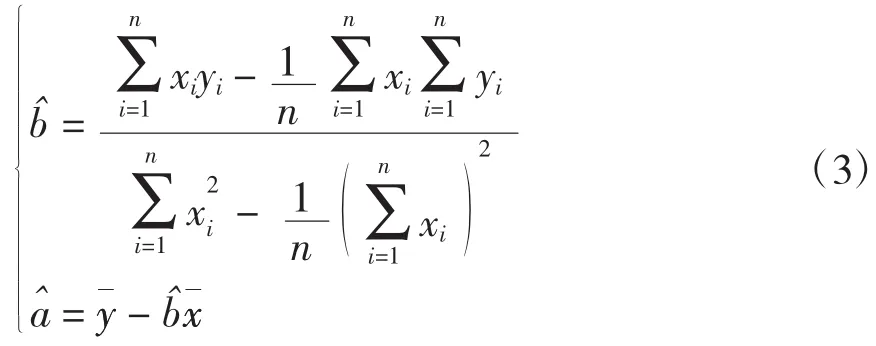
公式(3)或写成
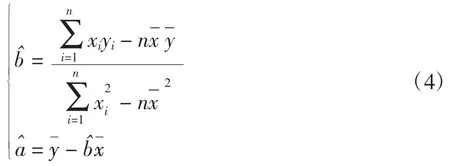
3.3 数据处理
根据上述算法,对测试数据进行预处理,结果见表2。
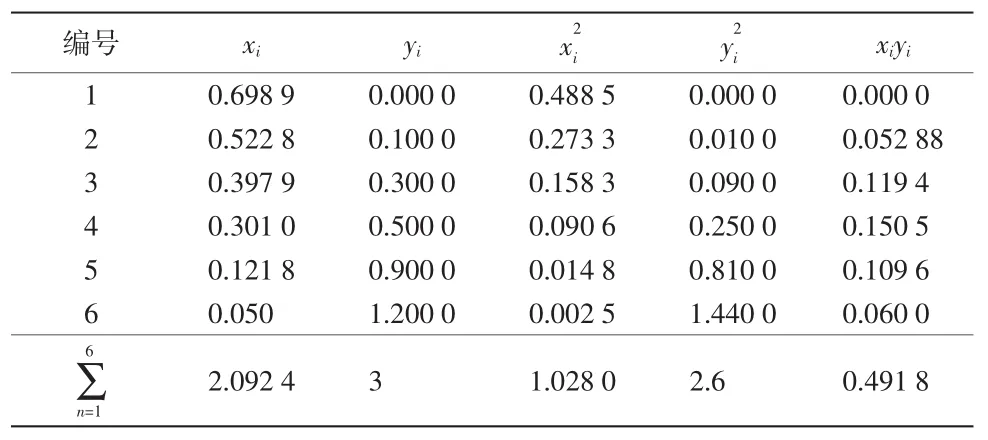
表2 原始数据预处理
拟合出的一元一次方程为:
y=1.139 7-1.834 6x
如果某个样本测试得到的吸光度为0.2A b s,则定量结果为:
1.139 7-0.2×1.834 6=0.772 9
4 效果验证
为了验证该算法的效果,我们使用生化常见的总蛋白(T P)与尿素2个项目,使用试剂标配的质控品对算法进行验证,验证项目是CV值。
4.1 试验原理
按照正常的生化项目测试步骤,设置该验证试验。测试方法为终点法,使用线性回归作为定量方式,测试对象为对应项目质控品[8]。在546 nm波长的光源下,使用比色法测试结果。加入试剂1、样本后测试,将原始数据记录下来,其中T P测试结果如图2所示。

图2 TP质控品测试结果二维图
图中实线为反应起始线与终止线,虚线为加入样本后的时间点。
使用仪器测试后,记录经过拟合计算出来的定量结果,记录为xi,用x表示平均值,n为测量的次数,通常为10次。S′为标准偏差。按照公式(5)、(6)计算CV值:
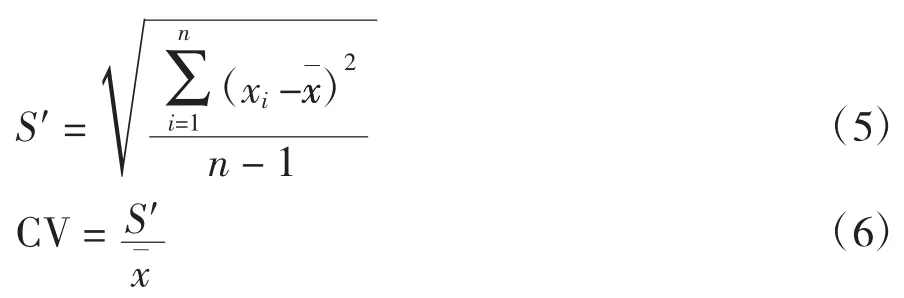
4.2 测试结果
按照上面描述的要求,测试T P项目与尿素项目,结果见表3。
根据质控品说明书,T P项目与尿素项目的CV值要求在2.5%之内。上述测试结果满足要求,该算法是有效可行的。

表3 TP项目与尿素项目CV值测试结果
5 结论
生物化学分析仪在临床检验、动植物疫病、食品安全方面有着广泛的应用。对于目前市场上常见的生物化学分析仪,本文给出一
(►►►►)(◄◄◄◄)种定量结果的计算方法,该方法经过CV值验证,并且结合临床试验,证明能满足使用要求。同时一元一次线性回归方法能扩展到幂回归、指数回归等其他算法,应用范围也可以延伸到工业物质检测、农药残留检测等方面,有着广泛的意义[9]。
[1]易龙强.基于一元线性回归理论的数字正弦信号频率测量算法[J].电测与仪表,2011,48(3):20-24.
[2]华德宏,刘刚.一种改进的一元线性回归算法[J].现代电子技术,2006,29(7):63-68.
[3]孟玲玲,孙常栋,韩宝如.基于最小二乘法和独立分量分析的间谐波检测算法[J].电力系统保护与控制,2012,40(11):76-81.
[4]赵郁森,陈晓亮.一元线性回归处理逆动态法实验数据[J].原子能科学技术,2009,43(7):586-589.
[5]汪宏良,陈丽峰,胡芳.生物化学分析仪检测结果的临床评价[J].检验医学与临床,2007,4(6):558-559.
[6]叶德谦,赵世磊.基于线性回归的关联规则相关性方法的研究[J].计算机研究与发展,2008,45(z1):291-294.
[7]鲁铁定,陶本藻,周世健.基于整体最小二乘法的线性回归建模和解法[J].武汉大学学报:信息科学版,2008,33(5):504-507.
[8]李克,叶英植.线性回归中粗差点判别法的改进及其应用[J].仪器仪表学报,2004,25(z1):723-724.
[9]陈清海,黎海文,吴一辉,等.生化分析仪的误差分析与建模[J].西安理工大学学报,2011,27(1):112-115.
(收稿:2013-09-10 修回:2014-02-25)
(栏目责任编校:李惠萍 孙丽丽)
App lication of Monadic Linear Regression Algorithm in Biochem istry Analyzer
SHEN Zeng-gui1,DENG Hong-yu2
(1.Departmentof Equipment,Nanfang Hospital,Southern Medical University,Guangzhou 510515,China;2.Department of Oncology and Hematopathy,the Third Affiliated Hospital of Southern Medical University,Guangzhou 510630,China)
To realize a quantitative analysis method used in biochemistry analyzer.By using the monadic linear regression model and standard curves,the concentration of the sample was calculated.Clinical trials proved that the method was feasible,and could meet the disired requirements.The method can be applied clinically,and can be popularized in the fields of industry,food safety and etc.[Chinese Medical Equipment Journal,2014,35(4):25-27,60]
monadic linear regression;biochemical analyzer;least squaremethod
R318.6;TH776
A
1003-8868(2014)04-0025-04
10.7687/J.ISSN1003-8868.2014.04.025
沈增贵(1982—),男,工程师,主要从事医疗器械维护保养以及质量控制等方面的研究工作,E-mail:287894309@qq.com。
510515广州,南方医科大学南方医院设备器材科(沈增贵);510630广州,南方医科大学第三附属医院肿瘤、血液科(邓红玉)

