含体积型缺陷管道强度的有限元数学模型研究

李 毅，詹燕民，向 安，李再春，刘 伟，陈雅楠，曹宏远

1.中海石油(中国)有限公司天津分公司，天津 300384

2.天津亿利科能源科技发展股份有限公司，天津 300384

含体积型缺陷管道强度的有限元数学模型研究

李 毅1，詹燕民1，向 安2，李再春2，刘 伟2，陈雅楠2，曹宏远2

1.中海石油(中国)有限公司天津分公司，天津 300384

2.天津亿利科能源科技发展股份有限公司，天津 300384

石油天然气管道普遍存在因腐蚀造成的体积型缺陷，而且随着服役时间的延长不断恶化，最终导致管道破坏失效。本研究以保障管道运行安全为目的，对含体积型缺陷管道剩余强度进行了研究。利用有限元软件分析了由于管道内部腐蚀缺陷引起的表面应力场，归纳了引起管道表面微应变变化的影响因素，利用软件拟合出相应的方程，建立了管壁应变与影响因素对应的三维模型，为进一步进行管道安全评估提供基础理论依据。

含体积缺陷管道；有限元分析；应力场；数学模型

0 引言

油气输送管道长时间服役后，会因外部干扰、腐蚀、管材和施工质量等因素影响而发生失效事故，导致泄漏、火灾、爆炸，造成重大经济损失、人员伤亡和环境污染[1]。在油气管道失效事故发生后，及时对失效模式、机理和原因进行分析和诊断，对于减少管道失效事故、防止类似事故的重演具有重要意义。失效分析和完整性管理是保障油气管道安全运行的重要手段[2]。

油气管道的腐蚀现象可以分为均匀腐蚀和局部腐蚀。实际上，完全的均匀腐蚀是不存在的，在油气管道腐蚀失效实例中局部腐蚀最多，其中包括点蚀、缝隙腐蚀、晶间腐蚀和应力腐蚀等。对于中低压的油气管道，其失效模式主要是点蚀[3]。经资料分析和微观观测，结果表明：微应变（应力）是失效过程的共性表现；且缺陷扩展始终伴随着表面微应变现象，临近失效阶段表面微应变明显增大。因此，可以通过管壁微应变来反映管道的腐蚀缺陷情况：当微应变达到设定的临界点时，说明缺陷可能造成管道失效，需要及时检修。

本文针对点蚀体积型缺陷进行分析研究，模拟管道体积型缺陷发展过程，建立仿真模型，施加边界条件及载荷。根据大量有限元计算分析和总结，归纳了引起管道表面微应变变化的影响因素，利用软件拟合出相应的方程，并建立符合管道强度影响因素的数学模型。

1 含体积型缺陷管道有限元模型

随着数值模拟技术的不断成熟，已经可以通过建立完整管道的有限元仿真模型来分析研究其受力状态，为研究腐蚀管道剩余强度提供了新的途径[4]。

1.1 建立模型

本文以龙口处理厂海底管道出地段为例选取模型，选用油气管道材质为 X60，管道规格为 D 356 mm × 12.7 mm。根据圣维南原理，为了消除边界效应，有限元模型的长度取管道直径的 3 ～ 5 倍，本文研究取管道长度为 1 000 mm。为了保持腐蚀坑底部剩余厚度的均一，圆柱型缺陷底部与管道本身保持相同的弧度。由于该模型体积很大，为了尽量减少单元和节点的数量，其几何模型周向取管道 1/4 周长，如图1所示。

图1 管道有限元模型示意

1.2 缺陷形状简化

现场管道表面的失效缺陷形式十分复杂，典型缺陷形貌的研究与确定直接影响着如何建立缺陷模型，并且对后续研究起着至关重要的作用。根据国标GB/T 18590-2001，典型缺陷的形状有图2（a）这几种[5]。最终根据体积型缺陷的常见类型简化为：圆柱型、V型、瓦罐型三种，简化如图2（b）所示。

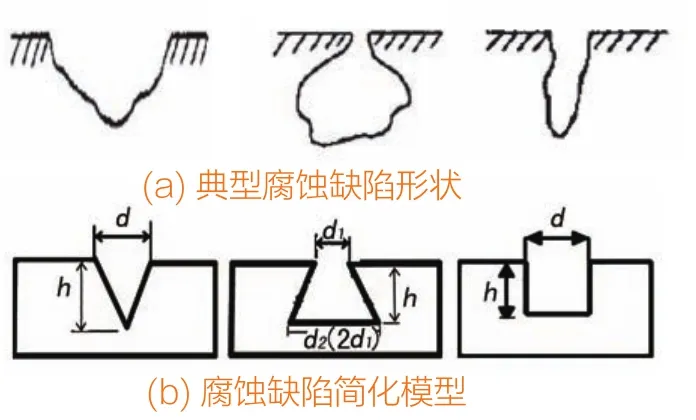
图2 典型腐蚀缺陷形状及简化模型

针对上述的分析结果，制订了如下的模拟分析方案：以研究单个典型缺陷模型为重点，分别研究不同直径、不同深度、不同压力下的圆柱型、V型、瓦罐型和球冠型等形状缺陷与管道表面应变之间的对应关系。

1.3 划分网格与边界条件[6]

本文研究选用 ANSYS 软件的三维10节点四面体SOLID 187单元进行自由网格划分。由于在腐蚀缺陷处应力和应变变化梯度大，所以对腐蚀缺陷部位和缺陷附近的网格进行加密，而在远离缺陷处网格较为稀疏。

缺陷形状规则且对称，模型中将纵向剖开的管壁截面上的垂直位移设为零。通常由于管道较长，而计算的腐蚀管道部分相对较短，因此可以不考虑管道轴向位移，两侧的垂直位移为零。管道的实际轴向约束情况理论上应该介于刚性约束与无约束之间。经计算比较，两种约束条件下缺陷应变极值变化趋势相同，仅仅是自由状态时缺陷应变极值变化曲线比轴向约束时整体偏高，说明用本方案的计算结果进行剩余强度评估更趋于安全和保守。由于实验过程中无法保证管道两端完全处于刚性约束状态，仿真模拟均采用不加轴向约束的方法以与系统的实验条件保持一致性。

油气管道在运营过程中，受到的载荷比较复杂，管道内压是主要的荷载，对于本文中研究的暴露在空气中的架空管道来说，仅对腐蚀管道内壁和缺陷表面施加均匀分布的载荷压力，大小取处理厂输气压力范围内的几个压力值，并进行求解计算，以便进行分析。

2 仿真实验

2.1 实验对象选取

本文中以架空管道作为实验对象，为了保证算法的安全性及统一性，首先对几种几何模型进行了归一化处理，选择将上述简化的那三种缺陷进行比较，计算结果如表1所示，在同尺寸下几种缺陷模型中，圆柱型缺陷的应变值总是大于其他两种缺陷，以该模型进行剩余强度的评价更加安全可靠，因此将圆柱型缺陷模型确定为评价的标准模型，算法研究也是基于此种模型。

表1 相同腐蚀深度相同直径不同形状缺陷应变值比较

2.2 实验方案设计

缺陷的尺寸范围定为 D2.0 ～ 14.0 mm，深度为 1/4～ 9/10 管道壁厚。计算条件为：管道尺寸D 356 mm × 12.7mm×1000mm；管道材质为X60；弹性模量为206 GPa；屈服强度450MPa；泊松比0.3。通过软件模拟计算研究深度和直径变化对外表面应变和应力的影响规律。

3 有限元计算结果分析

将这些缺陷模型计算结果进行参数化处理，找出它们产生的表面应变对应关系，拟合出数值关系方程。

根据材料的力学特性，管道失效是由于材料所受应力超过其屈服极限产生塑性形变而产生的，故在管道缺陷对管壁应变的影响范围内，主要关注其应力应变极值。管道的剩余强度可转换成应变，应变值便于测量，因此对于模型的计算结果也只分析管壁应变。根据不同直径、不同深度缺陷在不同压力下的计算结果寻找规律。

3.1 缺陷深度、直径对管道外壁应变的影响

在压力不变的情况下分别对不同直径和深度的缺陷模型进行分析计算。以 3.3 MPa 压力下计算结果为例，提取各个缺陷尺寸模型管壁周向应变结果数据极值，进行缺陷周向应变极值随缺陷直径和腐蚀深度变化的数据拟合，拟合曲线如图3所示。

图3 不同缺陷深度、直径对管壁应变影响拟合曲线

选用的拟合方程形式：Y=A+B×D；其中Y为管壁应变，D为缺陷直径。此五种深度方程对应的系数如表2所示。

表2 不同腐蚀深度拟合曲线方程系数A、B

取五种深度下方程系数A值与B值进行分析拟合，选取指数方程曲线如图4所示。方程类型为:。

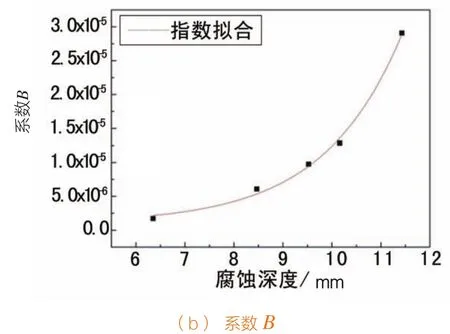
图4 系数A和B的指数拟合曲线

根据拟合结果得出系数A与系数B的表达式：

在材料弹性范围内，当缺陷直径不变时管壁应变与缺陷深度发展呈指数增长关系；当缺陷深度不变时管壁应变与缺陷直径发展呈线性增长关系。

3.2 管内压力对管道外壁应变的影响

绘制管道外壁应变随管内压力变化曲线，当缺陷直径和缺陷深度两者之一不变时，管壁应变随压力变化的线性拟合曲线几乎全部过坐标原点，即管壁应变随压力变化的线性拟合曲线近似呈正比例关系，因此给定一组缺陷直径D和缺陷深度h值时，圆柱型缺陷管壁应变与压力也近似呈正比例关系。

3.3 误差验证

该拟合方程表达式的计算结果与有限元计算结果的关系如图5所示。

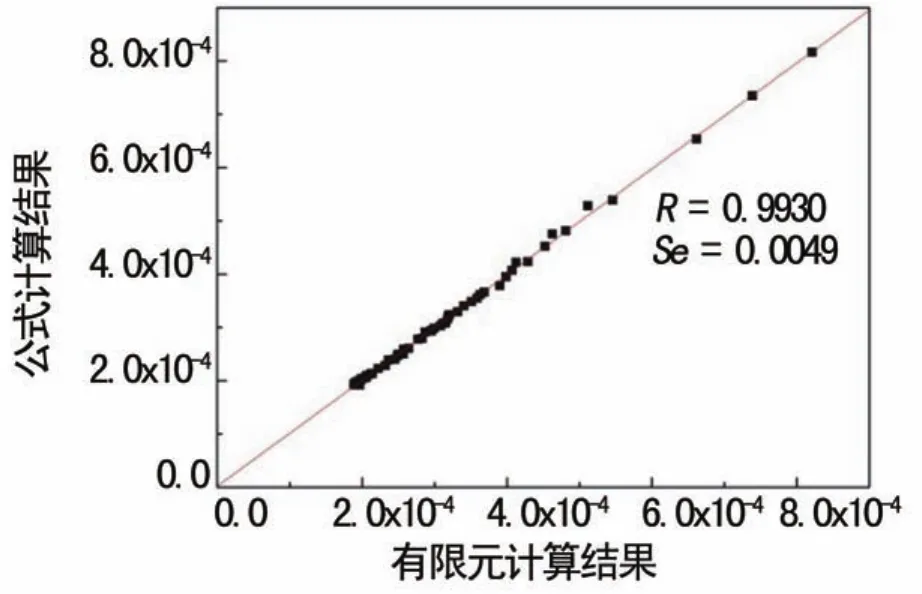
图5 有限元与方程的应力计算结果验证

该方程表达式对于预测腐蚀管道外表面的微应变具有较高的准确度，拟合结果线性系数（R）为 0.993 0，同一条件下两种结果的标准误差（Se）为 0.004 9，对所有数据点上得到的两种计算结果误差的统计发现，最大误差为 3.07%。

选取拟合算例以外缺陷尺寸进行有限元计算与公式计算的对比验证，如表2所示。

表2 误差验证

可见误差均在 5% 以内，能够满足使用公式计算圆柱型缺陷引起管道外壁应变代替有限元分析软件计算的要求。

3.4 数学模型

根据上述方程绘制出的在 3.3 MPa 工作压力下管壁应变随缺陷直径和缺陷深度变化的曲面，如图6（a）所示。图中的空心圆圈表示有限元计算的结果，所有有限元计算的这些数据点都分布在该曲面上。说明在本研究的范围内，该公式能很好地拟合这些离散的有限元计算结果。在压力改变时，曲面整体将上下平移形成平行曲面，如图6（b）所示。当压力连续时会形成一个上下底为曲面的柱体。

图6 管壁应变随缺陷直径和深度的变化曲面

4 结束语

本文介绍了一种腐蚀缺陷管道剩余强度分析的数学方法。利用有限元分析软件，建立模型仿真油气管道缺陷，进行油气管道体积型缺陷发展情况的腐蚀分析，通过所得到的管道缺陷应力场规律，总结出适用于该情况各影响因素(缺陷直径、缺陷深度、管道运行压力)的数学表达式，并建立起数学模型。该方法适用于暴露在空气环境下的架空管道，对于埋地和海底管道因受到不同的环境外载，还需进一步深化研究，以便该方法适用于各类管道。该方法可以在今后的管道评估中直接运用，既弥补了传统评价方法的偏保守又避免了建立复杂模型需花费的大量时间，并且计算精度达到了工程需要。

［1］卢禹赫.石油天然气管道运输安全问题的分析及探讨 [J].商品与质量·学术观察,2011，（5）：262-262.

［2］李鹤林，赵新伟，吉玲康.油气管道失效分析与完整性管理[J].理化检验—物理分册,2005,41（S）：24-31.

［3］颜 力，廖柯熹，蒙东英，等.基于点蚀缺陷分形特征的剩余强度评价[J].油气储运,2008,27（11）：43-45.

［4］骆华锋，白清东，王莉.基于有限元法在腐蚀管道剩余强度中的应用 [J].科学技术与工程,2008,8(23):6 335-6 338.

［5］GB/T 18590-2001,金属和合金的腐蚀点蚀评定方法 [S].

［6］李增亮，陈猛.外腐蚀管道剩余强度及剩余寿命的有限元分析 [J].润滑与密封,2010,35（10）：86-89.

Mathematical Model Based on Finite Element Analysis for Strength of Pipeline with Volumetric Type Flaws

Li Yi1,Zhan Yanmin1,Xiang An2,Li Zaichun2,Liu Wei2,Chen Yanan2,Cao Hongyuan2
1.CNOOC (CHINA) Limited-Tianjin,Tianjin 300384,China；
2.E-Tech Energy Technology Development Co.,Ltd.,Tianjin 300384,China

The volumetric type flaws caused by corrosion are ubiquitous in petroleum pipelines.With the extension of service time it will be worsening,and eventually leading to pipeline failure.In order to guarantee the pipeline safe operation,this research focuses on the influence factors of pipeline strength.Utilizing the finite element software to analyze the surface strain of the pipeline which has the internal volumetric type flaws,and the numerical equation is induced to reflect the factors which affect the pipe surface strain,and a three-dimensional mathematical model is established.This research provides theoretical basis of pipeline safety assessment.

pipeline with volumetric type flaw；finite element analysis；stress field；mathematical model

10.3969/j.issn.1001-2206.2014.01.001

李 毅（1975-），男，河北深州人，高级工程师，1997年毕业于中国石油大学（华东），现从事设备设施完整性管理工作，包括设备选型、运行维护、检测检验、风险评估等工作。

2013-03-15