我国工业用地招拍挂的竞价机制分析

◆刘 洋

我国工业用地招拍挂的竞价机制分析

◆刘 洋

文章使用拍卖模型分析了我国工业用地招拍挂竞价机制的问题，提出相应的解决方案。与此同时，文章使用全国333个地市层面2007-2011年的数据研究了土地招拍挂竞价机制形成的工业用地成交价格对经济增长、财政收入和房价影响，说明工业用地成交价格在经济社会中扮演的重要角色。基于研究结论，文章提出了相关的政策建议。

工业用地成交价格；经济增长；财政收入；房价

一、引言

我国的土地供给长期以来通过行政划拨，供经营实体无偿使用。这一制度虽然历经改革，但依旧充满了行政的色彩，土地的出让仍以划拨和协议为主，市场参与的成分很少，土地使用权的获得和成交价格主要通过行政指令确定。这样，地方官员可能会以开发、招商引资为名通过权力寻租而滋生腐败，而协议地价也普遍偏低，致使国有土地资产流失严重（王宏新和勇越，2012）。

针对以上这些情况，我国国土资源部于2002年颁布了《招标拍卖挂牌出让国有土地使用权规定》，规定我国经营性国有土地的使用权出让方式必须是招标、拍卖或挂牌之间的一种，这一制度简称为“土地招拍挂”。“土地招拍挂”主要是为了用地单位建立公平、公正、公开的土地使用权竞价出让环境、规范地方政府土地出让的行为并且优化城市的土地资源配置。从2007年开始，工业用地也进入了土地招拍挂的范围，我国土地招拍挂制度正式确立。

那么，现行的拍卖竞价机制是否真的起到了让市场充分反映土地价格的作用，拍卖制度形成的成交价格是否有效地解决了土地出让价格过低的问题，从而遏制了国有资产流失的现象？如果没有，是否有进一步改进的空间？

另外，招拍挂制度获得的土地收入已经在我国的经济社会中扮演了重要的角色。自1994年我国实行分税制改革以来，地方财政收入比重大幅下降，而支出比重几乎没有变化，地方政府的事权没有变化而财权的减小带来了两个问题。第一，地方政府财力的减小形成了地方经济建设的缺口。第二，地方政府需要履行提供公共品和公共服务的职责。因此地方政府急需借助土地出让来缓解财政压力，使得地方政府的融资和财政越来越依赖土地使用权出让获得的收入（陈超等，2011；王宏新和勇越，2012），土地出让金占地方政府财政收入的比重超过了60%（况伟大和李涛，2012）。与此同时，1998年底取消的福利分房制度将市场竞争机制引入了房地产行业，地方政府垄断了土地的所有权，房地产开发商通过“土地招拍挂”获得土地的使用权，因此房价也可能受到地价的影响。那么，工业用地使用权出让的成交价格对房价的上升起到了怎样的作用呢？

一支文献重点讨论了土地出让制度本身，李世蓉和马小刚（2009）使用全国2003-2006年和北京2005-2007年的数据，实证评估了土地招拍挂制度的绩效，发现土地出让市场中的一些问题，指出这一问题的来源是政府的干预。王宏新和勇越（2012）则说明，土地出让的初衷已经因为招拍挂制度的演进而逐渐被背离，成为地方政府获得短期经济利益的工具，从而提出国家应该加大财政转移支付力度，丰富和完善拍卖机制。然而，2011年5月11日，国土资源部发布的《关于坚持和完善土地招标拍卖挂牌出让制度的意见》声明要坚持和完善土地招拍挂出让制度，说明在相当一段长的时间内，这一制度本身将继续存在并且不断完善。况伟大和李涛（2012）也说明了这一制度的合理性，虽然地方政府的财政比较依赖于土地，但土地招拍挂制度在地方政府融资平台搭建的初期还是具有重大历史意义的，房价的高企并不完全是由这一制度带来的。然而，目前还没有文章重点研究土地招拍挂制度竞价机制的问题。既然地方政府现在还不得不倚仗土地出让金收入，那么地方政府真的通过设计拍卖机制实现利益最大化了吗？

另一支文献则研究了土地招拍挂制度的经济社会影响，重点在于对房价上涨的解释。王岳龙（2010）建立了一个斯塔克伯格博弈模型，说明短期内地价不会影响房价，而降低房价主要从开发商垄断入手，与陈超等（2011）的发现一致。王岳龙和张瑜（2010）使用中国省级面板数据发现土地招拍挂制度使得全国房价平均水平提高了13.2%，说明地价只会在更长的时期之内影响房价，而地价则是影响房价上涨的长期和短期原因，与黄静和王洪卫（2012）的结论类似。况伟大和李涛（2012）使用中国35个大中城市2003-2008年的土地市场和房地产市场的数据考察了土地出让方式与房价之间的关系，发现房价主要是供求决定的，而非由地价和出让方式决定。王岳龙（2012）使用干预分析模型和1999-2010年中国房价的月度数据说明土地招拍挂政策使得房价提高了4.7～15.7个百分点，但这一影响在不同地区有所差异。但是，这一支文献没有详实地记录地价与经济社会其他指标的联系，比如经济增长和财政收入，而仅仅局限于对地价和房价之间关系的讨论。

本文对我国现行的工业用地招拍挂的竞价机制进行了研究，重点考察招拍挂制度的绩效，政府是否从招拍挂制度中实现收益最大化；在现行的制度之上，提出新的拍卖制度；探讨工业用地成交价格对经济增长、财政收入和房价影响，说明工业用地成交价格在经济社会中扮演的重要角色。具体而言，我们使用拍卖模型对工业用地招拍挂的竞价机制进行建模，从理论上说明现行的一级密封价格拍卖诱使竞拍者故意低报自己的保留价格，这样可能会造成成交价格过低的问题。基于这一问题，我们提出使用二级密封价格拍卖的竞价机制，它会使竞拍者如实汇报自己的保留价格，这样达成的交易价格很可能会高于一级密封价格拍卖。但是我们发现，两种拍卖的竞价机制都存在缺陷，因而我们说明如何避免两种竞价机制的劣势、并且引入动态拍卖程序，从而获得更高的拍卖成交价格。接着，我们使用全国所有333个地市2007年至2011年的面板数据，实证分析了现行的拍卖竞价机制形成的工业用地成交价格对经济增长、财政收入和房价的影响，发现工业用地成交价格与三者呈正相关关系，这一效应在统计意义上和经济意义上都是显著的，并且这一相关性在考虑了地市差异、区域问题、价格的滞后效应以及内生性问题之后依旧稳健，说明工业用地成交价格在经济社会中扮演了重要角色。我们的研究结论对政策制定者有一定的启示作用。

本文接下来的部分安排如下。第二部分使用拍卖模型对现行的土地招拍挂的竞价机制进行建模，说明现行的竞价机制存在的问题并且提出新的竞价机制。第三部分利用全国所有333个地市2007-2011年的面板数据，实证分析竞价机制形成的工业用地成交价格在经济社会中扮演的重要角色。最后总结全文并且给出政策建议。

二、理论分析：拍卖模型

我国的工业用地的招拍挂制度，主要通过招标、拍卖或者挂牌的方式出售土地的使用权。无论采取何种模式，这种出售土地使用权的方式实际上是一个密封价格拍卖的机制（陈超等，2011；况伟大和李涛，2012；王宏新和勇越，2012），或者说是私有价值拍卖（Private Value Auction）：竞标者之间并不知道对方对于商品的估价，并且相互不会串通合谋以压低竞价，否则博弈的任何一方可以通过稍微抬高一点价格而获取所有的竞拍商品。

（一）现行的竞价方式

在我国，大多数的拍卖使用的是一级价格拍卖的方式，即竞拍者同时报价，以书面投标的方式竞买拍卖品，出价最高的竞拍者付出其出价水平获得拍卖品，与乔坤元（2012）中分析的股票IPO定价机制类似，工业用地使用权出让的竞拍方式也不例外。

我们假设竞拍者的估值独立同分布，其概率密度函数为f(v)，在支集（Support）[0,1]上严格为正。假设这里有N个竞标人，不失一般性我们令竞拍者估值的分布函数为F(v)，对于竞拍者i而言，给定其他人的竞价b(.)，也即b-i(.)=b(.)，竞拍者i的期望收益为：

最大化其期望收益，求解一阶条件得：

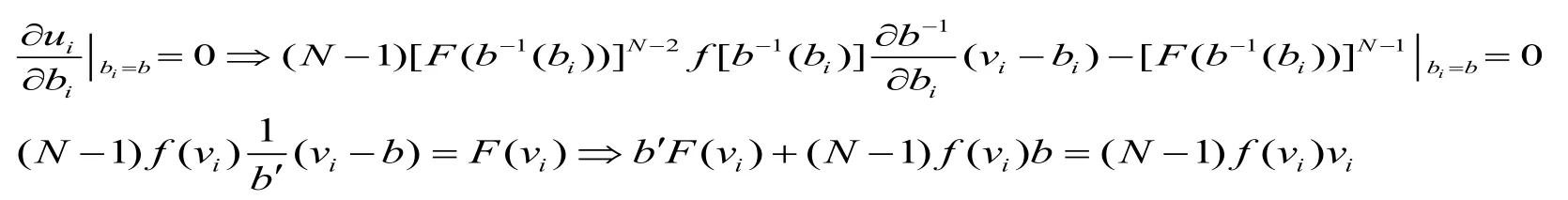
求解常微分方程，可得：

根据以往文献的做法，令常数项等于0，则有：

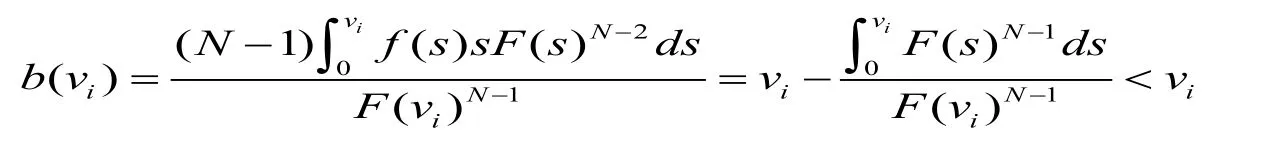
因此，均衡竞价策略是每一竞拍者竞价b(vi)以最大化自己的收益。

然而，可以看到，实际上在现行的一级密封价格拍卖的竞价机制下，竞拍者的竞价低于他们对于工业用地价值的真实评估vi。那么使用一级密封价格拍卖到底会使竞拍者低报多少呢？假设每一个竞拍者使用线性策略，即竞价为si=αvi+βi，由对称性可得竞拍者i的期望收益为：

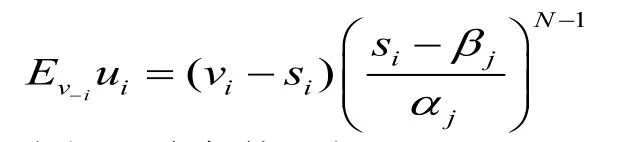
求解一阶条件可得：可见，如果竞拍者使用线性竞价策略，那么竞价较低，比竞拍者真实的估价低了1/N。

（二）二级密封价格拍卖

与一级密封价格拍卖的方式类似，二级密封价格拍卖同样要求竞拍者同时独立出价，竞拍物依旧由出价最高的竞拍者获得，但与一级密封价格拍卖不同的是，二级密封价格拍卖的成交价格是所有投标者的第二高价，即仅次于中标者的最高价格。

假设竞拍者i的竞价最高，令vm为其他人的最高竞价，Fm是其他所有人的竞价都低于竞价者i的概率，也即：

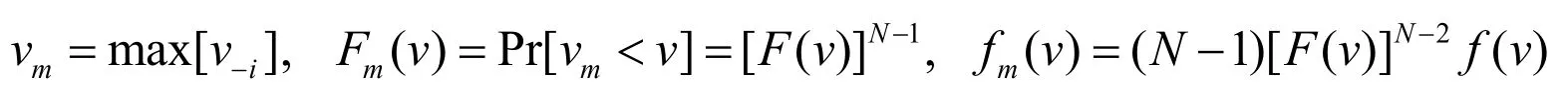
对于竞拍者i而言，给定其他人的竞价b(.)，竞拍者i的期望收益为：

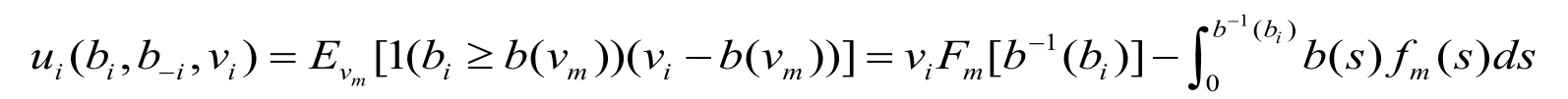
对于一个对称的纳什均衡：

求解一阶条件可得：

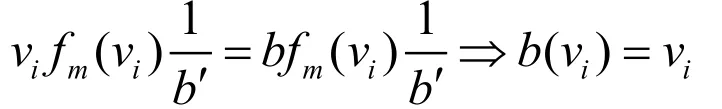
可以看到，如果采取二级密封价格拍卖，那么每一个竞拍者会报自己真实的估价。

（三）讨论

关于拍卖的经验文献证明，如果出价最高的两位竞价者的价差不是足够大（如第二高价低于最高价的50%），那么二级密封价格拍卖的成交价格要高于一级密封价格拍卖（McAfee和McMillan，1987）。这说明现行的竞价机制可能压低了工业用地的交易单价，更重要的是，如果不进行改革，可能会对经济社会带来负面影响。

当然，这两个拍卖制度都有一定的缺陷：现行的一级密封价格拍卖会让竞拍者低报自己对工业用地的估值，而二级密封价格拍卖方式的问题在于报价最高者按照第二高价进行交易。因此，设计该制度需要竞拍者如实汇报自己的估值，并且最高者需要付出非常接近自己报价的水平以获得工业用地的使用权。

一个可行的方案是，采取一级和二级密封价格拍卖相结合的方式，成交价格定在最高价和第二高价之间的某一个数值，对最高和次高价各取一个权重。按照二级密封价格拍卖的思路，可以证明各竞拍者会如实汇报自己的估值，并且最终的成交价格可以最大限度接近最高报价。

另外，按照二级密封价格拍卖的原理，可以考虑动态的公开叫价拍卖机制，依然以第二高价做成交价格。考虑竞拍者i，如果其他竞价者的报价没有超过自己的估值，那么竞拍者i还可能会报告一个远超过自己估值的报价以确保自己可以得到竞拍的工业用地使用权。如果有其他竞拍者的保留价值高于竞拍者i的报价，该竞拍者同样会报一个更高的报价。按照这样的逻辑，各竞拍者向上竞争（Race to the Top），这样最终的价格可能在估值最高者报价下方波动，也即成交价格p=vmax-ε，对于任意小的ε。因此，使用“二级公开叫价拍卖”的竞价方式会带来更高的工业用地成交价格。而对于“一级公开叫价拍卖”，按照之前的分析，竞拍者依旧会低报自己的估价，从而不能使拍卖成交价格最大化。

三、实证分析：现行工业用地竞价机制对经济社会的影响

本部分考察在现行的竞价制度下，形成的工业用地成交价格（以下均称为“工业用地成交价格”）与经济增长、财政收入和房价之间的关系，说明竞价机制及其形成的工业用地成交价格在我国经济社会中扮演的重要角色。

（一）数据和回归模型

我们使用地市（包括地级市、自治州、地区和盟）的数据进行考察。工业用地的平均交易价格来自于中国土地市场网，该网站记录了全国各个地市（包括地市所辖的所有市区和县）的每一块工业用地的交易情况。通过网页抓取，将地市所辖的市区和县的地价进行加权平均计算得到工业用地的平均交易价格。《中国区域统计年鉴》提供了全国各个地市详尽的经济数据，包括各个地市的经济发展状况、地方政府财政收支以及房地产市场情况。

囿于数据的可得性，我们使用全国333个地市2007年至2011年的数据进行考察。表1给出了各个变量的描述性统计量。由于地市的经济、财政以及房价的增长率存在一小部分的异常值，为了不使我们的结果受到异常值驱动（Outliers Driven），对经济增长率、财政收入增长率以及房价增长率进行了缩尾调整（Winsorize），将最极端的数值附上1%和99%分位数的数值。是否使用缩尾调整以及缩尾调整的分位数选择并不过分影响实证结果，其结论是稳健的。

可以看到在2007-2011年间，地市平均的GDP增长率为13.866%，最高的1%可以达到24.2%，说明我国的经济保持着较高的增速。地市的财政收入增长率平均值为26.181%，同样保持着较快的增长速度。与此同时，地市平均房价增长率达到了19.123%，增长最快的1%房价翻番。我国的经济构成中第二产业比重较高，平均值为48.275%，最高的达到了84.386%。

表 1 描述性统计量

我们考察竞价机制形成的工业用地成交价格带来的经济社会影响，使用各地市的GDP、财政收入以及房价的增长率做因变量，工业用地成交价格作核心自变量构建多元回归模型进行研究。

回归模型如下：

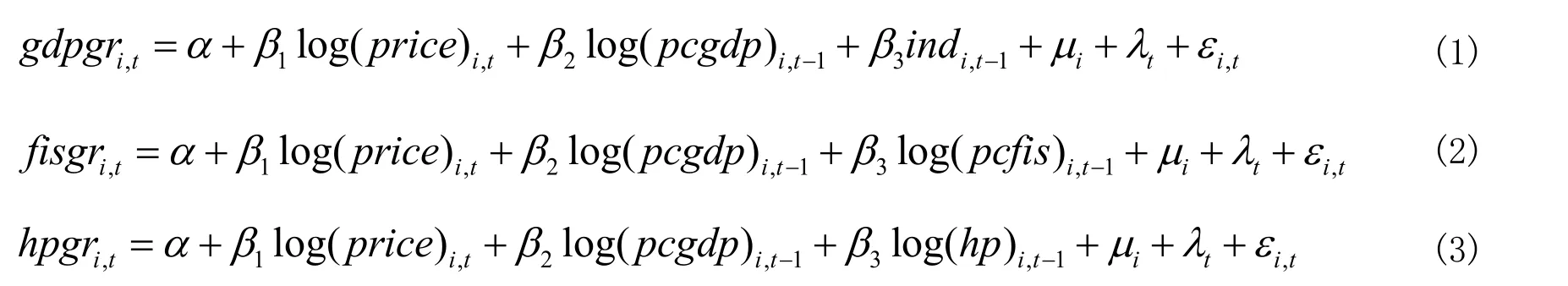
由于本文的数据是一个面板数据，所以用下标i代表地市，t代表时间。

其中，因变量分别为地市i在年份t的GDP增长率（gdpgri,t）、财政收入增长率（fisgri,t）以及房价增长率（hpgri,t），各变量经过CPI平减。

我们主要关心工业用地交易价格对数（log(price)i,t）对这三个因变量的影响，并且控制文献中常用的地市经济财政的控制变量，包括上一期的人均GDP对数（log(pcgdp)i,t-1）、上一期第二产业比重（indi,t-1）、上一期人均财政收入对数（log(pcfis)i,t-1）以及上一期房价对数（log(price)i,t-1）。控制变量都滞后了一期，因为经过一定的时间它们才会对经济增长、财政收入和房价产生影响。另外，同时考虑到地市不随时间变化、不可观测的因素带来的影响，使用μi来刻画地市固定效应，比如各个地市的文化和自然资源禀赋，它们会影响地市的经济财政情况，并且可能与工业用地成交价格有关，因此需要控制这一效应，否则回归结果会受到遗漏变量（Omitted Variable）的影响。同时控制时间固定效应λt，这一效应不随个体变化而变化，刻画了时间上的共同的冲击（Common Shock），比如2008年金融危机以及后续的四万亿刺激方案。

我们主要使用面板数据固定效应模型进行回归，如前所述，使用固定效应模型估计参数可以得到稳健、可信的结果。但是，固定效应模型的估计结果并不是最有效的，因此我们依旧对这一个面板数据使用混同横截面回归和随机效应回归模型进行估计，将得到的估计结果与固定效应模型进行比较，从而在保证一致性的前提下选取最有效的结果。我们重点关注参数β1，该参数刻画了经济增长率、财政收入增长率以及房价增长率对土地出让金价格的弹性。

（二）基准结果

对于这个面板数据使用三种估计方法：混同横截面模型、随机效应模型和固定效应模型，估计结果的稳健性逐步上升，但是估计效率逐渐下降，我们使用Breusch-Pagan检验（以下简称BP-LM检验）和Hausman检验来比较混同横截面模型和随机效应模型以及随机效应模型和固定效应模型的估计结果。

我们首先考察工业用地成交价格与GDP增长率之间的关系，结果汇报于表2。在没有其他控制变量的情况下，表2中第(2)列BP-LM检验拒绝了原假设，因此地市的个体效应是存在的，使用混同横截面模型会使得估计结果存在较大的偏差，第(3)列告诉我们固定效应和随机效应模型得到的结果都是一致的，但是随机效应模型更加有效。控制了上一期的人均GDP对数和第二产业比重之后，检验的结果发生了变化：从表2中第(5)列的BP-LM检验和第(6)列的Hausman检验可以看到，无论使用混同横截面还是随机效应模型，都不能得到一致的结果，因此只能使用固定效应模型进行估计，重点关注表1的第(6)列。

工业用地使用权出让的成交价格每上升1个百分点，那么地市的GDP增长率相应会提高0.358个百分点，估计系数在1%水平下显著。与GDP增长率的均值13.866%相比较，这一影响在经济意义上也是显著的，这说明工业用地招拍挂竞价机制形成的成交价格在经济增长过程中扮演着重要的角色，成交价格越高，经济的增速越快。在控制变量方面，上一年人均GDP对数正向显著影响GDP增长率，说明我国各地市的贫富差距有所拉大，人均GDP越高的地市经济增速越快。上一年第二产业比重对GDP增长率的影响不显著，但依然需要控制这一关键的因素，它与土地出让价格关系密切，而且会影响GDP增长率。

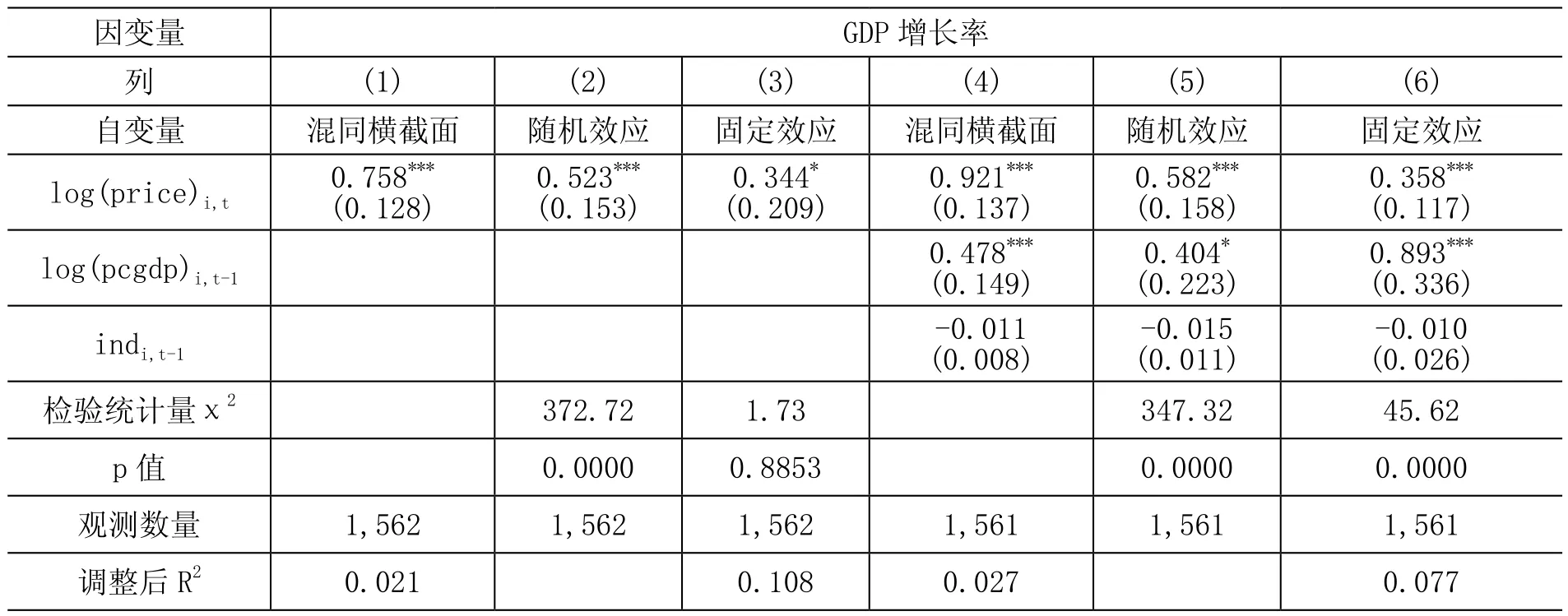
表2 基准回归结果1：GDP增长率

(2)***，**，*分别表示在1%，5%和10%水平上显著。下同。表3给出了工业用地成交价格对地市财政收入增长率影响的估计结果，与表2类似，没有控制变量的时候使用随机效应模型可以得到最佳估计，而使用控制变量后仅有固定效应模型能给出无偏一致的估计。我们关注表3的第(6)列：竞价机制形成的土地使用权出让价格每上升1个百分点，地市财政收入增长率提高1.123个百分点，估计系数在1%水平下显著，并且在经济意义上也是比较可观的。上一年人均GDP对数正向显著影响财政收入的增长率，估计系数在1%水平下显著，说明经济情况越好，财政收入增长越快。人均财政收入越高的地市财政收入增长越慢，估计系数同样在1%水平下显著，说明全国各地市的财政收入出现了一定的收敛的现象，上一期人均财政收入更多的地市下一期的财政收入增长率越低。

表3 基准回归结果2：财政收入增长率

表4给出了工业用地成交价格对房价增长率的影响。工业用地成交价格的上涨可能会带动居住用地的价格上升。根据BP-LM检验和Hausman检验的结果，我们依旧应该使用固定效应模型以获得稳健的估计，第(6)列给出了结果。可以看到，工业用地成交价格与房价增长率密切正相关，工业用地成交价格每上升1个百分点，房价增长率会上涨7.721个百分点，估计系数在统计意义和经济意义上都是非常显著的，这说明地价可能是引起房价上涨的一个不可忽视的因素，房价的上升很大程度上是成本拉动的。经济状况与房价增长率正相关，而房价在各地市之间也出现了收敛的现象，上一年房价越高，当年房价的增长率越低，上一年房价的估计系数在1%水平下显著。

表4 基准回归结果3：房价增长率

从表2、表3、表4的估计结果中，我们可以看到，招拍挂竞价机制形成的工业用地成交价格牵动着整个经济社会，更高的成交价格会助推经济增长，丰富地方财政，但同时也会加速房价的上涨。

（三）稳健性检验

我们得到的估计结果可能受到以下因素影响而并不准确，即工业用地成交价格与经济增长率、财政收入增长率以及房价增长率之间的相关性可能是不准确的。第一，人们可能会质疑城市的类别和所在区域。我国有四种地级行政单位，包括地级市、自治州、地区和盟。地级市作为主体存在，自治州属于民族自治区域，其经济财政情况可能会与地级市不同，而地区和盟则不属于一级政府，是省/自治区政府的派出机构，因此经济财政的状况也可能与地级市有所差异。我们需要分别对地级市和其他非地级市的样本进行回归考察。与此同时，根据以往文献，东、中、西部的发展模式存在一定的差异，因此工业用地成交价格的经济社会影响也会存在不同（王岳龙和张瑜，2010；王岳龙，2012；朱国忠等，2014），因此我们按照朱国忠等（2014）的划分方法，将各省、自治区划分为东、中、西部进行考察。第二，工业用地的价格可能并不能迅速反映到经济增长和财政收入上面，可能存在滞后效应，因此我们使用工业用地成交价格的滞后项作自变量进行考察。第三，经济增长、财政收入和房价也有可能会反向影响工业用地的价格（王岳龙和张瑜，2010；黄静和王洪卫，2012），内生性（Endogeneity）是我们需要考虑的，否则得到的工业用地成交价格与经济增长、财政收入和房价之间的相关性可能是有偏不一致的，我们使用工具变量法（Instrumental Variable，IV）和广义矩估计（Generalized Method of Moment，GMM）进行克服。

1.子样本检验

(1)城市的类别

我们首先按照城市的类别对样本进行划分，分为非地级市和地级市两个子样本。表5汇报了相关的结果。前两列汇报了GDP增长率与工业用地成交价格之间的相关性，可以看到无论是非地级市还是地级市，工业用地成交价格都显著与GDP增长率正相关，并且相关性与表2中的基准回归相比相差不大，非地级市的工业用地成交价格估计系数仅仅在10%水平下显著，可能是因为样本量较小。表5的第(3)和(4)列汇报了非地级市和地级市的财政收入增长率与工业用地成交价格之间的关系，同样可以看到两组城市的工业用地成交价格都显著正向影响财政收入增长率，估计系数分别在10%、5%水平下显著。表5的最后两列给出了非地级市和地级市的房价增长率与工业用地成交价格之间的关系，依旧可以看到工业用地的价格与房价的增长率之间呈现显著的正相关关系。表5的结果说明，我们的结论不是由不同类型的地市引起的。

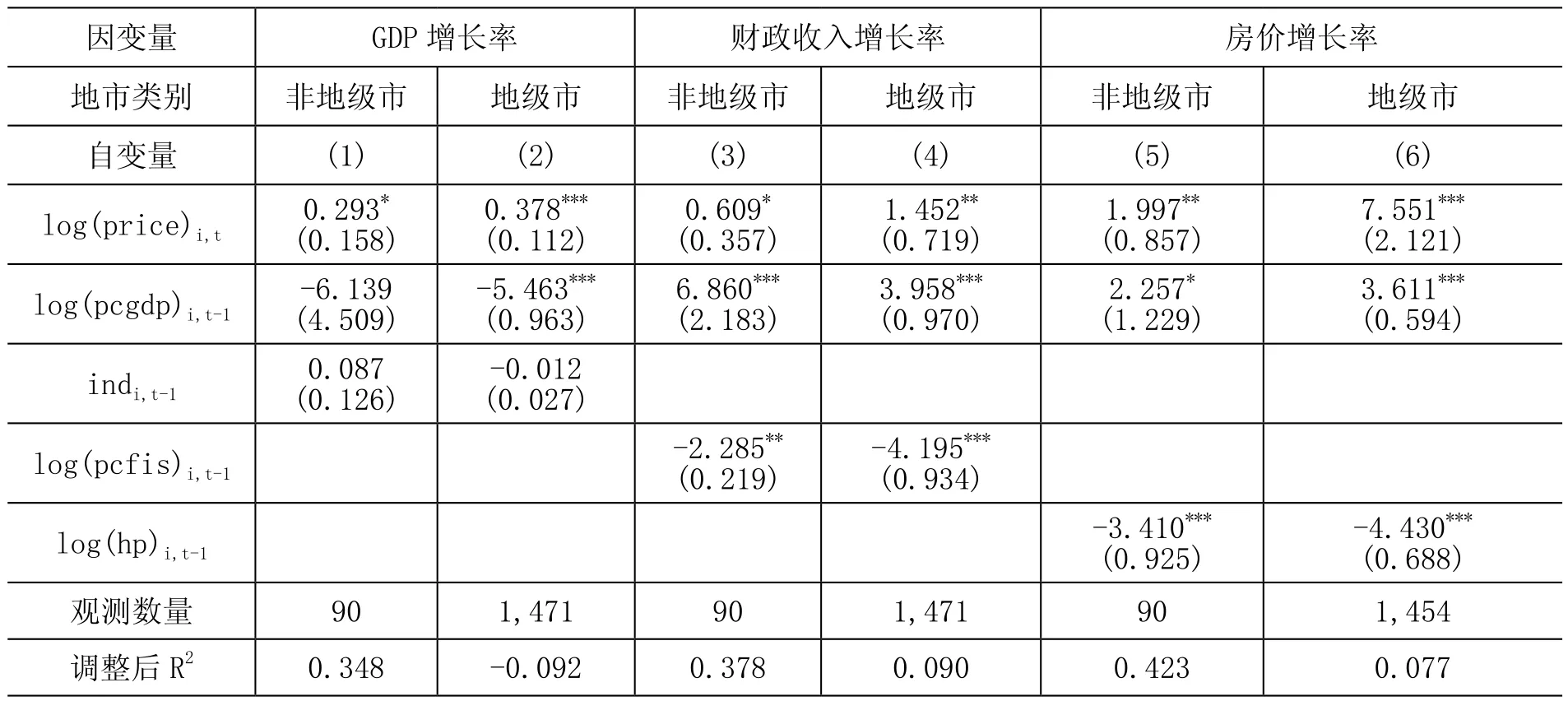
表5 子样本检验：按照城市类别划分

(2)分区域的结果

表6给出了按照朱国忠等（2014）划分的东、中、西部省份进行的分区域回归的结果。其中，东部省份包括河北、广东、山东、福建、浙江、江苏、辽宁和广西，中部省份包括山西、内蒙古、吉林、黑龙江、安徽、江西、河南、湖北和湖南，而西部省份包括四川、贵州、云南、西藏、陕西、甘肃、青海、宁夏和新疆。①由于我们考察的是地市层面的数据，直辖市没有其管辖的地市，因此四个直辖市不在考察范围内。可以看到，东、中和西部地区的地市，其经济增长率、财政收入增长率以及房价增长率都与工业用地成交价格正相关，并且估计系数与表2、表3、表4中的基准回归相差不大。这说明，我们得到的结论不是由于某一个或者几个地区的地市驱动的，结论对我国不同地区具有普适性。

表6 子样本检验：按照区域划分

2.工业用地价格的滞后效应

表7 工业用地成交价格的滞后效应

我们同时考察了工业用地成交价格的滞后效应，结果汇报于表7。可以看到工业用地成交价格的滞后项同样与GDP增长率、财政收入增长率以及房价增长率显著正相关，但是统计显著性和数值大小都弱于工业用地成交价格的当期项，这反映了工业用地成交价格的及时性会迅速影响经济社会，并且效果随着时间的推移而逐渐减弱。

表7的结果表明，我们得到的结论是可靠的，工业用地的滞后效应随着时间的推移而不断减弱，说明当期的工业用地成交价格会对经济社会带来一定的影响。

3.工业用地交易价格的内生性

表8 工业用地成交价格的内生性

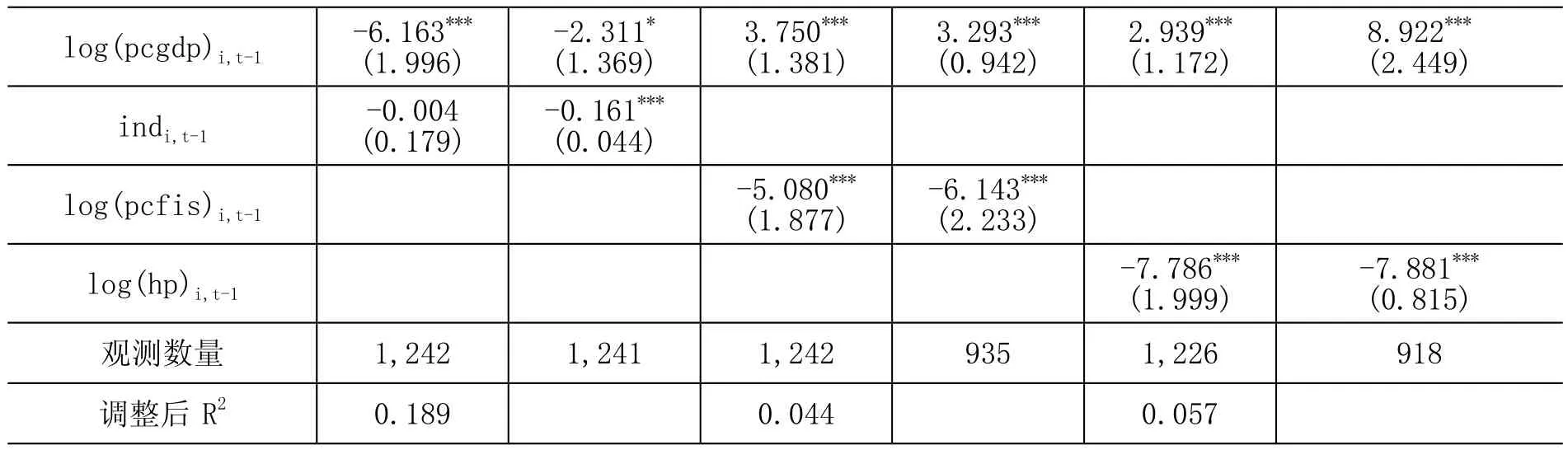
工业用地成交价格会影响经济增长、财政收入和房价的同时，这三者也同样会影响工业用地成交价格（王岳龙和张瑜，2010；黄静和王洪卫，2012），带来内生性问题，威胁到我们得到的结论，使得我们得到的估计有偏、不一致并且不准确。我们使用工具变量法和广义矩估计来克服内生性问题。

一个可信的工具变量必须与内生变量密切相关、外生（不受其他因素影响）并且不能直接影响因变量。我们发现，工业企业的数量是一个良好的工具变量。首先，工业企业的多少与工业用地成交价格相关，可以预计工业用地成交价格会因为工业企业数量的增加而提高，更多的企业竞价会推高价格。其次，由于工业企业的审批机制和准入门槛的限制，工业企业的数量会在一段时间之前确定，之后投入运营，因为这一变量是前定的（Predetermined），在面板数据中一般而言是外生的（乔坤元，2013）。最后，工业企业的数量并不会直接对经济增长率、财政收入增长率和房价增长率产生影响，企业数量本身并不重要，其经营状况才会真正对经济社会产生直接的影响。

表8子表A的第(1)、(3)、(5)列给出了第一阶段估计的结果，其他控制变量没有汇报，可以看到工业企业的数量会显著正向影响工业用地成交价格，并且估计系数在1%水平下显著。从F值来看，工具变量与内生变量的相关性较大，第一阶段的F值大于工具变量10%偏差的F值（Stock和Yogo，2002），说明本文使用的工具变量不是弱（劣）工具变量（Weak Instruments）。表8子表B的第(1)、(3)、(5)列给出了工具变量的估计结果，我们发现，在考虑到内生性问题之后，工业用地成交价格依旧正向显著影响经济增长率、财政收入增长率和房价增长率，估计系数在5%水平下显著，估计系数与基准回归得到的估计值相差不大，也说明我们的估计结果是可靠的。

然而，工具变量的有效应依旧可能受到人们的质疑，因此我们使用GMM法对方程进行估计，该方法的原理是使用因变量的高阶滞后项做工具变量进行考察（乔坤元，2013），这一组自变量避免了工具变量的问题，使得结果更加可信。我们同时使用差分GMM、水平GMM以及系统GMM法进行估计，得到了类似的结论，在这里我们仅汇报差分GMM的结果，详见表8子表B的(2)、(4)和(6)列。可以看到，虽然估计系数与基准回归以及工具变量的结果有一定的差异，但差距较小，估计系数在1%水平下显著为正，说明我们得到的结论是可靠的，在使用GMM估计方法克服内生性之后依旧成立。

表8的结果说明，即使工业用地成交价格存在内生性问题，我们的结论也是成立的，工业用地与经济增长率、财政收入增长率以及房价增长率密切正相关。

四、结论与政策建议

本文研究了我国工业用地招拍挂的竞价机制问题，说明这一机制形成的工业用地成交价格在经济社会中扮演的重要角色。我们使用拍卖模型对工业用地招拍挂的竞价机制进行建模，说明现行的一级密封价格拍卖可能会由于竞拍者故意低报自己的保留价格而造成成交价格过低的问题，继而提出使用二级密封价格拍卖机制使得竞拍者如实汇报自己的保留价格，从而提高工业用地成交价格。另外，我们讨论了两种拍卖机制的缺陷，说明避免两种拍卖制度的劣势并且引入动态拍卖程序会获得更高的拍卖价格。接着，我们使用全国所有333个地市的数据分析了现行的拍卖机制形成的工业用地成交价格对经济增长、财政收入和房价的影响，发现工业用地成交价格与三者密切正相关，这一相关性在考虑了地市差异、区域问题、价格的滞后效应以及价格的内生性问题之后依旧稳健，说明了工业用地成交价格在经济社会的重要地位。

基于本文的研究结论，我们认为政府应该考虑重新设计土地招拍挂的竞价机制，可以使用二级密封价格拍卖或者结合现行的一级和二级密封价格拍卖机制并且引入动态竞价的程序，从而最大化工业用地使用权拍卖的成交价格。另外，工业用地成交价格在经济社会中扮演的重要角色需要引起相关部门的注意。土地拍卖价格牵动着经济增长，在“土地财政”中发挥着重要的作用，这在我国发展的早期成为推动经济增长的一个重要方式，但是面对新的经济形势，谋求经济全面协调可持续发展还在于提升经济的效率，提高全要素生产率和资源的配置效率，调整经济结构。另外，工业用地成交价格对于房地产市场的影响也需要特别关注，近些年来房价的迅速上涨，部分是由投机性需求驱动，但是还有相当大的成分来自于成本的提升，土地拍卖价格带来的高成本也是促使房价迅速上涨的一个重要的因素，政府在进行宏观调控时需要注意到这一点。

[1]陈 超，柳子君，肖 辉.从供给视角看我国房地产市场的“两难困境”[J].金融研究，2011,(1).

[2]黄 静,王洪卫.土地供给方式对房价的影响研究——基于面板误差修正模型的实证分析[J].上海财经大学学报，2012,(8).

[3]况伟大,李 涛.土地出让方式、地价和房价[J].金融研究，2012,(8).

[4]李世蓉,马小刚.土地出让招拍挂制度绩效及其实证分析[J].建筑经济，2009,(4).

[5]乔坤元.IPO溢价与中签率：理论与证据[J].上海金融，2012,(9).

[6]乔坤元.非等间隔动态面板数据模型：估计方法与应用实例[J].数量经济技术经济研究，2013,(10).

[7]王宏新,勇 越.中国城市土地招拍挂制度的异化与重构[J].中州学刊，2012,(2).

[8]王岳龙.房价与地价关系的再审视——基于土地招拍挂制度的一个博弈论解释[J].学习与实践，2010,(1).

[9]王岳龙,张 瑜.基于中国省级面板数据的房价与地价关系研究[J].山西财经大学学报，2010,(1).

[10]王岳龙.土地招拍挂制度在多大程度上提升了房价？——基于“8．31”大限的干预分析模型研究[J].财贸研究，2012,(3).

[11]朱国忠,乔坤元,虞吉海.中国各省经济增长是否收敛[J].经济学（季刊），2014,(3).

[12]McAfee, Dinesh S.，Dinesh McMillan.Auctions and Bidding[J]. Journal of Economic Literature,1987, 25(2).

[13]Stock, James H.，Motohiro Yogo. Testing for Weak Instruments in Linear IV Regression[R]. NBER Working Paper No.284,2002.

（责任编辑：盛桢）

F423.2

A

2095-1280(2014)06-0085-11

刘 洋，女，北京大学光华管理学院学生。