基于HY-2高度计波形数据的高分辨率有效波高反演算法研究

王桂忠，张 杰，苗洪利，李国强，王 鑫

（1.中国海洋大学信息科学与工程学院，山东 青岛 266100；2.国家海洋局第一海洋研究所，山东 青岛 266061）

基于HY-2高度计波形数据的高分辨率有效波高反演算法研究

王桂忠1，张 杰2，苗洪利1，李国强1，王 鑫1

（1.中国海洋大学信息科学与工程学院，山东 青岛 266100；2.国家海洋局第一海洋研究所，山东 青岛 266061）

有效波高是描述海况的重要参量之一，利用高度计遥感获取有效波高已在海洋研究中获得广泛应用。本文基于海洋二号（HY-2）卫星高度计波形数据，发展了一种高分辨率有效波高反演算法，采用中误差对反演得到的20 Hz有效波高进行筛选，有效提高了测量精度。通过该方法对1个轨的波形数据进行有效波高反演，统计结果表明：与针对1 s回波反演的有效波高比较，利用该方法可将有效波高观测分辨率提高约15倍，精度约为0.44 m；利用HY-2高度计20 Hz波形数据反演的有效波高精度可靠，可用其进行高分辨率的相关海洋研究。

HY-2；有效波高；反演算法；高分辨率

1 前言

海洋二号（HY-2）卫星高度计是我国第一个专用于海洋科学研究的星载雷达高度计。自2011年发射以来，HY-2高度计提供了大量的海面观测数据，包括海表面高度、风速和有效波高等[1]。其中有效波高是描述海况的重要参量之一。

卫星雷达高度计向星下点海面发射雷达脉冲，经海表面后向散射后，根据不同时刻接收到的回波功率得到回波波形。有效波高可通过回波波形前沿斜率获取，前沿斜率越大，相应的海面波高值就越小；反之，相应的海面波高值就越大[2]。

张有广等[3]在Barrick[4]海面回波散射模型的基础上，利用机载高度计数据进行了有效波高快速反演算法的研究。纪永刚等[5]利用神舟四号的高度计数据，通过波形拟合的方法进行了有效波高的反演研究。李秀仲等[6]基于HY-2机载校飞数据，采用最小二乘拟合的方法提取了有效波高信息。以上研究均是针对1 s的平均波形反演的平均有效波高。而高度计回传的是20 Hz信号，即每0.05 s回传1个波形数据。针对20 Hz波形数据进行高分辨率有效波高反演的研究至今未见报道。本文通过高度计20 Hz（0.05 s）波形数据，采用新的反演算法对其有效波高进行反演，获取高时空分辨率的有效波高。

2 数据采集

本文采用的波形数据为HY-2高度计1B数据产品，该数据产品可提供20 Hz波形数据，即1 s可提供20个回波波形，每个回波时间间隔为0.05 s，下文统称为20 Hz波形数据。但该数据产品中并无每个回波的精确经纬度信息，因此无法获得20 Hz数据的空间分辨率。Jason-2的传感器地球物理数据集（SGDR）数据产品提供了每个回波的经纬度信息，其时间间隔为0.05 s，空间距离约为580 m，这使得利用波形数据进行高分辨率海洋研究成为可能。

3 有效波高反演算法

3.1 有效波高反演流程

本文将20 Hz实测回波波形与模型计算得到的波形进行拟合，反演有效波高，并对反演得到的有效波高添加中误差筛选条件来提高精度，具体流程如图1所示。输入数据为HY-2高度计波形数据，该流程图中天线指向角的计算方法参考徐曦煜等[7]采用的方法，下面分别介绍本方法的其他相关技术。

图1 有效波高反演流程图Fig.1 The significant wave height inversion flowchart

3.2 波形归一化

利用高度计回波波形的前沿斜率反演有效波高需将有效波高进行归一化处理，将单个波形每个采样门值除以该波形中采样门最大值，完成波形归一化，具体如式（1）

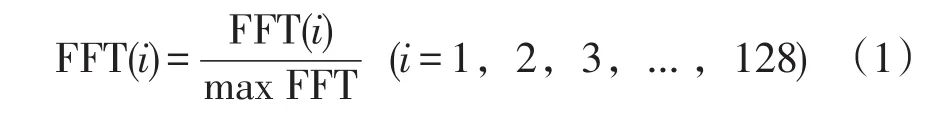
式（1）中，FFT(i)为采样门值，max FFT为所有采样门中的最大值。

3.3 波形筛选

波形筛选是为了剔除异常回波，如受陆地、海冰等污染的回波信号。本文采用下面3个条件来筛选波形。

1）计算每一个20 Hz波形的上升沿起始点与最大值点的位置，根据这两点求波形的半功率点位置。正常的海洋回波波形半功率点在32.5左右，设定阈值为3，如果20 Hz波形的半功率点与32.5的差值超过阈值，则将波形剔除。

2）考虑到回波波形在上升沿存在振荡，使得反演的有效波高与实际相差很大，因此取上升沿以后连续7个点，判断其波形值是否是连续增加的，如果不满足，则将其剔除。

3）最后一个采样门对应的波形值如果大于波形前沿最大值，则视为异常波形。

3.4 热噪声去除

去除热噪声首先要确定波形上升沿起始位置，比较4个连续的采样门值，如果4个采样门值是递增的，即从第2个采样门开始每个采样门值都比前一个值大，则取第1个采样门的位置为上升沿的起始点。求出波形上升沿以前连续且稳定的5个采样门值的平均估计热噪声分量，每个采样门值减掉该分量，从而去除热噪声。

3.5 波形拟合

波形拟合是将实测回波波形与模型计算波形进行拟合，通过使拟合差值最小来计算得到有效波高。本文基于Hayne模型[8]得到计算波形并与实测波形拟合。雷达高度计的回波波形理论模型表示为

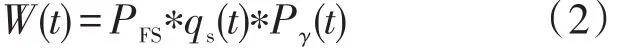
式（2）中，W(t)为接受回波的平均功率；PFS(t)为平坦海平面平均雷达脉冲响应函数；qs(t)为海面镜像点概率密度函数；Pγ(t)为雷达系统点目标响应函数。

Hayne给出了该卷积模型中各项的解析表达式[8]。其中，平坦海平面平均雷达脉冲响应函数PFS(t)的解析式如式（3）

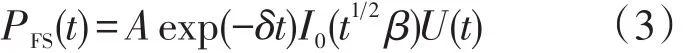
其中

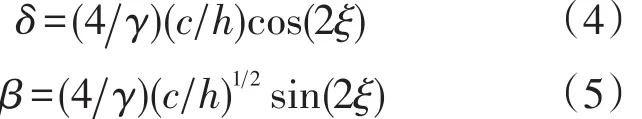
海面镜像点概率密度函数qs(t)的解析式如式（6）

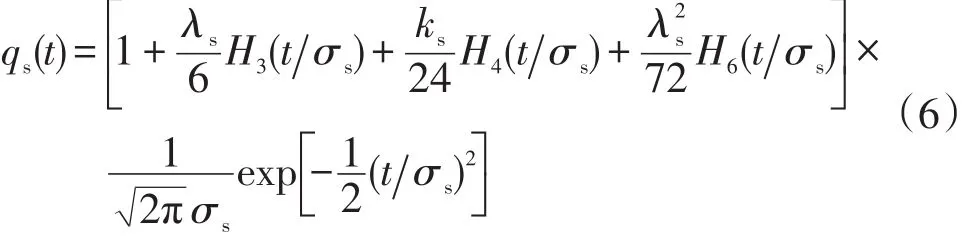
式（6）中，σs为表面波高均方根值；λs为偏斜量；ks为峰度；Hi（i=3，4，6）为Hermite多项式。

雷达系统点目标响应函数Pγ(t)的解析式如式（7）

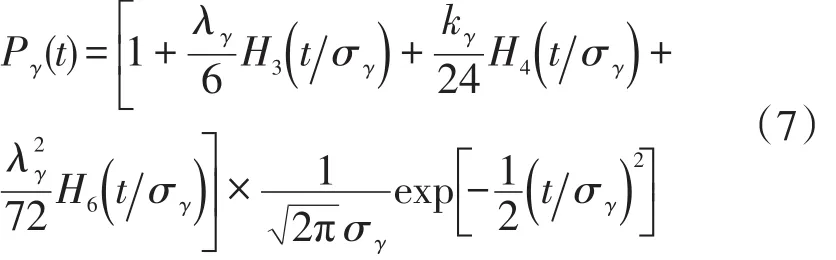
式（7）中，σγ、λγ和 kγ分别是上升时间、偏斜量和峰度。

由式（2）、式（3）、式（6）和式（7）可得回波模型的解析表达式为

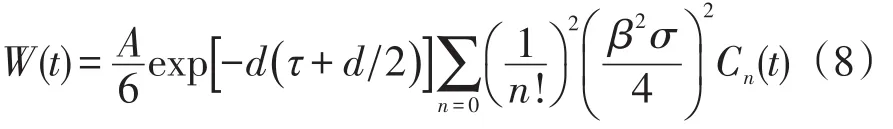
式（8）中各参量展开如下

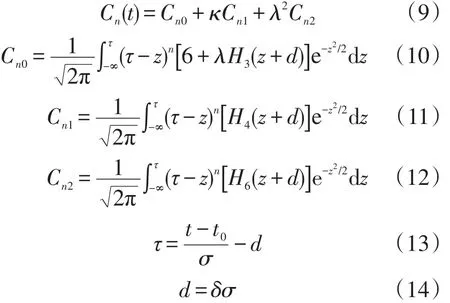
把高度计的实测波形与Hayne回波模型进行带权的最小二乘拟合，使得拟合差值最小，即得到时间参数，从而计算得到有效波高。

3.6 中误差筛选条件

为了保证20 Hz有效波高的精度，对利用上述方法得到的20 Hz有效波高再添加中误差筛选条件。将高度计1 s有效波高作为参考值，根据与之对应的20 Hz有效波高与其残差的范围进行筛选。本文选取1倍和2倍中误差作为筛选条件，中误差计算公式如式（15）

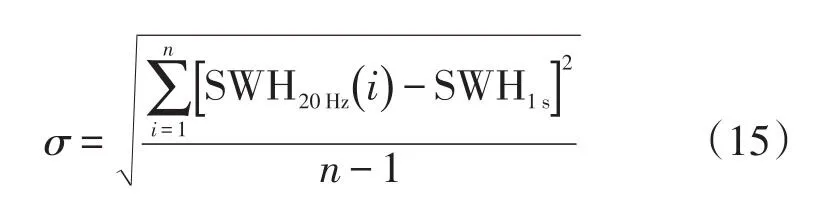
式（15）中，n为1 s内有效波高的个数，SWH1s为1 s有效波高值。

4 结果分析

利用上述方法对HY-2高度计第21重复周期的第3轨波形数据反演有效波高并进行统计分析，该轨共有2677个测量数据。根据数据手册编辑标准，满足下面两个条件的数据列入统计范围：a.有效波高值在0～11 m之间；b.满足条件a的有效波高在1 s内不小于5个。满足上述条件的数据共有2009个。

HY-2高度计的1 s有效波高的测量值精度较高，因此，通过绘制不同条件下20 Hz有效波高与对应的1 s有效波高的散点图来分析其相关性，结果如图2所示。其中，图2a为未添加筛选条件的情况，其1 s有效波高与20 Hz有效波高相关系数（R）为0.8925；图2b为添加2倍中误差筛选条件（即剔除20 Hz有效波高与1 s有效波高差值大于2倍中误差的数据）后的情况，两者相关系数提高至0.9322。这说明添加中误差筛选条件可以明显提高20 Hz有效波高与1 s有效波高的相关性。

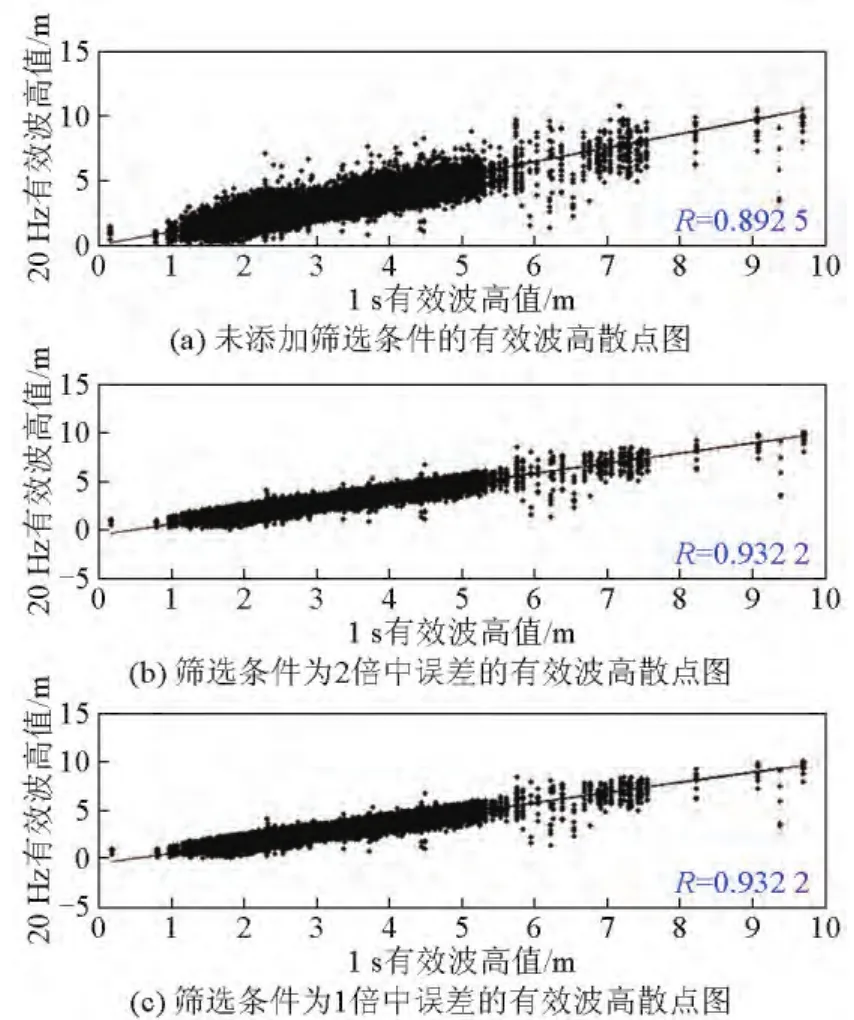
图2 不同条件下有效波高散点图Fig.2 The significant wave height scatter plot under different conditions

图2c为添加1倍中误差（即剔除20 Hz有效波高与1 s有效波高差值大于1倍中误差的数据）筛选条件后的情况，相关性无改善，与添加2倍中误差筛选条件的情况相同。这说明该轨所有20 Hz有效波高与对应的1 s有效波高的差值均在1倍中误差之内，反映了HY-2高度计20 Hz波形数据的精度较高，这在下面的分析中也进一步得到证明。

分别针对上述3种情况，统计1 s数据个数、20 Hz波形平均数及标准偏差，结果如表1所示。

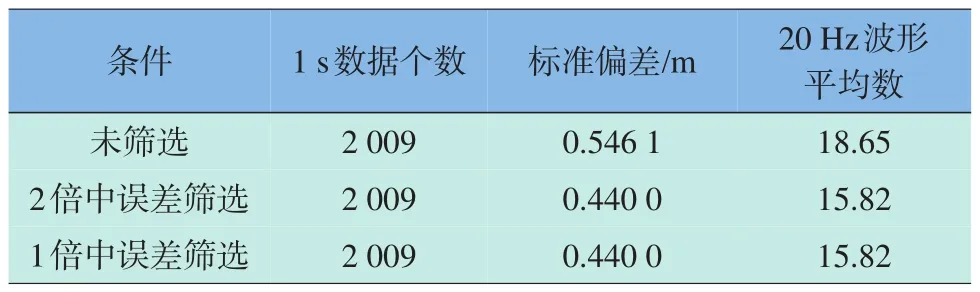
表1 不同条件下的数据统计情况Table 1 Statistics under different conditions

从表1可以看出，添加筛选条件对1 s有效波高数据个数没有影响，这也说明HY-2高度计20 Hz波形数据精度较高，即1 s内至少有5个波形数据可通过其反演得到在0～11 m之间的有效波高；添加2倍中误差筛选条件后的标准偏差由0.5461 m降为0.4400 m，说明2倍中误差筛选条件有效提高了20 Hz有效波高的精度；1倍中误差筛选条件和2倍中误差筛选条件两种情况下的标准偏差相同，再次说明HY-2高度计波形数据精度较高；虽然1 s内20 Hz波形平均数由18.65降为15.82，但相对于1 s有效波高，其分辨率的提高依然是巨大的。

5 结语

1）本文基于HY-2波形数据发展了一种高分辨率有效波高反演算法，利用该算法反演的有效波高时空分辨率较1 s有效波高可提高约15倍，精度约为0.44 m。

2）分别对该算法反演得到的有效波高添加1倍中误差和2倍中误差筛选条件并统计标准偏差，发现两者标准偏差相同，这表明利用该算法反演得到的有效波高精度较高。

3）利用本算法反演得到的有效波高可进行高分辨率相关海洋研究。

致谢

感谢国家卫星海洋应用中心提供数据。

[1]蒋兴伟，林明森，宋清涛.海洋二号卫星主被动微波遥感探测技术研究[J].中国工程科学，2013，15(7)：4-11.

[2]Fu Lee-Lueng，Cazenave Anny.Satellite Altimetry and Earth Sciences：A Handbook of Techniques and Applications[M].Massachusetts：Academic Press，2001.

[3]张有广，张 杰，纪永刚.机载高度计获取有效波高快速反演算法研究[J].海洋科学进展，2002，20(4)：5-10.

[4]Barrick D.Remote sensing of sea state by radar[C]//Ocean 72-IEEE International Conference on Engineering in the Ocean Environment.New York：The Institute of Electrical and Electronic Engineering，1972：186-192.

[5]纪永刚，张 杰，张有广.神舟四号高度计有效波高反演[C]//第十四届全国遥感技术学术交流会论文摘要集.青岛，2003：79-80.

[6]李秀仲，张有广，孟俊敏.基于HY-2卫星高度计机载校飞数据的有效波高信息提取及初步分析[J].海洋科学进展，2012，30(2)：212-218.

[7]徐曦煜，刘和光.高度计姿态角估计算法误差分析[J].中国科学院研究生院学报，2008，25(1)：54-60.

[8]Hayne G S.Radar altimeter mean return waveforms from nearnormal-incidence ocean surface scattering[J].Antennas and Propagation，IEEE Transactions on，1980，28(5)：687-692.

Research on inversion algorithm of significant wave height with high resolution based on waveform data from HY-2 altimeter

Wang Guizhong1，Zhang Jie2，Miao Hongli1，Li Guoqiang1，Wang Xin1

(1.College of Information Science and Engineering，Ocean University of China，Qingdao，Shandong 266100，China；2.First Institute of Oceanography，SOA，Qingdao，Shandong 266061，China)

Significant wave height(SWH)is one of the important parameters which describe the sea state.The SWH derived from altimeter has been widely applied in marine research.Based on waveform data from HY-2 altimeter，we developed an inversion algorithm of SWH with high resolution.The root mean square error(RMSE)condition was used to improve the accuracy of 20 Hz SWH.By applying this method in the waveform data of one pass，the result showed that the inversion algorithm is effective.Compared with the SWH derived from 1 s waveform，the spatial and temporal resolution of the SWH derived by this method could be increased by about 15 times and the accuracy is about 0.44 m.The SWH derived from HY-2 altimeter 20 Hz waveform is reliable and could be applied for high resolution marine research.

HY-2；significant wave height；inversion algorithm；high resolution

P731.22；P228.3

A

1009-1742(2014)06-0060-05

2014-04-10

国家自然科学基金项目（41176157）

苗洪利，1964年出生，男，山东青岛市人，教授，主要研究方向为海洋遥感；E-mail：oumhl@ouc.edu.cn