一种新型基于格基约减的MIMO 检测算法

刘晓光，鲍亚川，苏 斌，张 帆，段世刚

(1.甘肃省电力公司 信息通信公司，甘肃 兰州 730050;2.西安电子科技大学 通信工程学院，陕西 西安 710071)

新兴的通信业务对数据速率、频谱效率的要求越来越高，下一代宽带无线接入系统不仅采用了多输入多输出(Multiple Input Multiple Output，MIMO)技术。MIMO 技术在LTE－A 系统中已得到了广泛应用，该技术可显著提高数据传输的速率。随着MIMO 技术的发展，对检测技术也提出了更高的要求。近年来对MIMO 检测算法的研究也在不断发展。

现有的MIMO 检测算法主要分为两类:非线性检测算法和线性检测算法。非线性检测算法主要有最大似然检测(Maximum Likelihood，ML)、球域检测(Spheroid Detection，SD)［1－2］、树搜索［3］和最大似然搜索［4］等;线性检测算法主要是ZF/MMSE［5］。相对线性检测方法，非线性检测具有优良的性能，但计算复杂度较高，在实际的多用户通信环境中难以应用。将格基约减理论应用到MIMO 检测中可获得良好的效果，文献［6 ～13］提出了各种基于格基约减的检测算法。目前较为典型的基于格基约减算法主要有LLL 算法和Seysen 算法。MIMO 检测算法的性能和复杂度之间具有一定的关系，但当对待检测的信号进行一定的预处理后，在一定的计算复杂度下可取得更好的效果。本文在传统检测和基于格基约减检测的基础上，将OSIC(Ordered Successive Interference Cancellation)与格基约减算法相结合，并引入K－best 算法的思想，提出了一种新型的格基约减算法(KLR_OSIC)。与原有基于格基约减的检测算法相比，其改进算法在有效降低算法复杂度的同时，也显著提高了MIMO 检测性能。

1 系统描述

在一个MIMO 系统中，发射天线数为Nt，接收天线数为Nr，其系统模型可用式(1)表示

其中，x∈ΩNt是发送信号向量;y∈CNr是接收信号向量;H=［h1，h2，…，hNt］代表平坦衰落信道的信道矩阵，向量hi(i=1，2，…，Nt)服从均值为0、方差为1 的复高斯分布;n∈CNr是方差为的高斯白噪声;集合Ω是经过M－QAM 调制后的星座点集合，集合C 代表复数域。整个系统框图如图1 所示。

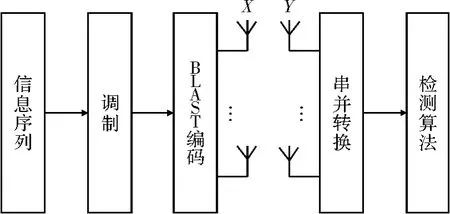
图1 系统框图

2 格基理论和基本算法

2.1 格基理论

格基约减(Lattice Reduction)是格理论中解决近似最短向量问题的一种方法。格基约减就是对格生成矩阵B 的各列进行一系列迭代的模值比较和约减处理，然后得到一组基，而这组基中会包含近似的最短向量。格基的另一个性质是:若一组基向量长度较短，则这组基向量之间将接近正交。因此格基约减在缩小格基模值的同时，也提高了基向量之间的正交性。

将格以及格基约减理论应用于MIMO 检测问题，信道矩阵H 可理解为格的生成矩阵B，发送信号x 可理解为生成格的系数矢量，接收端收到的信号y 便可理解为Hx 由生成的格点加噪后的结果，则检测问题就变为由格点y 和格生成矩阵H 推算系数x 的过程。如图2 显示了两个不同格基产生的格点分布。变换后的格点分布更均匀，这意味着可准确判决的区域更大，因此将格基约减应用到MIMO 信号的检测中，能显著提升检测的性能［14－15］。

图2 格点分布对比

2.2 基本算法

迫零算法(ZF)和线性最小均方误差(MMSE)算法是两种基本的算法，二者均是在检测对检测量乘以一个滤波矩阵，最终检测出所需信号。

串行干扰消除(SIC)的主要思想是:先检测出某一天线的信号，然后将该信号造成的干扰从待检测信号中消除，并逐次迭代。

球形译码算法的原理和最大似然检测算法相同，其改进之处在于通过条件限制压缩搜索区域。

基于格基约减的算法中，常用的有LLL 算法和Seysen 算法。

3 KLR_OSIC 算法的原理及步骤

在MIMO 检测中，对检测结果误码率影响最大的是信噪比最差的信号，因此若能够尽可能地保证信噪比最差信号的检测准确度，最终的检测输出将会更加准确。每层信号的信噪比与信道矩阵H 进行QR 分解后的上三角矩阵R 中对角元素的绝对值成正比，所以在考虑排序的串行干扰消除算法中，要在QR分解过程中同时完成对R 的排序，则在SIC 检测过程中就会先对信噪比较高的信号进行检测。

KLR_OSIC 算法中也引入了SIC 来提高性能。但不同之处在于KLR_OSIC 引入了K－best 的思想，则以优先确保信噪比最差的信号检测准确度为出发点，在QR 分解的过程中，对R 中元素的排列顺序与传统OSIC 相反，即将R 的对角元素Rk，k从1 ～Nt逐渐变小，然后对低信噪比信号先进行大概估计，并以此为依据对其取候选集，根据候选集对高信噪比信号进行检测，最后在所有的候选检测结果中选出最终结果。这样做本质上仍是先对高信噪比信号进行检测，且在这一过程中去除部分低信噪比信号的干扰，提高了对高信噪比信号的检测准确度，同时由于候选集的引入，低信噪比信号检测的准确度得到明显提高，最终大幅提高了整个算法的检测性能。因为这种改进型的格基约减算法综合了格基约减、K－best 和OSIC 的思想，所以称之为KLR－OSIC 算法。这里以发射天线和接收天线数均为4 的MIMO 系统为例来进行介绍。调制方式为M－QAM，接收信号模型为式(1)。

整个步骤可分为3 部分:第一部分为分层，步骤1为这一部分的操作;第二部分为格基检测，步骤2、3 为这一部分的操作;第三部分为K－best 检测，步骤4、5为这一部分的操作。

步骤1 对H 进行QR 分解，记为H=QR，则式(1)可化为

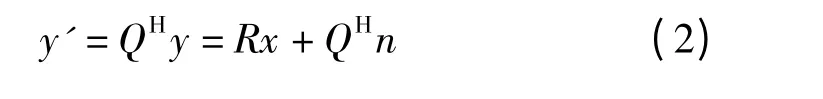
然后对系统进行分层处理，将其分为两层，如式(3)所示

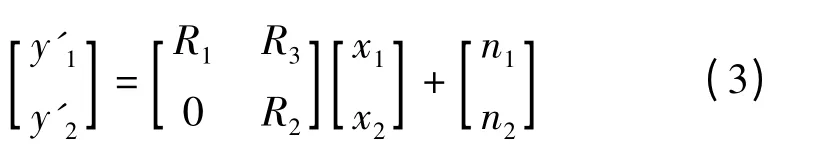
其中y'1，y'2，x1，x2为2×1 的列向量;R1，R2，R3为2×2 的矩阵。则式(3)可写为两层:第一层

第二层

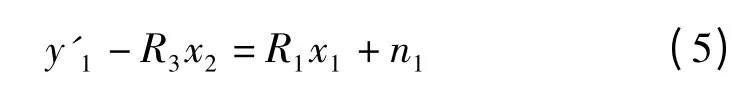
步骤2 是对第一层进行基于格基约减的检测计算，可采用ZF_LR 算法或MMSE_LR 算法，获得在约减域中的估计结果

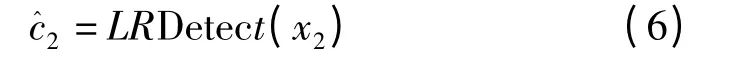
步骤4 根据候选集中的每个候选向量，对第二层进行基于格基约减的检测则

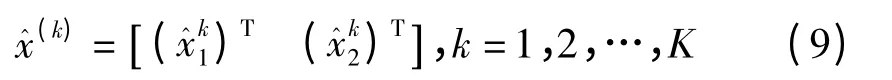
步骤5 根据式(12)从K 个候选结果中选出最终的检测输出结果为

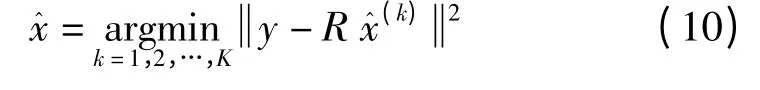
4 系统仿真

对MIMO 检测算法的性能进行仿真研究。仿真中采用4×4 的MIMO 系统，调制方式为16 QAM，信噪比范围为0 ～20 dB，仿真间隔2 dB，每次5 000 帧，每帧中包含4 个符号。图3 为对系统采用ZF、ZF－LLL、ZF－Seysen、MMSE、MMSE－LLL、MMSE－Seysen 及ML 算法的仿真结果。图4 为对系统采用KLR_OSIC算法、MMSE、MMSE－LLL 及ML 算法进行检测的仿真结果，其中K 值分别取为4、8 和12。

如图3 所示，ML 是最优的检测算法，MMSE 居中，ZF 最差。引入格基约减的ZF－LLL、ZF－Seysen、MMSE－LLL、MMSE－Seysen 算法比ZF 和MMSE 的性能要好，且4 种算法均优于MMSE 算法。因此Seysen的算法相比采用LLL 的算法效果更佳。

图3 16 QAM 调制下基于格约减检测算法性能

如图4 所示，KLR_OSIC 算法在K 值取4 时，其性能弱于MMSE_LLL 算法，但当K=8 时则超过了MMSE_LLL 检测性能，K=12 时与ML 算法性能接近。可看出不同的K 值其算法性能也不同。分析可知，K值越大，计算复杂度越高。

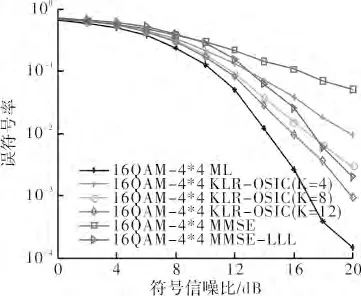
图4 16 QAM 调制下KLR_OSIC 算法性能曲线

5 结束语

本文所提的KLR_OSIC 与传统的基于格基约减的算法，在高维度的MIMO 检测系统中具有较大优势。其首先解决了高维矩阵应用格基约减的运算复杂度高的问题，其次通过对H 进行灵活的分层，以及灵活分配每一层的候选集个数，从而在算法的复杂度和检测性能之间获得最佳的折衷。

［1］ HASSIBIAND B，VIKALO H.On the sphere－decoding algorithm I.Expected complexity［J］.IEEE Transactions on Signal Processing，2005，53(8):2806－2818.

［2］ VIKALO H，HASSIBI B.On the sphere－decoding algorithm II.Generalizations，second－order statistics，and applications to communications［J］.IEEE Transactions on Signal Processing，2005，53(8):2819－2834.

［3］ DE JONG Y L C，WILLINK T J.Iterative tree search detection for MIMO wireless systems［J］.IEEE Transactions on Communications，2005，53(6):930－935.

［4］ VISHNU VARDHAN K，SAIF K MOHAMMED，CHOCKALINGAM A，et al.A low－complexity detector for large MIMO Systems and multicarrier CDMA Systems［J］.IEEE Journal on Selected Areas in Communications，2008，26(3):473－485.

［5］ WOLNIANSKY P W，FOSCHINI G J，GOLDEN G D，et al.V－BLAST:An architecture for realizing very high data rates over the rich－scattering wireless channel［C］.In Proceeding IEEE ISSSE，1998:295－300.

［6］ MA X，ZHANG W.Performance analysis for MIMO systems with lattice reduction aided linear equalization［J］.IEEE Transactions on Communication Technology，2008，56(2):309－318.

［7］ NGUYEN P Q，VALLÉE B.The LLL algorithm:survey and applications berlin［M］.Germany:Springer－Verlag，2010.

［8］ WÜBBEN D，BÖHNKE R，KÜHN V，et al.MMSE－based lattice reduction for near－ML detection of MIMO systems［C］.Proceeding ITG Workshop Smart Antennas(WSA)，2004.

［9］ WÜBBEN D，SEETHALER D，JALDEN J，et al.Lattice reduction:a survey with applications in wireless communications［J］.IEEE Signal Processing Magazine，2011，28(3):70－91.

［10］孙艳华，王浩，张延华.复数域格缩减的MIMO 检测算法研究［J］.电子科技大学学报，2010，39(5):670－675.

［11］NIU T.A comparison of two lattice－reduction－based receivers for MIMO systems［C］.Sarnoff Symposium，2008:1－6.

［12］AUBERT S，NASSER Y，NOUVEL F，et al.Lattice reduction aided minimum mean squareerror k－best detection for MIMO Systems［C］.ICCNC.Wireless Communications Symposium，2012:1066－1070.

［13］WUBBEN D，BOHNKE R，RINAS J，et al.MMSE extension of V－BLAST based on sorted QR decomposition［C］.Florida，USA:IEEE VTC2003－Fall，2003.

［14］钱荣荣，漆渊，彭涛，等.MIMO 系统中低功耗性能最优的球译码［J］.北京邮电大学学报，2011，34(1):90－93，115.

［15］LUIS G B，RATNARAJAH T，COLIN C.A comparison of complex lattice reduction algorithms for MIMO detection［C］.IEEE ICASSP，2008:2705－2708.