三轴稳定卫星姿态可视化绘制与建模
淡 鹏,张定波,王 丹,李万山
(1.宇航动力学国家重点实验室 软件室,陕西 西安 710043;2.西安卫星测控中心,陕西 西安 710043)
航天测控视景可视化技术为航天器在轨运行状况提供了直观的表达方式,在航天飞行任务中得到了越来越多的应用。而在众多航天器中,三轴稳定卫星是数量较多的一类,因而此类航天器运行场景的可视化绘制就显得尤为重要。而对其进行的可视化绘制中最基本的就是位置与姿态信息的呈现。而姿态数据相对位置信息而言,其形式众多,变化多样,实现较为复杂。文献[1 ~6]对姿态数据绘制方法有一定涉及,但均较少给出了系统全面的介绍。为此,本文对三轴稳定卫星姿态信息各类常用表达方式及可视化建模技术进行了研究,并基于三维视景系统常用的OpenGL 图形库[7]对其绘制过程进行了可视化实现。
1 姿态绘制参考系与基准坐标系
在三轴稳定卫星姿态可视化绘制实现中,常用的参考系有:地心固连系、J2000 地心惯性系[8]、质心轨道系、东南地坐标系及卫星本体系等。
(1)质心轨道坐标系OXOYOZo:坐标原点位于卫星质心,ZO轴指向地心,YO轴垂直于轨道面,指向轨道角速度的负方向,XO轴由右手法则确定。
(2)东南地坐标系OXEYSZD:坐标原点位于卫星质心,ZD轴指向地心,XE轴在指向卫星当地东,YS轴指向卫星当地南。
(3)卫星本体坐标系OXBYBZB:此坐标系与卫星固连,原点为卫星质心,XB在纵对称面内指向卫星头部,ZB在纵对称面内与XB垂直且指向地,YB由右手法则确定。
为了便于对卫星运行整个场景中各类对象的绘制,在可视化实现中需要将一副场景内各个对象的模型构建和图形绘制建立在统一的基准坐标系下。为此,本文采用地心固连系及J2000 地心惯性系作为可视化绘制的基准坐标系。在三维绘制中,对这两个坐标系的变换可近似于只考虑恒星时角的区别,即相互变换时只需绕Z 轴旋转一角度(格林尼治恒星时角[8])即可。
2 姿态绘制与建模
2.1 欧拉角姿态
三轴稳定卫星姿态数据常使用卫星本体系相对姿态参考系的3 个欧拉角表示。对此类姿态数据进行可视化绘制时,需通过两次模型变换来完成,首先是可视化绘制的基准系(地固系或地心惯性系)到姿态参考系的旋转变换(设变换矩阵为MER),其次是姿态参考系到卫星本体系的旋转变换(设变换矩阵为MRB)。完整的绘制基准坐标系到本体系变换矩阵为M=MRB·MER。
设当前时刻卫星姿态3 个欧拉角为:俯仰角θ、偏航角Ψ、滚动角φ,则3-2-1 转序下姿态参考系到本体系变换方法为:(1)绕z 轴旋转Ψ。(2)绕y 轴旋转θ。(3)绕x 轴旋转φ。变换矩阵可用下式表示:MRB=RX(φ)RY(θ)RZ(Ψ)。
使用OpenGL 进行可视化绘制时,此变换用齐次坐标模型变换方法可表达为
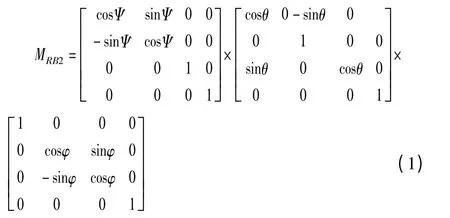
需要说明的是,矩阵MRB2为使用OpenGL 绘制时采用的模型变换矩阵,与实际轨道姿态计算中进行的坐标变换的变换顺序相反,具体可见文献[9]中关于OpenGL 的视图模型变换部分。即与变换矩阵MRB矩阵相乘顺序不同。
具体可视化实现时,也可直接通过下面的OpenGL旋转变换语句实现:

另外,需注意的是欧拉角姿态有多种转序的定义,除了3-2-1 转序外,常用的还有3-1-2 转序等,变换时需根据所用欧拉角具体的转序定义进行操作。当使用3-1-2 转序时,变换矩阵MRB可表示为MRB=RY(θ)RX(φ)RZ(Ψ)。
对绘制基准坐标系到姿态参考系的变换,根据参考系的不同而有所区别。在三轴稳定卫星姿态计算中较多使用的姿态参考系有质心轨道坐标系和东南地坐标系等。
当卫星姿态建立在质心轨道坐标系下时,姿态模型变换计算可通过下面两种方法实现:
方法1 多次旋转法。
若已知当前点的轨道根数a,e,i,Ω,ω,M(分别为半长轴、偏心率、倾角、升交点赤经、近地点幅角、偏近点角),则可由M 和e 计算出真近点角f[7],此时,地固系到姿态参考系变换方法为:(1)绕z 轴旋转Ω-s(s 为当前时刻零度经线格林尼治恒星时角);(2)绕x轴旋转i;(3)绕z 轴旋转ω+f+π/2;(4)绕x 轴旋转-π/2。变换过程可表示为
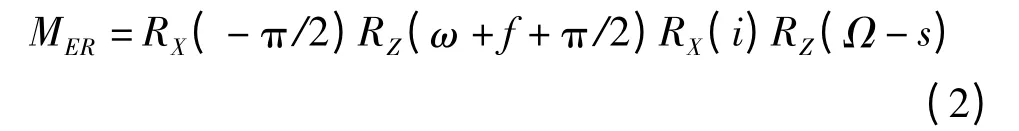
整个旋转过程可用OpenGL 语句表达为
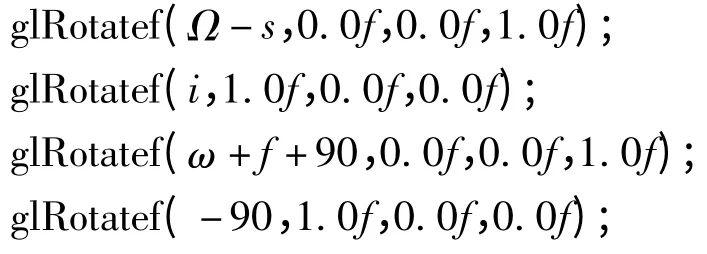
方法2 转换矩阵法。
若已知卫星当前J2000 惯性系位置rECI和速度,则根据质心轨道系的定义,可得到其三轴方向在J2000 惯性系下的方向矢量分别为
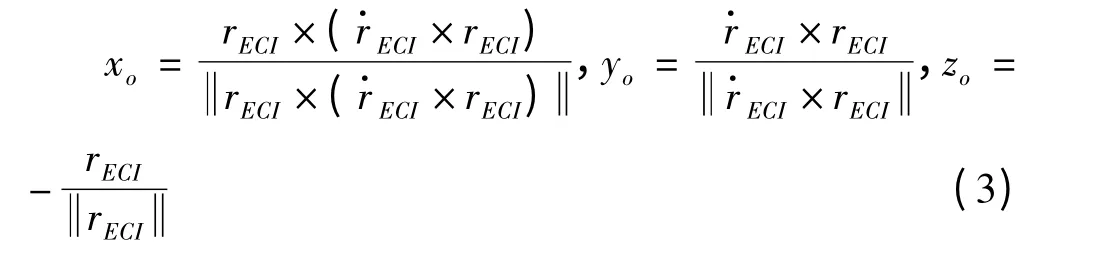
则J2000 地心惯性系到质心轨道坐标系的坐标变换矩阵为MER=[xo,yo,zo]T。此时,以地固系为基准系的姿态变换方法为:(1)绕z 轴旋转-s(s 为恒星时角)将其变换成J2000 惯性系。(2)乘以变换矩阵M(需将其扩充为4×4 的齐次旋转矩阵)。以地心惯性系为基准系时省略掉第一步变换即可。
变换过程用OpenGL 语句可表示为:
glRotatef(-s,0.0f,0.0f,1.0f);
glMultMatrixf(MER)
当卫星姿态参考系建立在东南地坐标系下时,变换方法为:
方法1 多次旋转法。根据三轴稳定卫星的位置坐标可计算出位置矢量的赤经α 和赤纬δ,则以J2000惯性系开始的姿态模型变换方法为(1)绕z 轴旋转α;(2)绕y 轴旋转-δ;(3)绕Z 轴旋转π/2;(4)绕x 轴旋转-π/2。用公式可表示为
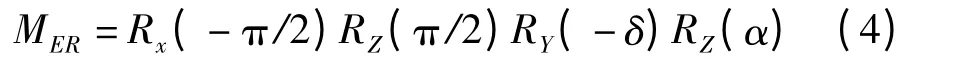
方法2 转换矩阵法。由位置矢量可得到东南地坐标系三轴在J2000 惯性系下方向矢量分别为
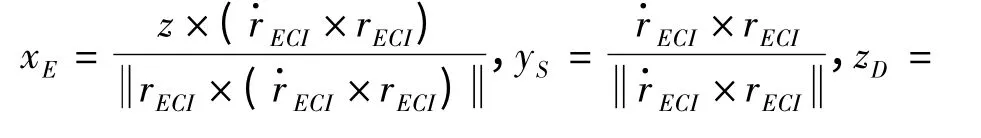

其中,z=(0 0 1)T则J2000 惯性系到东南地坐标系坐标变换矩阵为MER=[xE,yS,zD]T,此时进行绘制时,乘以变换矩阵MER即可。
2.2 四元数姿态
由Hamilton 发明的四元数[10-11](Quaternio-n)是复数在四维实数空间的一个推广,亦是卫星姿态的一类重要的表示方法。
设一单位四元数为q=q0+q1i+q2j+q3k,其中q0为四元数的标部,q1、q2、q3为其矢部,则由该单位四元数确定的姿态转换矩阵为
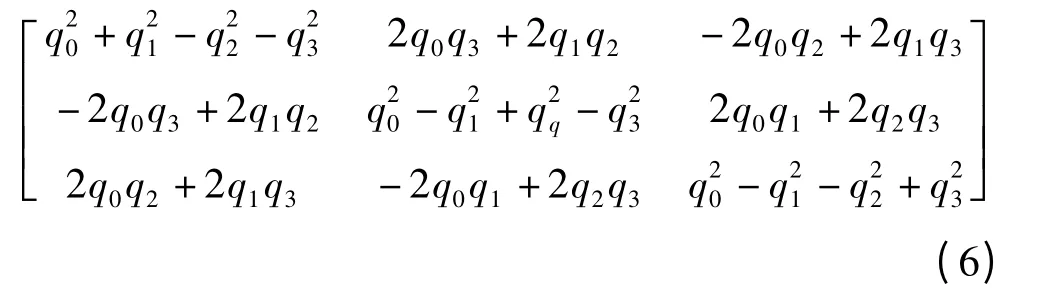
据此即可对姿态数据进行可视化绘制。
另一种方法是将四元数姿态转换成欧拉轴角形式,设欧拉轴在参考系中的矢量为E,转角为α,则四元数也可定义为
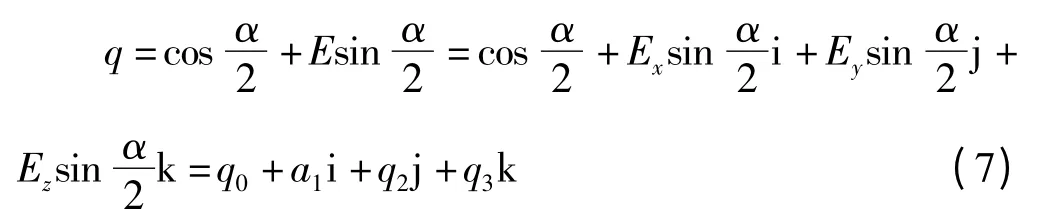
根据此定义公式,由四元数值可解算出单次旋转的欧拉轴及转角:转角为α=2cos-1(q0)。当α≠0 时,有旋转轴矢量为
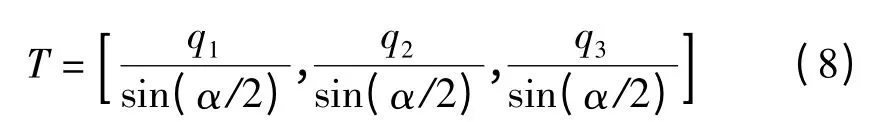
由该旋转轴及旋转角度调用OpenGL 旋转语句即可简单地对四元数姿态进行可视化绘制。
2.3 其它姿态形式
除了常用的欧拉角、四元数表示形式外,常见的姿态描述方法还有欧拉轴/角式、方向余弦式等。
对欧拉轴/角姿态描述,其直接定义了旋转轴及转角,可直接调用OpenGL 的旋转语句进行绘制。而对方向余弦表示,可给出两个坐标系间的转换矩阵[8],继而调用OpenGL 的矩阵运算语句进行绘制。
2.4 姿态球绘制
三轴稳定卫星姿态可视化绘制的一种常用表达方式就是姿态球,其在深空探测等场合中有着广泛应用。
姿态球一般定义在惯性系下,对于四元数或欧拉角姿态,可由上述多次旋转方法进行三轴指向的绘制。也可计算出惯性系到本体系的转换矩阵M,进而得到卫星三轴方向在惯性系下的方向矢量或各轴指向的赤经、赤纬,即可进行姿态球绘制。其中,x 轴矢量为X=M·[1 0 0]T;y 轴矢量为Y=M·[0 1 0]T;z 注矢量为Z=M·[0 0 1]T。
设x 轴单位矢量的3 个分量为X[0]、X[1]、X[2],则x 轴赤经为∂=tan-1(X[1]/X[0]),赤纬为δ=sin-1(X[2]),y 轴、z 轴赤经赤纬计算方法与之相似。
2.5 姿态运动建模
当已知三轴稳定卫星的初始姿态以及本体系3 个轴的转动角速度,对姿态变化过程进行可视化建模和绘制时,就需通过数值积分计算变化过程各点的姿态信息。设卫星三轴转动的角速度矢量为。

此姿态角速度通常由安装在卫星上的陀螺仪进行测量,其输出值一般建立在惯性系下。
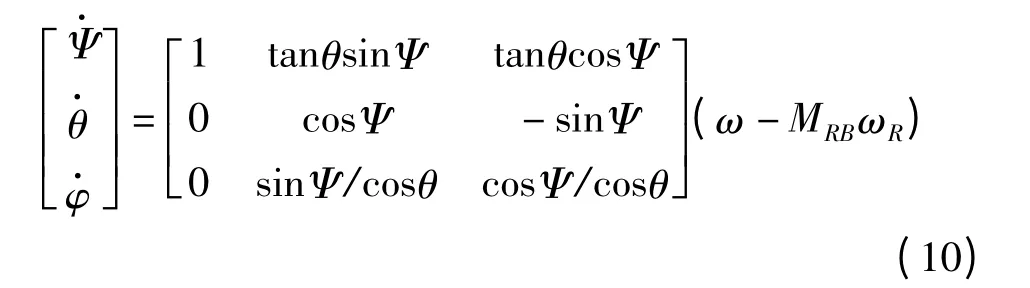
对于欧拉角姿态表示方式,3-2-1 转序下的姿态运动学方程为其中,MRB为参考系到本体系转换矩阵;ωR为参考系的转动角速度[12],据此式对各时间点进行积分求解即可。
需注意的是,欧拉角运动方程在θ=90°时存在奇点,这将给计算过程带来困难。
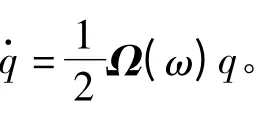
此运动方程无三角函数,不存在奇点问题,方程形式也较为简单,因而相比欧拉角姿态运动方程,其使用更为广泛。
3 应用效果
使用VC 编程工具及OpenGL 三维图形库进行了三轴稳定卫星飞行过程的可视化绘制,所实现的原型软件对姿态信息绘制效果如图1 和图2 所示。
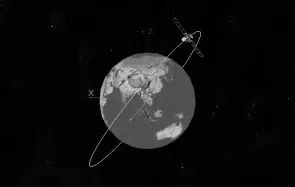
图1 卫星姿态的可视化效果
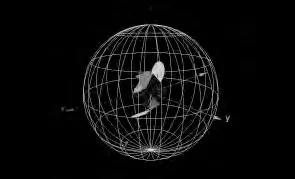
图2 姿态球绘制效果
4 结束语
本文对三轴稳定卫星姿态绘制与建模方法进行了系统地分析,给出了不同形式下的绘制方法,原型软件的绘制结果表明所给出的方法是可行的。由于三轴稳定卫星姿态信息有多种表达方式,根据卫星任务的特点,其姿态参考系选取也可能不同,具体可视化绘制中需灵活选用合适的绘制方法。
[1] 黄权,徐学军.基于OpenGL 的卫星跟踪仿真[J].计算机技术与发展,2007,17(2):131-134.
[2] 柴毅,史晶晶,冯大龙.基于Vega 的航天发射场视景仿真系统实现[J].计算机仿真,2007,24(6):62-65.
[3] 戴雪峰,金连文.基于OpenGL 实现的火箭弹道及卫星轨道三维可视化[J].测控技术,2006,25(1):17-19.
[4] 李英先,刘扬.基于STK 实现中继卫星业务运行可视化[J].信息与电子工程,2012,10(4):465-469.
[5] 张龙慧,宋杨,唐俊,等.基于OpenInventor 的卫星姿态控制可视化仿真[J].计算机技术与发展,2009,19(11):214-217.
[6] 郭伟民,赵新国,曹延华.基于STK 的微小卫星姿态控制可视化演示与验证[J].系统仿真学报,2008,20(增刊):319-322.
[7] HONG Geyao.The realization of flight simulation system based on openGL[C].2010 Second International Conference on Information Technology and Computer Science,2010:198-201.
[8] 章仁为.卫星轨道姿态动力学与控制[M].北京:北京航空航天大学出版社,1998.
[9] 徐波.OpenGL 编程指南[M].北京:机械工业出版社,2009.
[10]UJANG C A B C,TOOK C C,KAVCIC A,et al.A split quaternion nonlinear adaptive filter[C].IEEE International Conference on Acoustics,Speech,and Signal Processing,2009,5:1745-1748.
[11]SEBERRY J,FINLAYSON K,ADAMS S S.The theory of quaternion orthogonal designs[J].IEEE Transactions on Signal Processing,2008,56(1):256-265.
[12]刘林,胡松杰,王歆.航天动力学引论[M].南京:南京大学出版社,2006.

