层状非均质饱和土层波动响应研究
黄明汉,张卫平,张文忠
(1.天津大学 建筑工程学院,天津 300072;2.中交天津港湾工程研究院有限公司,中国交建海岸工程水动力重点实验室,天津 300222;3.大连理工大学海岸和近海工程国家重点实验室,辽宁 大连 116024)
在土层的地震反应研究中,多数研究将土介质简化为单相弹性介质,而不考虑土介质与其中流体间的相互耦合作用[1-2]。而随着近岸建筑以及海洋平台等工程的修建,考虑到结构物基础位于饱和沉积土层,饱和地层中地震波的传播情况与单相介质中情况有很大不同,简化的单相弹性介质波动理论难以准确描述两相饱和孔隙介质中波的传播现象。已有的研究资料表明,对沿海的软土地基中的地震剪切响应,由于孔隙水压对土的波动响应有很大影响,因此须把地基土处理成两相饱和介质以更接近于工程实际[3]。自Biot[4]建立了两相饱和多孔介质波动理论以来,许多学者应用该理论对饱和土中地震波传播特性做了很多相关研究[5-8],得到了许多有意义的结果。
本文根据Biot两相饱和土体动力耦合理论,通过建立饱和土层的动力刚度矩阵,对从基岩入射地震波作用下的饱和层状土层进行研究,对土体参数对波动响应的影响进行了详细数值研究。考虑到在实际工程实践中,基岩覆盖土层极少为理想均质土层,尤其是在海洋沉积性土层中土层分层比较明显,因此本文重点针对各种非均质土层下的波动响应的规律进行了对比分析,得出一些结论可供实际工程应用参考。
1 理论方程
1.1 理想饱和土介质运动控制方程
不计土颗粒的压缩性并将流体的黏性因素包含在动力渗透系数中,Zienkiewicz[9]等将Biot饱和土波动控制方程表示为:
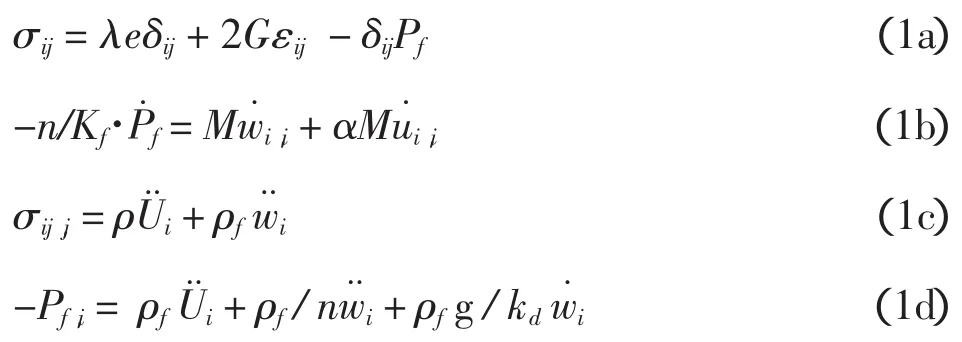
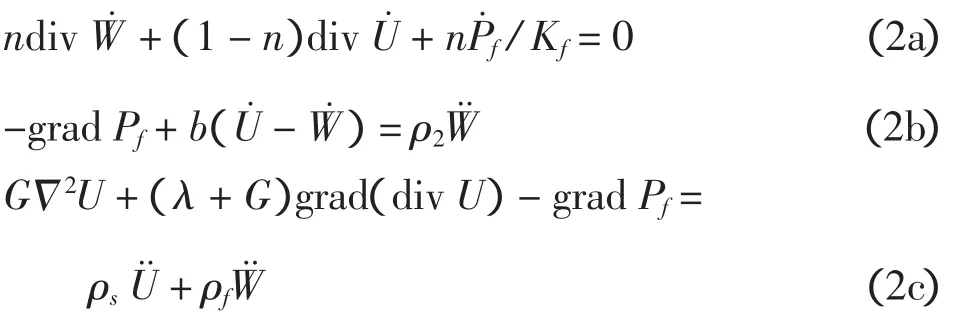
因此,由土骨架位移U和流体位移W表示的波动控制方程则可以写为:式中:σij为土体单元总应力;Pf为孔压;U和W分别为土骨架与空隙流体位移;w=n(W-U)为流体相对于土骨架的位移;n为饱和土孔隙率;kd为动力渗透系数;b=nρfg/kd为孔隙流体与土骨架间产生相对的内摩擦参数;ρ=(1-n)ρs+nρf为土体总密度,其中ρs和ρf分别为流体与土颗粒密度;λ,G为土骨架Lame常数;Kf为流体体积模量;δij为Kroneker函数;Δ2为Laplace算子。
1.2 饱和层状土层刚度矩阵的建立
作为分析层状场地的基本单元,在一个材料特性参数为常数的水平土层局部坐标系中,将z轴向下,坐标原点位于土层顶部。考虑到土体的黏滞性,计入土体阻尼比ζS的影响后,土介质中Lame常数以及波速等参数可改写成如下复数形式[7]:

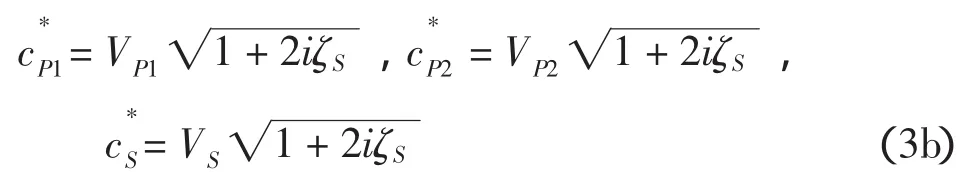
引入膨胀势函数 φ1,φ2,旋转势函数 ψ1,ψ2,φ1和ψ1为土骨架势函数,φ2和ψ2为孔隙流体势函数,土骨架及孔隙流体位移可表示为:

将上式代入控制方程(2),以势函数表示饱和介质中的波动方程,耦合方程组分别描述了饱和土中P波(包含P1波和P2波)及SV波的传播特征,考虑到介质中不同波的运动分量,饱和土层中平面波解的势函数通解可写为以下形式:

另一方面,由饱和介质中的本构关系可得到饱和土中应力及压强与位移的关系,通过两者之间的关系即可得到饱和土层的刚度矩阵关系方程。


2 数值计算分析
在本文饱和地基波动响应研究中,取饱和土层的力学相关参数参考Schnabel[10]等人在SHAKE91中算例,本文中取值如表1所示,计算模型如图1所示,在默认条件下,土层厚度d均取为10m,对于土介质剪切模量参数,本文以剪切波波速描述,对于剪切波波速土介质中取200m/s,基岩取2000m/s,土体阻尼比取0.05。对于地震波实例计算本文取Loma Prieta(1989)波,由基岩垂直入射,加速度时程曲线如图2所示。

表1 饱和土层的计算参数Table 1 parameters of saturated soil layers

图1 计算模型Fig.1 Sketch of calculation model

图2 基岩入射剪切波时程曲线Fig.2 The time curve of acceleration from bedrock
2.1 模型验证
当将饱和模型中流体密度ρf和孔隙率n以及水的体积模量Kf等参数取足够小时,本文模型即退化为单相弹性介质模型。为验证本文数值模型计算程序的正确性,将本文的饱和模型极限条件下计算结果与广泛使用的一维等效线性化土体地震反应分析程序SHAKE91[10]计算结果进行了对比,如图3所示,从两种不同方式取得的一维线性土体频域内的加速度放大系数可以看出,除在低频有较小差别外,其余频率条件下均能吻合较好,验证了本文饱和模型计算的正确性。

图3 本文模型取极限时与SHAKE91结果对比Fig.3 Comparison of results between This article′s ultimate solutions with SHAKE91
图4为本文饱和介质条件下与SHAKE91加速度放大系数的比较,通过两者的对比可以看出,除在低频时饱和模型计算结果相对单相介质稍微偏大以外,饱和模型下的计算结果与单相介质相比都有明显偏小趋势,由此可见,饱和介质中土骨架受到与流体部分的相互耦合作用能显著减小土层的振动响应。

图4 土层在饱和与单相下加速度放大系数对比Fig.4 Comparison of acceleration amplification between saturated soil with single-phase soil
2.2 均质条件下土层的波动响应
当层状土的各层土参数值相同时,则层状模型退化为均质模型。在实际地质环境中,基岩的埋层深度差异极大,且基岩面以上的覆盖土层力学特性也各不相同,本文为了研究不同基岩面上覆盖土层深度以及覆盖土层力学参数对剪切波波动的影响,在本文算例中选取土层深度分别为15m,30m,60m和150m四种埋深工况,而对土体基岩波速比则分别选取0.02,0.05,0.1三种工况条件进行了对比研究,其中基岩剪切波速固定取2000m/s。
从图5中不同埋深条件下土层加速度的放大系数可以看出随着基岩埋深的增大,土层的放大系数衰减明显,尤其是在150m基岩埋深工况条件下,加速度放大系数随着频率增大的衰减极为明显,在频率超过10 Hz后,基岩入射剪切波几乎不能到达地表处。从不同基岩埋深的加速度放大系数间的对比也可看出,随着埋深的增加,放大系数的共振峰值向低频转移,覆盖土层深度能显著阻碍高频波的传播。这种现象同样通过地表处加速度的时程曲线(图6)也可以看出,较高的基岩埋深能显著降低地表处的振动响应,尤其地震波中的高频成分被大大削弱,与图5频域内结果吻合。

图5 不同基岩埋深下地表加速度放大系数对比Fig.5 Comparison of acceleration amplification with different soil depth

图6 不同基岩埋深下地表加速度对比Fig.6 Surface acceleration curve with different soil depth
图7为在不同土层基岩波速比条件下土层的加速度放大系数反应曲线,在算例中通过了3种不同波速比下土层的波动响应,可以很明显看出当土层基岩波速比越小,也即是在土层基岩力学参数差别越大条件下,土层的波动响应也越小,并且高频下的衰减更加明显。同样通过时域实例的地表处加速度的时程曲线(图8)可以看出,较低的土层基岩波速比即更软的覆盖土层能显著降低地表处的振动响应,尤其地震波中的高频成分被削弱。

图7 不同土层基岩波速比下地表加速度放大系数对比Fig.7 Acceleration amplification with different soil-rock velocity ratio

图8 不同土层基岩波速比下地表加速度对比Fig.8 Surface acceleration curve with different soil-rock velocity ratio
2.3 非均质层状条件下土层的波动响应
在实际工程实践中,基岩覆盖土层极少为理想均质土层,尤其是在海洋沉积性土层中土层分层比较明显,不同层间的力学性质有较大不同。为了研究各类非均质土层在剪切波作用下的响应,本文对上软下硬、下硬上软、软夹层以及硬夹层土层分别进行了详细对比研究。
图9与图10分别为剪切波速随深度在不同变化趋势下的地表加速度频域与时域结果,在此数值算例中,分别对上软下硬 (V1∶V2∶V3=1∶1.1∶1.21)和上硬下软 (V1∶V2∶V3=1∶0.9∶0.81)土层进行了研究并与均质土层下计算结果进行了对比,从图9频域结果可以明显看出,在上软下硬土层条件下地表处波动响应要高于均质土层下结果,而在上硬下软土层条件下计算结果最小且共振峰向低频偏移,同样可从图10实际算例结果得到同样结论。

图9 不同土层分布下地表加速度放大系数对比Fig.9 Acceleration amplification with different layer types

图10 不同土层分布下地表加速度对比图Fig.10 Surface acceleration curve with different layer types
图11与图12分别为含有软夹层(Vm∶V0=0.2∶1)和硬夹层 (Vm∶V0=5∶1)条件下波动响应的频域与时域结果,从图12中对比结果可看出,均质土层下波动响应最大,含有硬夹层土层则偏小,而在含软夹层条件下,其地表加速度放大系数最大峰值仅有均质条件下1/3左右且随频域衰减最为显著。
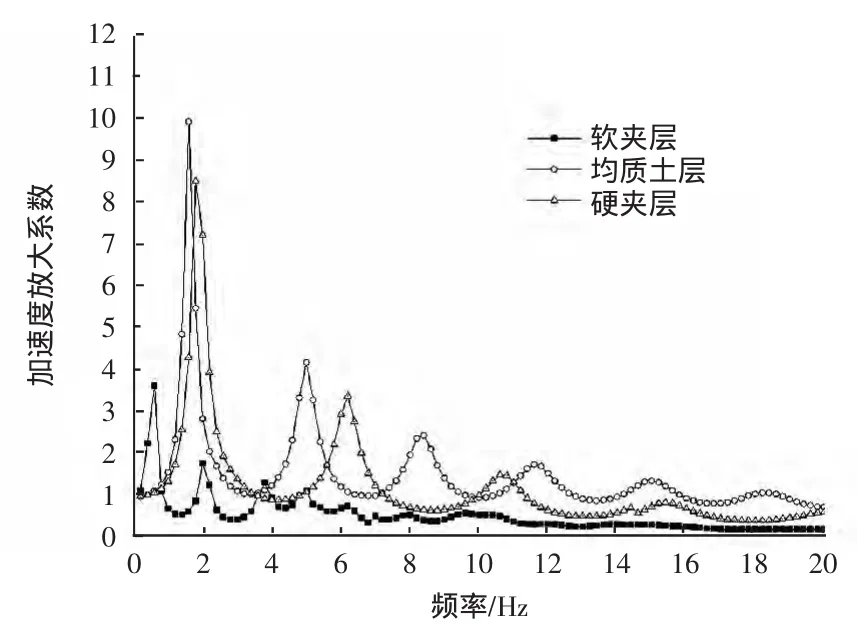
图11 含夹层条件下地表加速度放大系数对比Fig.11 Acceleration amplification with non-homogenous middle layer

图12 含夹层条件下地表加速度对比Fig.12 Surface acceleration curve with non-consistent middle layer
2.4 层状土层在地震剪切波作用下加速度幅值分布
为了进一步分析在地震波作用下加速度沿不同土层深度下的分布,本文分别以1 Hz,5 Hz,10Hz和15Hz频率为例,对各类土层下的加速度放大系数沿深度方向的分布进行了对比研究。从图13中不同土层间的对比可以看出,不同分布类型的土层有着不同的激发频率及分布形态,以均质土层为例,其在地表处的加速度放大系数在5 Hz时达到4.0以上,这与图11中此频率下存在共振峰结论吻合。从图中可以看出,在低频下除软夹层外土层中的不同深度处响应比较均匀且对基岩入射的地震波有放大作用,随着频率的升高,在土层沿深度方向呈现明显峰谷区,同样在含软夹层条件下,加速度分布呈现比较复杂形态,尤其可以看出,当地震波由下向上的传播过程中通过软夹层后被极大削弱,软夹层能有效阻止波的通过。而在含硬夹层的土层中,硬夹层中的波动分布则基本相同,显示出在波动响应中“刚性”的效果,在于上下层间的连接处有明显转折点。

图13 不同土层条件下加速度放大系数沿深度的分布曲线Fig.13 The distribution of acceleration amplification with different layer types
3 结语
本文通过对饱和复杂土层的动力刚度矩阵的建立,对基岩入射剪切波作用下的加速度放大系数以及在时域实例地震波作用下的波动响应进行了研究,并对加速度幅值沿深度方向的分布进行了详细的数值研究,得到如下结论。
1)通过对基岩垂直入射剪切波作用下的饱和土层与弹性单相土层的波动响应对比,在饱和条件下土骨架受到与流体部分的相互耦合作用能明显减小土层的振动响应。
2)随着埋深的增加,放大系数的共振峰值向低频偏移,覆盖土层深度能显著阻碍高频波的传播,较大的基岩埋深能吸收地震波的能量、显著降低地表处的振动响应,尤其是地震波中的高频成分被大大削弱。对于土层基岩波速比,当土层基岩波速比越小即上覆土层力学参数越低,土层地表处的波动响应也越小,并且高频下的衰减也更加明显。
3)在非均质上软下硬土层条件下地表处波动响应高于均质土层下结果,而相反在上硬下软土层条件下则能明显减小土层的波动响应。当土层中含有夹层时能显著降低地表处的波动响应,尤其在含软夹层条件下,其地表加速度放大系数最大峰值仅有均质条件下1/3左右且随波动频率迅速衰减。
[1] 高玉峰,金建新,谢康和,等.成层地基一维土层地震反应解析解[J].岩土工程学报,1999,21(4):498-500.GAO Yu-feng,JIN Jian-xin,XIE Kang-he,etal.General solution to the soil seismic response on stratified foundations[J].Chinese Journal of Geotechnical Engineering,1999,21(4):498-500.
[2] 蒋通,邢海灵.水平土层地震反应分析考虑频率相关性的等效线性化方法[J].岩土工程学报,2007,29(2):218-224.JIANG Tong,XING Hai-ling.An equivalent linear method considering frequency-dependent soil properties for seismic response analysis[J].Chinese Journal of Geotechnical Engineering,2007,29(2):218-224.
[3] JIN B,YUE ZQ,THAM LG.Stresses and excess pore pressure induced in saturated poroelastic half space by moving line load[J].Soil Dynamics and Earthquake Engineering,2004(24):25-33.
[4] BIOTM A.Generalized theory of acoustic propagation in porous dissipative media[J].Journal of Acoustic Society of America,1962(34):1254-1264.
[5] 杨峻,吴世明,蔡袁强,等.饱和土中弹性波的传播特性[J].振动工程学报,1996,9(2):128-137.YANG Jun,WU Shi-ming,CAI Yuan-qiang,etal.Characteristics of propagation of elastic waves in saturated soils[J].Journal of Vibration Engineeting,1996,9(2):128-137.
[6] 齐文浩,王振清,薄景山.土层非线性地震反应分析方法及其检验[J].哈尔滨工程大学学报 2010,31(4):444-450.QI Wen-hao,WANG Zhen-qing,BO Jing-shan.Development and verification of a method for analyzing the nonlinear seismic response of soil layers[J].Journal of Harbin Engineering University,2010,31(4):444-450.
[7] LIANG Jian-wen,YOU Hong-bing.Dynamic stiffness matrix of a poroelastic multi-layered site and its Green’s functions[J].Earthquake Engineering and Engineering Vibration,2004,3(2):273-282.
[8] 兰景岩,刘红帅,吕悦军.渤海土类动力非线性参数及合理性[J].哈尔滨工程大学学报,2012,33(9):1079-1085.LAN Jing-yan,LIU Hong-shuai,LV Yue-jun.Dynamic nonlinear parameters of soil in the Bohai Sea and their rationality[J].Journal of Harbin Engineering University,2012,33(9):1079-1085.
[9] ZIENKIEWWICZ O C,CHANG C T,BETTESS P.Drained,undrained,consolidating and dynamic behavior assumptions in soils[J].Geotechnique,1980(30):385-395.
[10] SCHNABELPB,LYSMER J,SEED H B.SHAKE:a computer program for earthquake response analysis of horizontally layered sites[C]//Report No.UCB/EERC-72/12,Earthquake engineering research center.Berkeley:University of California,1972:92.

