基于贝叶斯网络的驾驶疲劳程度识别模型
王连震,裴玉龙
(1.哈尔滨工业大学交通科学与工程学院,黑龙江哈尔滨150090;2.东北林业大学交通学院,黑龙江哈尔滨150040)
0 引言
随着汽车保有量的迅速增加,道路交通事故已成为当前世界各国面临的严重社会问题。据公安部统计,中国每年因道路交通事故死亡的人数约为7万人,其中因疲劳驾驶导致的死亡人数约占死亡总数的15%[1]。疲劳驾驶和酒后驾驶是交通事故的主要隐患,不同的是,酒后驾驶很容易被检测出来,而驾驶人的疲劳程度则不能被直接观测。因此,研究驾驶疲劳程度的识别和检测方法,可以有效预防疲劳驾驶,从而减少由其引发的道路交通事故、提高道路交通安全水平。
疲劳驾驶程度识别的相关研究引起了国内外学者的广泛关注。文献[2]将驾驶疲劳的检测方法概括为主观评定法(驾驶人陈述或填表)、生理指标测定法(分析脑电、心电、肌电、呼吸速率、血压等)和操控性能评定法(监测驾驶人对方向盘、刹车、档位的实际操作结果)。文献[3]以心率变异性为检测指标,采用人工神经网络分析方法对疲劳驾驶进行检测,精度可达90%。文献[4]采用脑电指标和心电指标对驾驶人在模拟驾驶过程中的心理疲劳状况进行测定,结果表明这两类指标能够较好地表征驾驶人的心理疲劳。文献[5]以方向盘转角的均值和标准差及车辆横向位置的标准差作为表征指标,验证了长时间驾驶、环境单调和困倦状态对驾驶人驾驶行为表现的负面影响。文献[6]提出通过采集车辆转向角信号的方法识别疲劳驾驶。文献[7]选取车速变化、油门、刹车、离合变化等驾驶行为数据作为驾驶人疲劳程度识别的指标。文献[8]以方向盘转动程度、车道偏离程度及驾驶人疲劳特征等作为评价指标,建立基于多通道信息融合的驾驶疲劳行为判定模型,提高了疲劳驾驶行为检测的精度。
文献[9]采用AdaBoost算法分类器,对自然光条件下驾驶人的眼睛状态进行识别,通过计算单位时间内眼睛闭合时间所占的百分比(Percentage of Eyelid Closure over the Pupil over Time,PERCLOS)指标来判断驾驶人疲劳程度。文献[10]采用闭眼总持续时间、时段内眨眼次数和眨眼时间均值等眼部行为特征作为表征疲劳程度的指标。文献[11]利用眼睛和嘴巴在驾驶过程中的特征作为参数判断驾驶人的疲劳程度。
文献[12]通过分析连续驾驶时间对驾驶特性指标(深度知觉差异、速度知觉差异、选择反应时间等)的影响,来判断驾驶人的疲劳程度。文献[13]以反应时间、脑电、驾驶行为等指标为参照,通过实验证明了卡罗林斯卡(Karolinska)睡眠量表与上述指标具有较高的相关性,可以作为检测驾驶人疲劳程度的替代方法。文献[14]设计开发了一种新的综合性调查表,不仅对驾驶人的自觉疲劳症状进行评定,而且对交通环境等影响因素进行感官定性测量,分析各种因素对驾驶疲劳的影响。文献[15]以PERCLOS值、连续驾驶时间、方向盘动作状态及方向变化与驾驶人反应不一致的情况等作为检测指标,采用TS模糊神经网络方法进行多目标信息融合,检测驾驶疲劳。
综上所述,国内外学者在驾驶疲劳度量指标及其测定方面已取得较为丰富的研究成果。但是,在驾驶疲劳程度识别方面,学者们大多采用单一类型指标进行判断。受仪器设备、驾驶习惯及周围环境等影响,单一指标在检测时通常呈现出不稳定性,已有部分学者开始利用综合指标对驾驶疲劳进行判断。本文通过贝叶斯网络模型在信息融合和概率推理方面的优势,对驾驶疲劳程度进行识别,以提高驾驶疲劳检测的准确性和可靠性。
1 基于贝叶斯网络模型的驾驶疲劳程度识别
驾驶疲劳作为一个不可直接观测的研究对象,其影响因素非常多且难以定量,各类度量指标对驾驶疲劳的界定又没有统一的标准。因此,判断驾驶疲劳程度是一个非常复杂的系统问题。与酒后驾驶的检测指标不同,所有用来检测驾驶疲劳的指标在获取过程中均会受到不同程度的干扰。目前,还没有一种方法能够对驾驶疲劳程度进行准确无误的检测。因此,使用概率论的方法对驾驶疲劳程度进行识别具有一定的合理性。
贝叶斯网络模型的基本思想是:在信息不完备的情况下,通过可观察随机变量(证据变量)推断不可观察随机变量(隐含变量),进行概率推理。利用贝叶斯网络求解驾驶疲劳程度识别的问题可以表述为:在已知疲劳度量指标测定结果的情况下,利用贝叶斯网络方法求解在一定影响因素条件下,疲劳状态处于各种程度(清醒、轻度疲劳、重度疲劳)时的概率。
驾驶疲劳贝叶斯网络的构建包括两个主要内容:1)确定网络节点;2)计算节点间的先验概率。其中,网络节点的选择取决于疲劳的各种特征及影响因素,而节点先验概率的确定则依赖于某个特征或因素对判断疲劳程度的可能性。
2 驾驶疲劳程度识别模型
2.1 驾驶疲劳贝叶斯网络结构
驾驶疲劳作为系统的核心,其复杂的影响因素即该系统的输入,在生理、眼动及驾驶绩效等方面表现出来的特征即该系统的输出。
将驾驶疲劳的影响因素分为三类:驾驶环境属性、驾驶人个体属性以及原始疲劳属性。各类影响因素的具体度量指标见图1。其中,温度、天气等变量是驾驶环境变量的父节点,相应的驾驶环境变量是温度、天气等变量的子节点,以此类推。驾驶疲劳贝叶斯网络结构的输入层用变量I表示,其中驾驶环境属性用I1表示,驾驶人个体属性用I2表示,原始疲劳属性用I3表示。imn表示第m个输入层变量的第n种状态。输入层节点各个变量的状态分类见表1~表3。
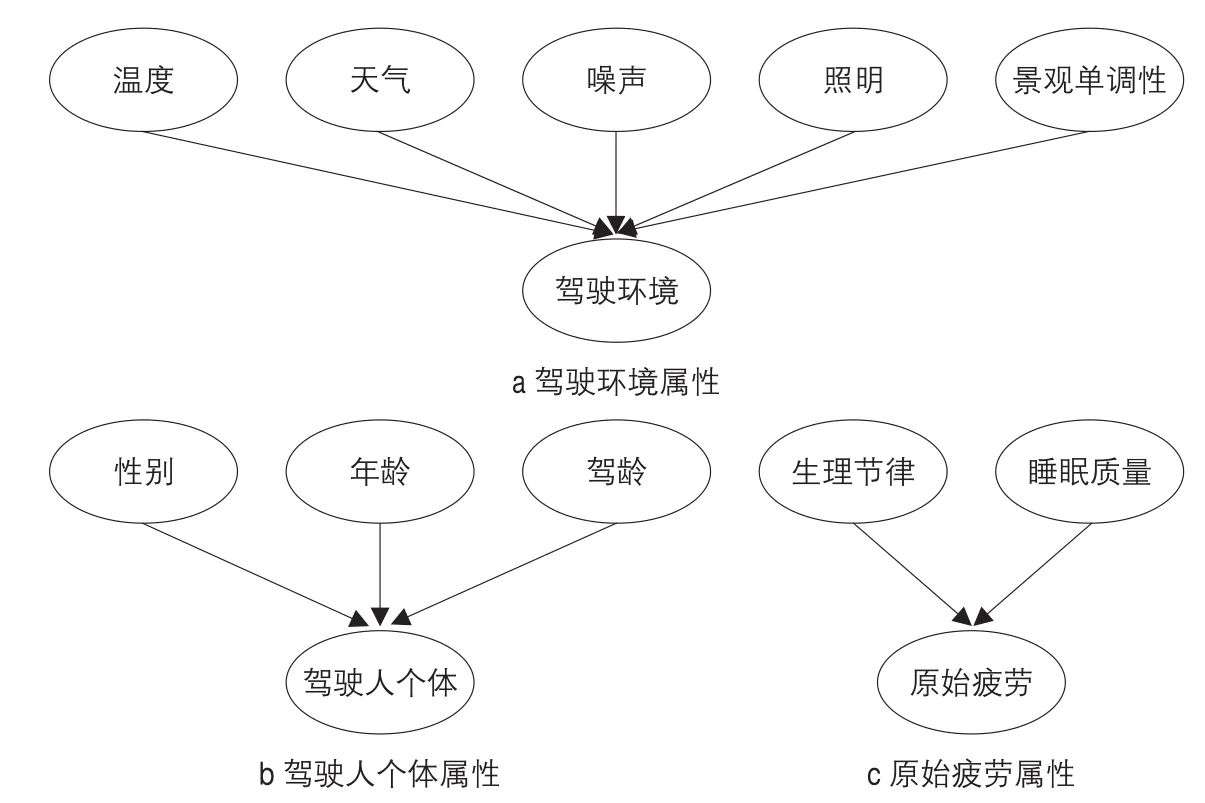
图1 驾驶疲劳影响因素Fig.1 Influencing factors of driving fatigue

表1 驾驶环境属性及其父节点变量状态分类Tab.1 Driving environmental attribute and classification of its father nodes variable

表2 驾驶人个体属性及其父节点变量状态分类Tab.2 Drivers’individual attribute and classification of its father nodes variable

表3 原始疲劳属性及其父节点变量状态分类Tab.3 Original fatigue attribute and classification of its father nodes variable
目前,驾驶疲劳的检测方法可归纳为生理指标检测(如脑电、心电等)、面部特征指标检测(如眼动指标)、驾驶绩效指标检测等,且均已形成较为成熟的检测手段。由于驾驶疲劳程度的表征指标众多,本文采用皮尔逊相关系数法对各类指标之间的相关性进行分析。结果发现:脑电指标中,θ波与β波在各个时段出现频率的比值θ/β与其他指标的相关性最好;心电指标中RR间期(一次心跳的周期)的标准差,即24 h心率变异性参数(Standard Deviation of NN Intervals,SDNN)与其他各类指标的相关性最好;眼动指标中PERCLOS与其他各类指标的相关程度最高;驾驶绩效指标中速度标准差(Standard Deviation of Speed,SDS)与其他各类指标的相关性最高。
因此,选择脑电指标θ/β、心电指标SDNN、眼动指标PERCLOS、驾驶绩效指标SDS作为驾驶疲劳贝叶斯网络的输出层变量,用O表示,见表4。Oqj表示第q个输出层变量的第j种状态。采用K均值聚类分析法对各个度量指标进行分类研究,各个指标的状态分类及阈值见表5~表8。
疲劳程度作为隐含层变量,用H表示,变量的取值用hk表示,其中k=1,2,3,分别表示驾驶疲劳的三种状态类型:清醒、轻度疲劳、重度疲劳。
当贝叶斯网络的输入层、隐含层及输出层确定后,驾驶疲劳贝叶斯网络结构即可确定。图2为某一时刻t,当贝叶斯网络中各个节点变量的状态一定时,所有节点构成的网络结构即驾驶疲劳静态贝叶斯网络结构。其中,驾驶环境变量是驾驶疲劳变量的父节点,相应的驾驶疲劳变量是驾驶环境变量的子节点,以此类推。随着驾驶时间的推移,网络节点中某些变量的状态势必会发生变化。根据贝叶斯理论,这种变化是由上一时刻和当前时刻网络中各个节点的状态所决定的。由所有时刻的静态贝叶斯网络按时间顺序展开,形成驾驶疲劳动态贝叶斯网络结构,见图3。
2.2 贝叶斯网络条件概率表的确定
在建立的驾驶疲劳贝叶斯网络模型中,条件概率分为两类:一类是输入层变量与隐含层变量之间的条件概率,另一类是隐含层变量与输出层变量之间的条件概率。
1)第一类条件概率。
首先通过统计分析疲劳驾驶交通事故数据和问卷调查结果得到父节点的先验概率及父节点与其子节点的条件概率,然后计算所有节点的条件概率分布,计算公式见式(1)和式(2)。输入层变量与隐含层变量间的条件概率计算结果见表9。
由贝叶斯公式推导可得

将式(1)的计算结果进行归一化处理可得

式中:Hk,Hl为变量H的第k,l种状态,对驾驶疲劳这个变量而言,l的取值为1,2,3,分别表示驾驶疲劳的三种状态类型,即清醒、轻度疲劳、重度疲劳;Ix为变量H的第x个父节点,Ix之间相互独立;N为变量I的个数;M为变量H状态分类的个数,对驾驶疲劳而言,M=3。
2)第二类条件概率。
通过分析实验数据获得。每个指标与隐含层之间的条件概率计算公式见式(3)。驾驶疲劳程度与输出层变量间的条件概率计算结果见表10。

式中:P(Or|Hk)为疲劳程度为Hk、度量指标取值为Or的概率;Nr为第r个度量指标取值为Or的样本数量;Na为总样本数量。
2.3 驾驶疲劳程度贝叶斯网络识别模型
输入层变量和输出层变量统称为贝叶斯网络中的证据变量。利用贝叶斯网络建立驾驶疲劳程度识别模型的原理是在已知网络中各节点先验概率的前提下,结合证据变量的取值,根据贝叶斯公式计算不同驾驶疲劳程度的后验概率。
假设It,Ht,Ot分别表示驾驶疲劳程度贝叶斯网络中的输入层变量、隐含层变量、输出层变量在t时刻的状态。输入层和输出层各变量之间均满足条件独立性假设,即输入层或输出层中任一变量取值的概率与其他变量的取值无关。
由贝叶斯公式可得

式中:P(Hk|I,O)为输入、输出层变量状态一定时,隐含层变量为Hk的概率;P(Hk)为隐含层变量状态为Hk时的全概率;P(I,O|Hk)为隐含层变量状态为Hk时,输入、输出层变量取一定状态时的概率;P(I,O)为输入、输出层变量取一定状态时的全概率。

表4 驾驶疲劳度量指标Tab.4 Measure index of driving fatigue

表5 脑电指标状态分类及取值Tab.5θ/β index classification and value

表6 心电指标状态分类及取值Tab.6 SDNN index classification and value

表7 眼动指标状态分类及取值Tab.7 PERCLOS index classification and value

表8 驾驶绩效指标状态分类及取值Tab.8 SDS index classification and value
由变量间的条件独立性假设可得

由全概率公式可得
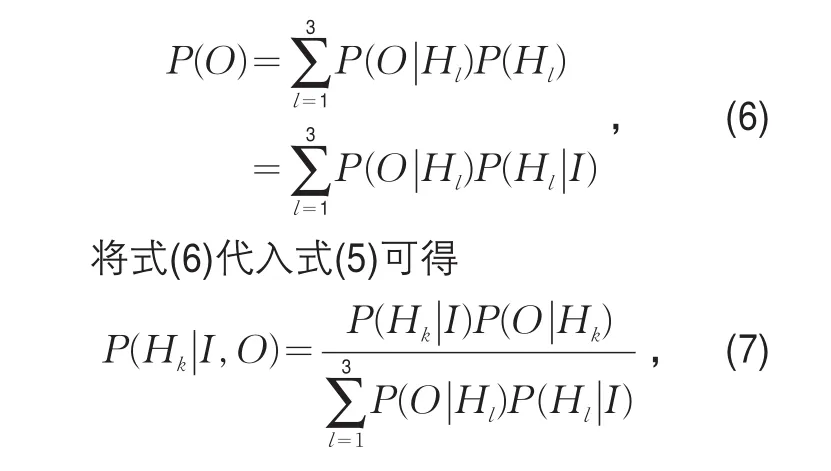
式中:P(Hk|I)为输入层变量状态为I、隐含层变量状态为Hk的概率;P(O|Hk)为隐含层变量状态为Hk、输出层变量状态为O的概率。
由变量间的条件独立性假设和全概率公式可得
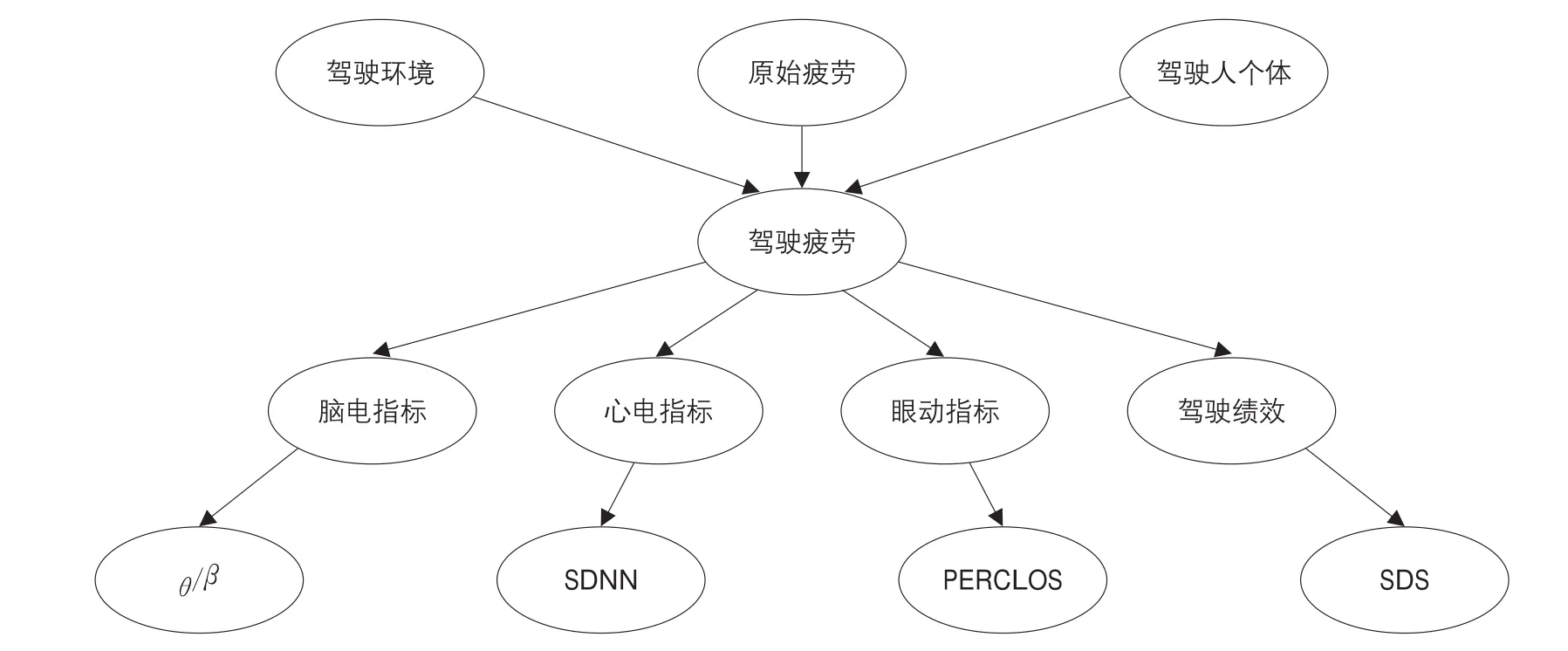
图2 驾驶疲劳静态贝叶斯网络结构Fig.2 Static Bayesian Network structure of driving fatigue

图3 驾驶疲劳动态贝叶斯网络结构Fig.3 Dynamic Bayesian Network structure of driving fatigue

式中:m,n,q分别为三个输入层变量状态的不同类型。联立式(7)、式(8)和式(9)可得到基于静态贝叶斯网络的驾驶疲劳程度识别模型。根据动态贝叶斯理论,t时刻的驾驶疲劳程度只与t时刻的输入层变量状态It和t-1时刻的疲劳程度有关,而与其他时刻的属性集状态无关,因此

式中:t=1,2,…,T;k=1,2,3;r=1,2,3,4;v=1,2,3,表示驾驶疲劳的三种状态类型;T为时刻t的个数。联立式(7)、式(10)和式(11)可得到基于动态贝叶斯网络的驾驶疲劳程度识别模型。

3 模型有效性验证
采用模拟驾驶的方法进行实验设计。实验设备包括模拟驾驶仿真实验平台——AS1300卡车驾驶模拟系统、多通道生物生理记录仪、摄像机等。同时采用斯坦福嗜睡量表(Stanford Sleepiness Scale,SSS)对驾驶人的主观疲劳状况进行问卷调查,以了解驾驶过程中驾驶人对疲劳的主观感受。
共有4名实验对象,其中男性驾驶人2名,女性驾驶人2名,平均年龄33.2岁,驾龄均在1年以上。所有实验对象均身体健康,无慢性疾病或生理缺陷。实验开始前一天睡眠质量均良好,无不良情绪,且实验前24 h内无饮酒或服用药物情况。
本次模拟驾驶的实验场景是平原高速公路,试验线路为近似矩形的环状道路,线路全长200 km,交通条件为自由流,行驶速度依照每个实验对象的驾驶习惯自行设定。在正式实验之前,需要对实验对象进行模拟驾驶培训和实验设备的操作训练,要求所有实验对象在正式实验时能熟练操作各种设备。实验开始前,对实验对象进行主观疲劳问卷调查并记录,还要在静坐状态下使用生物生理记录仪测试每个实验对象的脑电和心电指标,并用摄像机记录眼动情况,测试时间为5 min。正式实验过程中,使用生物生理记录仪、摄像机连续测试并记录驾驶人的脑电、心电、眼动、行驶速度等指标数据,每隔30 min进行主观疲劳问卷调查。驾驶任务结束后,立即重复进行上述测试过程。

表9 疲劳程度与输入层变量间的条件概率Tab.9 Contingent probability of fatigue degree and variables of input layer
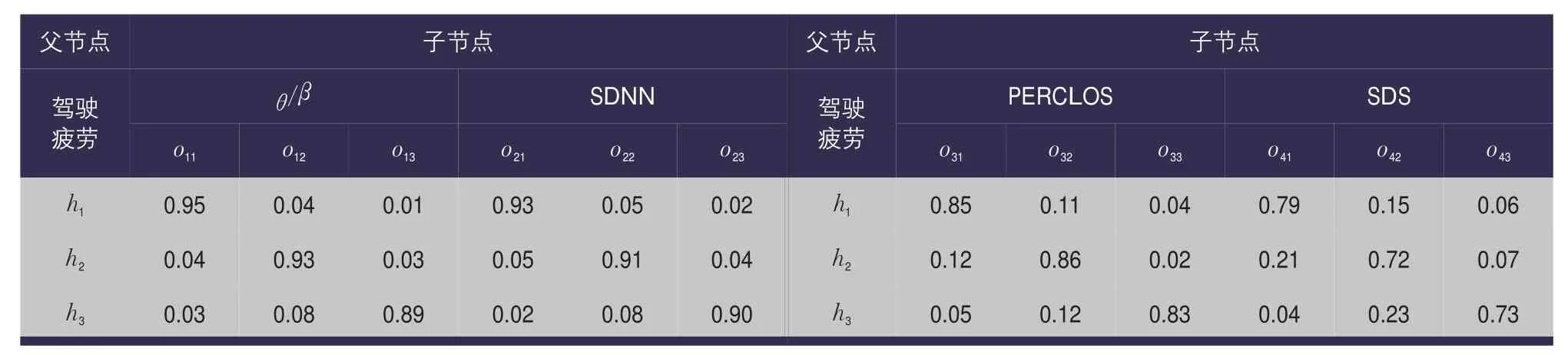
表10 疲劳程度与输出层变量间的条件概率Tab.10 Contingent probability of fatigue degree and variables of output layer

图4 基于贝叶斯网络的驾驶疲劳程度识别流程Fig.4 Driving fatigue recognition flow based on Bayesian Network
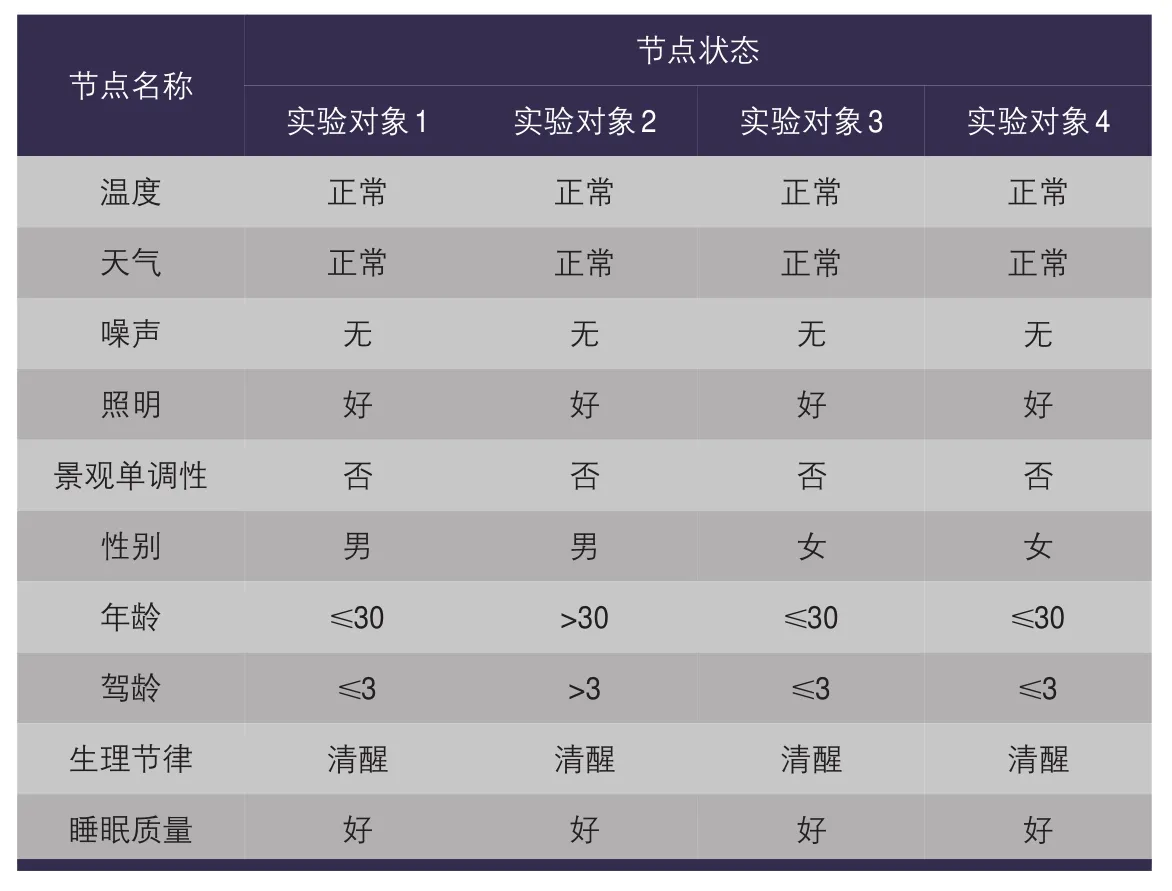
表11 初始时刻父节点变量状态Tab.11 Variable state of root nodes at initial moment
利用贝叶斯网络模型对疲劳程度进行识别的流程见图4。
根据实验设定的条件和实验对象的特征,确定初始时刻父节点变量的状态,见表11。根据父节点变量的状态,可以获得驾驶环境属性、驾驶人个体属性和原始疲劳属性3个输入层节点的先验概率。根据驾驶疲劳贝叶斯网络模型的计算结果,取最大概率对应的状态为该时刻驾驶疲劳的识别状态。
根据实验测定的指标数据,确定输出层节点变量的状态。以实验对象1为例,应用本文建立的模型对各个时刻该对象的疲劳程度进行判断。初始时刻测得实验对象1的脑电指标、心电指标、眼动指标、驾驶绩效指标的状态均为“正常”。因此,各节点该状态的概率即为1,其他状态概率均为0。确定各个节点的状态和先验概率后,应用静态贝叶斯网络模型可以得到驾驶疲劳在初始时刻不同状态时的条件概率。
将初始时刻不同驾驶疲劳程度的概率作为已知条件,利用动态贝叶斯网络模型,计算下一时刻不同驾驶疲劳程度的概率,以此类推,即可得到所有时刻不同驾驶疲劳程度的概率。实验对象1的不同驾驶疲劳程度随驾驶时间的变化情况见图5。同理,可获得其余3名实验对象在各个时刻不同疲劳程度的概率,结果见表12。
由图5可知,随着驾驶时间的增加,驾驶人保持清醒状态的概率不断降低,保持轻度疲劳状态的概率呈现出先增加后降低的趋势,而保持重度疲劳的概率在开始阶段处于较低的水平,随着清醒和轻度疲劳状态概率水平的降低,重度疲劳状态的概率水平不断增加。
利用SSS方法采集驾驶人主观疲劳评价数据,对采集到的108个疲劳程度样本进行判断,其中“清醒”程度的样本数量为43个,“轻度疲劳”程度的样本数量为45个,“重度疲劳”程度的样本数量为20个。分别采用单一指标以及本文建立的贝叶斯网络模型对驾驶人的疲劳程度进行判断,并与主观疲劳测评结果进行对比,结果见表13。
由表13可知,利用本文建立的贝叶斯网络模型与主观疲劳量表对驾驶疲劳累积程度进行对比判断时,准确率可达92.9%,而采用单一指标进行判断时,准确率均低于本文建立的模型。说明基于贝叶斯网络的驾驶疲劳程度识别模型不仅能消除单一指标失效时产生的误判和漏判,并且具有较高的准确性。因此,该模型在识别驾驶疲劳累积程度方面具有较高的可信度。
4 结语
本文以贝叶斯理论为研究基础,针对单一指标在检测驾驶疲劳程度中的不足,提出融合驾驶疲劳多种度量指标和影响因素等信息的驾驶疲劳程度贝叶斯网络识别模型。通过模拟驾驶实验采集驾驶疲劳度量指标数据,分别以脑电指标、心电指标、眼动指标和驾驶绩效指标等单一指标和贝叶斯网络模型对驾驶疲劳程度进行判断,并与主观疲劳评价结果进行对照。结果表明,应用贝叶斯网络模型进行驾驶疲劳程度识别不仅能消除单一指标失效时产生的误判和漏判,而且可以提高识别的准确性。
模型中条件概率的确定基于事故数据、问卷调查结果和实验数据,受主观因素和样本数量的影响较大,后续研究中应进一步完善条件概率的确定方法,以提高模型精度。

图5 实验对象1不同驾驶疲劳程度随驾驶时间的变化Fig.5 Change of experimental object I in driving fatigue degree along with driving time

表13 单一指标和贝叶斯模型对驾驶疲劳程度的识别结果Tab.13 Driving fatigue recognition results of single index and Bayesian model
[1]袁翔,黄博学,夏晶晶.疲劳驾驶检测方法研究现状[J].公路与汽运,2007,18(3):51-54.Yuan Xiang,Huang Boxue,Xia Jingjing.Research Status of Fatigue Driving Detecting Methods[J]. Highways and Automotive Applications,2007,18(3):51-54.
[2]Lal S K L,Craiga Ashley.A Critical Review of the Psychophysiology of Driver Fatigue[J].Biological Psychology,2001,55(3):173-194.
[3]Patel M,Lal S K L,Kavanagha D,Rossiterb P.Applying Neural Network Analysis on Heart Rate Variability Data to Assess Driver Fatigue[J].Expert Systems with Applications,2011,38(6):7235-7242.
[4]Zhao Chunlin,Zhao Min,Liu Jianpin,et al.Electroencephalogram and Electrocardiograph Assessment of Mental Fatigue in a Driving Simulator[J].Accident Analysis and Prevention,2012(45):83-90.
[5]Riccardo Rossi,Massimiliano Gastaldi,Gregorio Gecchele.Analysis of Driver Task-related Fatigue Using Driving Simulator Experiments[J].Procedia-Social and Behavioral Sciences,2011(20):666-675.
[6]Takei Y,Furukawa Y.Estimate of Driver’s Fatigue through Steering Motion[C]//IEEE.2005 IEEE InternationalConference On System,Man and Cybernetics.New York:IEEE Conference Publications,2005:1765-1770.
[7]张晖.基于驾驶行为的疲劳程度识别研究[D].武汉:武汉理工大学,2009.Zhang Hui.Research on Driving Fatigue Recognition Based on Driving Behavior[D].Wuhan:Wuhan University of Technology,2009.
[8]秦洪懋,刘志强,汪澎.基于多通道信息融合的疲劳驾驶行为分析研究[J].中国安全科学学报,2011,21(2):115-120.Qin Hongmao,Liu Zhiqiang,Wang Peng.Research on Drowsy Driving Behavior Based on Multi-channel Information Fusion[J].China Safety Science Journal,2011,21(2):115-120.
[9]Wu Qing,Sun Bingxi,Xie Bin,Zhao Junjie.A PERCLOS-based Driver Fatigue Recognition Application forSmartVehicle Space[C]//IEEE.Third InternationalSymposium on Information Processing.New York:IEEE,2010:437-441.
[10]潘晓东,李君羡,徐小冬.基于眼部行为的驾驶疲劳评价指标的阈值[J].同济大学学报(自然科学版),2011,39(12):1811-1815.Pan Xiaodong,Li Junxian,Xu Xiaodong.Threshold Value of Indices of Eye States to Monitor Driving Fatigue[J].Journalof Tongji University(Natural Science),2011,39(12):1811-1815.
[11]张建明,魏林峰,刘志强,汪澎.基于贝叶斯网络的疲劳度及注意力检测[J].计算机工程,2012,38(9):189-192.Zhang Jianming,Wei Linfeng,Liu Zhiqiang,Wang Peng.Fatigue and Attention Detection Based on Bayesian Network[J].Computer Engineering,2012,38(9):189-192.
[12]马艳丽,裴玉龙.连续驾驶时间对驾驶特性测评指标的影响[J].中国公路学报,2009,22(1):84-88.Ma Yanli, Pei Yulong. Influences of Continuous Driving Time on Test Indicators of Driving Characteristics[J].China Journal of Highway and Transport,2009,22(1):84-88.
[13]Kaida K,Takahashi M,Akerstedt T,et al.Validation ofthe Karolinska Sleepiness Scale against Performance and EEG Variables[J].Clinical Neurophysiology,2006,117(7):1574-1581.
[14]舒红宇,李发权,易树平,藤本英昭,上野義雪.汽车驾驶疲劳的一种综合性评定方法[J].上海交通大学学报,2008,42(8):1338-1343.Shu Hongyu,LiFaquan,YiShuping,HideakiFujimoto,YoshiyukiUeno.A Comprehensive Evaluation Method for Automotive Driving Fatigue[J].Journal of Shanghai Jiaotong University,2008,42(8):1338-1343.
[15]沈永增,胡立芳,冯继妙.多源信息融合在驾驶疲劳检测中的应用[J].计算机应用与软件,2012,29(2):272-275.Shen Yongzeng,Hu Lifang,Feng Jimiao.Multi-source Information Fusion Application to Driving Fatigue Detection[J].Computer Applications and Software,2012,29(2):272-275.

