基于相关性分析的PCBA热力学模型修正
王开山,李传日,郭恒晖,庞月婵,李鹏
(北京航空航天大学可靠性与系统工程学院,北京100083)
基于相关性分析的PCBA热力学模型修正
王开山,李传日,郭恒晖,庞月婵,李鹏
(北京航空航天大学可靠性与系统工程学院,北京100083)
目的精确且高效地对印制电路板组件热力学模型进行修正。方法采用基于拉丁超立方抽样试验设计和Speraman等级相关系数计算公式的相关性分析方法,找出电子产品热仿真试验中对元器件表面温度值影响较大的输入参数,然后进一步分析得出输入与输出之间的函数关系。在此基础上给出印制电路板组件(PCBA)热力学模型修正的一般方法流程。最后利用该方法对某航空电子产品中一块PCBA的热力学模型进行修正。结果修正结果较精确且只调用2次有限元软件。结论该热模型修正方法具有较高的精确性和高效性,可推广用于工程实践。
拉丁超立方抽样;Speraman等级相关系数;参数筛选;热模型修正
热仿真分析计算是电子产品可靠性虚拟试验中获取热应力剖面的重要途径,工程上为了提高效率,在建立产品的热分析模型时往往会对产品的真实模型进行许多简化和假设。同时作为产品热模型输入条件的很多参数,如几何尺寸、装配接触关系、材料属性(导热系数)、热载荷(内部生成热或功率)、边界条件(对流传热膜系数、辐射系数)、环境温度等都存在着一定程度的不确定性[1]。这些因素会使仿真计算所得到的温度值与产品热测量试验温度之间存在着偏差,有时这种偏差会超过可接受的范围。因此,为了减小仿真偏差,提高模型精度从而为故障预计提供更精确的热应力剖面,必须对产品热模型进行修正。
目前,工程上普遍采用基于设计经验的试凑法进行热模型修正,即直接依据经验对热模型偏差处的参数进行感性调整和试算。由于该方法每次试算需要调用有限元软件进行解算,因而需要很大的人力和时间投入,效率不高,并且要调整哪些参数全凭经验和感性认识,并没有理论依据。另外,工程上通常把偏差限制在10%之内作为模型修正的目标,而不是寻求最优目标值,因此精度很低。
综上所述,传统的试凑法已经不能满足热模型修正的需要,而且目前对热模型修正的研究尚处空白。为了提高热模型修正的精度和修正效率,研究新的热模型修正方法十分必要。文中利用相关性分析方法结合一个简单的PCBA模型分析了热仿真输入输出之间的相互关系,然后利用得出的结论给出了热模型修正的方法流程,并对一个真实产品的PCBA案例进行了热模型修正,以说明该方法的可行性。
1 热仿真输入输出关系分析
首先,结合一个简单的PCBA模型对热仿真输入输出关系进行分析,该PCBA的CAD模型如图1所示。该分析对象包括1个PCB板,2个元器件,较小的为C1,较大的为C2。
1.1 输入输出参数筛选
在可靠性仿真试验中,热仿真分析的目的主要是获取器件表面上的温度以作为后期故障预计的应力输入之一,因此输出参数应选择器件表面温度。这里以C1表面上的温度值作为输出参数进行分析。

图1 分析对象的CAD模型Fig.1 The CAD model of the analysis object
对于输入参数,影响C1表面温度的参数有PCBA各部件的几何尺寸、装配接触关系、材料属性(导热系数)、热载荷(内部生成热或功率)、边界条件(对流传热膜系数、辐射系数)和环境温度等。PCB和器件的材料参数会因生产工艺、铺层、电路通孔分布等的不同而表现出较大的波动性和各向异性[2—5]。另外器件在实际工作中往往不会在额定功率固定值上工作,而是在额定功率值附近呈现一定的波动性。这两方面的因素可能是造成热仿真值与热测量值之间出现偏差的主要原因,因此这里将C1,C2和PCB各自3个轴向的导热系数及各自的内部生成热(器件内部生成热等于器件功率与器件体积的比值)作为初始筛选输入参数,即:C1-IH,C2-IH,PIH,C-TCx,C-TCy,C-TCz,P-TCx,P-TCy和P-TCz。几何尺寸及装配接触关系在建模时可以控制,不考虑其波动性。另外,热测量试验中的边界条件和环境温度可以得到很好的控制,在此也不考虑其波动性。
1.2 相关性分析
初始筛选出来的9个参数均具有波动性较大的特点,但并不是所有参数都会对输出参数(即C1表面温度)产生较大影响,因此需要定量的相关性分析筛选出对C1表面温度影响较大的参数。首先确定每个初始筛选参数的取值范围,上下限值一般偏离初始仿真参数值的5%左右,也可根据工程经验对个别参数进行增大或减小的调整。本案列PCBA各初始筛选参数取值的上下限见表1。
利用拉丁超立方方法对每个参数在各自取值范围内进行抽样,抽取15个参数组合并对每组参数组合进行仿真计算得到每组参数对应的C1表面温度值,这15个样本点见表2。拉丁超立方抽样是一种多维分层抽样方法,该方法可以在整个设计空间中高效无重复抽取样本,能够以较少的试验样本获取较高的计算精度[6—7]。

表1 初始筛选参数上下限值Table 1 The upper and lower limit values of the initial screening parameters

表2 拉丁超立方抽样样本点Table 2 The sample points of Latin hypercube sampling
按照公式(1)所示的Speraman等级相关系数计算公式计算各参数与C1表面温度的相关系数,计算结果见表3。

式中:R(xi)表示将不确定参数的抽样值(x1,x2,…,xn)按升序或降序排列时xi的排序号;R(yi)表示将相应的响应计算值(y1,y2,…,yn)按升序或降序排列时yi的排序号;n表示抽样次数。其中,若|rp|≤0.3,表示相关关系很弱;0.3<|rp|≤0.5,属于低相关;0.5<|rp|≤0.8,属于中度相关;0.8<|rp|≤1属高度相关。因此,可通过rp判断出不确定参数对结构特征量的影响程度,完成参数对输出量相关性的分析。文中把低相关及以上(即|rp|>0.3)的参数确定为最终待修正参数,低相关以下(即|rp|≤ 0.3)的参数排除不予考虑[8—11]。
从相关性系数计算结果中可以看出,只有1号元器件的内部生成热C1-IH与输出响应即1号元器件表面温度T-C1的相关系数大于 0.3,为0.9073;其余参数与输出响应的相关性系数均小于0.3,因而可以得出结论:元器件自身的内部生成热(或者说功率)是影响其表面温度的最重要因素,其导热系数、周围器件的内部生成热和导热系数、PCB的导热系数及内部生成热均对其表面温度影响很小。
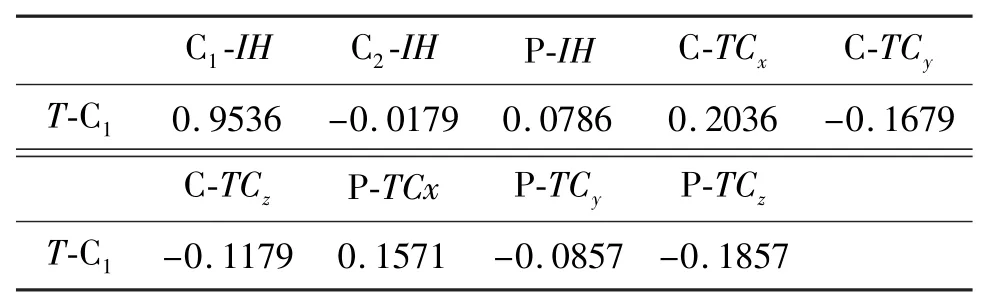
表3 相关系数计算结果Table 3 The calculation results of correlation coefficient
1.3 函数关系拟合
在得出器件表面温度只与自身内部生成热关系较大这一结论之后,对两者之间的函数关系做进行一步的分析。首先对C1-IH在其取值范围内进行拉丁超立方抽样,抽取5个样本,然后仿真计算出每个样本下的表面温度值,结果见表4。

表4 5个样本点Table 4 The five sample points
在Matlab中,以横轴为器件内部生成热,纵轴为器件表面温度值,将这5个样本点描绘在二维平面内,发现两者关系基本上在一条直线上,如图2所示。因此可以近似做出这样一个假设:在热仿真分析中,各器件表面温度值只与自身内部生成热有关,并且两者之间是线性关系。由于内部生成热是功率与体积的比值,体积为固定值,因此也可说元器件表面温度与器件功率呈线性关系。

图2 5个样本点在平面内分布Fig.2 The distribution of the five samples
2 PCBA热模型修正方法
基于以上结论,元器件表面温度值可表示为y=kgx+b,其中x为器件自身功率,k和b为两个待定系数。为实现高效的热模型修正,可以根据热测量值和这个关系式对要修正的功率值进行预测,从而实现以较少的有限元仿真计算获得较好的修正效果。要获得关系式中的两个待定系数,只需获得2组x,y值便可通过求解一元二次方程组解出k,b值。因此,PCBA的热模型修正方法可按以下步骤进行[12—14]:
1)对产品进行热测量试验,获得各主要器件表面上的热测量温度值T=[T1,T2,…,Tm],m表示元器件个数。
2)在热仿真软件(如Flotherm)中给出各器件的初始功率P1=[P11,P12,…,P1m]及设置其他各项参数,进行初始仿真计算后提取初始仿真各器件表面温度值T1=[T11,T12,…,T1m]。
3)对各器件功率值按照各自初始值的上下5%或10%进行摄动获得摄动后功率值P2=[P21,P22,…,P2m],并按照该功率值进行仿真计算获得第二次仿真各器件表面温度值T2=[T21,T22,…,T2m]。
4)计算各器件的待定系数k,b值:

5)将热测量值作为目标值,求出各器件预测所需修正功率值:

6)将修正后功率值带入有限元模型中,仿真计算得出修正后模型。
3 案例分析
下面以某机载电子产品中的某块PCBA为案列,采用上述方法对其进行热模型修正。
首先进行热测量试验获取主要器件上的热测量温度值,然后在Flotherm软件中进行初始仿真获得主要部件对应的仿真值,初始仿真结果如图3所示。经过对比发现,有3个器件上的温度仿真值与热测量值偏差较大需要进行修正。这3个器件的初始功率、热测量温度值、热仿真温度值以及热测量值与仿真值的相对误差见表5。

图3 初始仿真结果Fig.3 The initial simulation results

表5 初始功率及仿真值与热测量值结果对比Table 5 The comparison of the simulated values and the measured values
亦即各器件热测量值:T=[52.5,52,50.5];各器件初始功率:P1=[0.6,0.3,0.38];各器件初始仿真温度值:T1=[47.6,49.6,48.9]。
1)对各器件功率值按照各自初始值的上下10%进行摄动获得摄动后功率值P2=[0.66,0.33, 0.418],并按照该功率值进行仿真计算获得第二次仿真的各器件温度值T2=[48.3,50.6,49.9]。
2)计算各器件的待定系数k,b值:k=[11.67, 33.33,26.32];b=[40.6,39.6,38.9]。
3)将热测量值作为目标值,求出各器件预测所需修正功率值:P'=[1.02,0.372,0.441]。
4)将修正后功率值带入有限元模型中,仿真计算得出修正后模型,模型修正后器件仿真温度值:T'=[50.9,52.4,51.2]。
模型修正后各器件表面温度热测量值与仿真值结果对比见表6;模型修正前后各器件功率值对比见表7;模型修正前后各器件表面温度的热仿真值与热测量值之间相对误差对比见表8。从表8中可以看出,采用这种方法对该热模型修正之后,各器件表面上的温度热仿真与热测量值之间的相对误差均明显减小。其中最明显的是器件U21,表面温度的相对误差由-9.33%减小到了-3.05%,而且整个模型修正过程只进行了2次有限元计算,从而验证了采用该方法进行热模型修正的精确性和高效性,可以推广到工程应用中。

表6 模型修正后热测量值与仿真值结果对比Table 6 The comparison of the simulated values and the measured values after model updating

表7 模型修正前后功率值对比Table 7 The comparison of power before and after model updating

表8 模型修正前后热仿真值与热测量值相对误差对比Table 8 The comparison of relative error of the simulated values and the measured values before and after model updating
4 结论
1)基于拉丁超立方抽样试验设计和Speraman等级相关系数计算公式的相关性分析方法可以从全局的角度考量输入参数对输出的影响程度,从而准确地为热模型修正筛选出待修正参数。
2)在得出器件表面温度与其自身功率呈线性关系的基础上,文中提出的热模型修正方法可以准确地对PCBA热模型进行修正,并且整个修正过程只需调用2次有限元软件,因而具有较强的工程应用价值。
[1] 刘娜.随机近似热模型修正方法及相变热控关键问题研究[D].合肥:中国科学技术大学,2012. LIU Na.Research on Stochastic Approximation Thermal Model Updating Method and the Key Problem of Phase Change Thermal Control[D].Hefei:University of Science &Technology of China,2012.
[2] 费庆国,韩晓林,苏鹤玲.响应面有限元模型修正的实现与应用[J].振动、测试与诊断,2010,30(2):132—134. FEI Qing-guo,HAN Xiao-lin,SU He-ling.The Implementation and Application of Finite Element Model Updating Based on Response Surface[J].Journal of Vibration, Measurement&Diagnosis,2010,30(2):132—134.
[3] HEINONEN O,PAJUNEN S.Optimal Design of Stiffened Plate Using Metamodeling Techniques[J].Journal of Structural Mechanics,2011,44(3):218—230.
[4] FRISWELL M I,MOTTERSHEAD J E,AHMADIAN H. Combining Subset Selection and Parameter Constrants in Model Updating[J].Journal of Vibration and Acoustics, 1998,120(4):854—859.
[5] FRISWELL M I,GARVEY S D,PENNY J E T.The Convergence of the Iterated IRS Method[J].Journal of Sound and Vibration,1998,211(1):123—132.
[6] MONTGOMERY D C.试验设计与分析[M].北京:中国统计出版社,1998:563—575. MONTGOMERY D C.Design and Analysis of Experiments[M].Beijing:China Siatistics Press,1998:563—575.
[7] DOUGLES C.Montgomery Design and Analysis of Experiments[M].2003.(余不详)
[8] 庄楚强.应用数理统计基础[M].第4版.广州:华南理工大学出版社,1992. ZHUANG Chu-qiang.Application of Mathematical Statistics[M].4th Ed.Guangzhou:South China University of Technology Press,1992.
[9] 郭勤涛,张令弥,费庆国.用于确定性计算仿真的响应面法及其试验设计研究[J].航空学报,2006,27(1): 55—61. GUO Qin-tao,ZHANG Ling-mi,FEI Qing-guo.Response Surface Method and Its Experimental Design for Deterministic Computer Simulation[J].Journal of Aeronautics, 2006,27(1):55—61.
[10]KWON J,HWANG S,LEE C,et a1.Application of Response Surface Methodology in Microspeaker Design Used in Mobile Phones[J].Institute of Electrical and Electronics Engineers Transactions on Magnetics,2009,45(10): 4550—4553.
[11]费庆国,张令弥,李爱群,等.基于统计分析技术的有限元模型修正研究[J].振动与冲击,2005,24(3): 23—26. FEI Qing-guo,ZHANG Ling-mi,LI Ai-qun,et a1.The Finite Element Model Updating Based on Statistical Analysis Techniques[J].Journal of Vibration and Shock,2005,24 (3):23—26.
[12]王红芳,赵玫.基于动态特性的印制板结构改进[J].振动与冲击,2000,19(1):49—51. WANG Hong-fang,ZHAO Mei.The Structure Improvements Based on the Dynamic Characteristics of the Printed Circuit Board[J].Journal of Vibration and Shock,2000, 19(1):49—51.
[13]杨宇军,叶松林,游少雄,等.插板式PCB的内置式减振设计方法及其PSD动力学仿真[J].振动与冲击, 2007,26(2):39—42. YANG Yu-jun,YE Song-lin,YOU Shao-xiong,et a1.The Vibration Damping Design Method of PCB and Its PSD Dynamics Simulation[J].Journal of Vibration and Shock, 2007,26(2):39—42.
[14]KWON J,HWANG S,LEE C,et a1.Application of Response Surface Methodology in Microspeaker Design Used in Mobile Phones[J].Institute of Electrical and Electronics Engineers Transactions on Magnetics,2009,45(10): 4550—4553.
Study on the Method of Thermodynamics Model Updating of Printed Circuit Board Assembly
WANG Kai-shan,LI Chuan-ri,GUO Heng-hui,PANG Yue-chan,LI Peng
(Reliability and System Engineering Institute,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
Objective To update the thermodynamics model of the printed circuit board assembly accurately and efficiently.Methods The input parameters with great effects on the surface temperature of a component in the thermal simulation test were found out through the correlation analysis method which was based on the Latin hypercube sampling experiment design and the computational formula of Speraman rank correlation coefficient.And then the function relationship between the input and output was obtained after further analysis.On this basis,the general process of the thermodynamics model updating of the printed circuit board assembly was provided.Finally,the thermodynamics model of a PCBA from an aircraft electronic product was updated with this method.Results The result of the updated model showed good accuracy and only two calls to finite element software.Conclusion This method of thermodynamics model updating had good accuracy and efficiency,and could be used in engineering practice.
Latin hypercube sampling;Speraman rank correlation coefficient;parameter screening;thermodynamics model updating
LI Chuan-ri(1964—),Male,Professor&Researcher,Research focus:product environmental engineering and reliability test technology.
10.7643/issn.1672-9242.2014.05.023
TN41
:A
1672-9242(2014)05-0119-06
2014-07-14;
2014-08-19
Received:2014-07-14;Revised:2014-08-19
王开山(1990—),男,江苏徐州人,在读硕士,主要研究方向为产品环境工程。
Biography:WANG Kai-shan(1990—),Male,from Xuzhou,Jiangsu,Master student,Research focus:Product Environmental Engineering.
李传日(1964—),男,教授,研究员,主要研究方向为产品环境工程,可靠性试验技术

