地质统计学在三道庄钼矿储量计算中的应用
李 亮,徐娟娟,叶会寿
(1.昆明理工大学 国土资源工程学院,云南 昆明 650093)
(2.洛阳栾川钼业集团股份有限公司,河南 栾川 471542)
(3.中国地质科学院矿产资源研究所,北京 100073)
0 前言
地质统计学是法国著名统计学家G.Matheron于20 世纪60 年代在大量理论研究的基础上创立并发展的一门集数学与地质采矿为一体的边缘学科,目前已在国内外获得广泛应用。它是以区域化变量理论作为理论基础,以变异函数为主要工具,采用不同的克立格方法,对在空间上既有随机性又有结构性的变量(如品位值)进行研究的科学。经过40 多年的发展,目前已经形成了一套较为完整的理论体系[1-2]。本文利用矿业工程软件,运用地质统计学原理和方法,对三道庄钼矿床进行研究。采用最优、线性无偏估计研究钼矿石品位的空间变异性,并计算给定边界品位下的矿石的储量,为矿山资源合理开发利用提供有意义的决策依据。
1 矿床地质概况
三道庄钼矿床位于河南省栾川县境内,矿床中心地理坐标为东经111°29'40″、北纬33°55'00″,钼资源量丰富,为特大型钼矿床[3]。该矿床位于华北地台南缘褶皱带卢氏—栾川多金属成矿带中的南泥湖钼矿田内,区内地层、构造、变质带及岩浆岩均呈北西西-北西向分布。三道庄钼矿主要矿体为大厚度的似层状矿体,呈扇形产于岩体外接触带三川组上段的矽卡岩、钙硅酸角岩及南泥湖中段的黑云母长英角岩中。在主矿体的上、下部位有少数零星小矿体分布。此外,在主矿体顶、底板有分枝复合及褶皱构造转折处有膨胀狭缩等现象[3-4]。矿体形态、产状受岩性、构造、岩浆岩控制较为明显。矿体的分布范围、产状与钙硅酸角岩、矽卡岩及岩浆岩缓倾斜部位的分布范围、产状相一致。矿体走向280°~310°,倾向南西,倾角较为平缓。主矿体沿走向在矿区范围内长度大于1 420 m,沿倾向长度大于1 120 m,厚度一般80~150 m,最大厚度可达364.56 m,厚度变化系数为44%~60%[3-4](图1)。
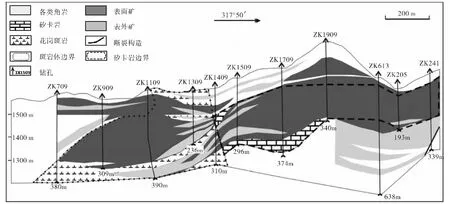
图1 三道庄钨钼矿区横9 线勘探剖面
2 数据选取及数据库的建立
根据研究需要,选取三道庄钼矿体主要成矿组分钼为研究对象,共收集了矿体上146 个地表勘探钻孔共21 107 件样品,钼化验分析数据208 97 件。这些样品大多来自河南省地质矿产局第一地质调查大队在20 世纪70 年代矿床详细勘探过程中所采集的样品,部分为后期矿山基建勘探所采集的样品。将这些数据以特定格式录入计算机中,利用Surpac专业软件将收集到的每一个样品化验数据连同其对应的三维坐标及其他属性(样号、化验数据、岩性、勘探工程编号、勘探时间等)存入数据库中。
3 数据的统计分析
在地质统计学中,计算实验半变异函数之前,首先按照有效数据须确定在建立长度的支撑上的要求,即对参与计算的所有样品数据进行重新组合,使同类参数的地质样品段的长度达到一致[2,5]。因此,必须对样长不等的钻孔原始数据按一定的长度进行重新组合计算,并对原始数据进行等长组合处理。在组合过程中,笔者根据三道庄矿床钻孔的特点和矿体研究的技术要求,采用2 m 的长度进行样品组合,并对组合后的样品进行统计分析,钼品位分布特征结果参数见表1。

表1 三道庄钼矿床组合样品统计分析结果
由于有用元素在地质环境中自然富集,造成部分样品元素品位相对较高,不能真实地反映矿体的实际分布特征,因此需要进行特高品位的处理[5]。根据矿山勘探报告对特异值的识别及处理原则,笔者选取97.5%的置信区间处的样品值0.296%,将其定为特高品位下限,对特高品位进行处理,然后对钼品位分布进行统计分析。研究发现,钼品位分布呈现非正偏斜,表现为右偏,不服从正态分布(图1-a),将组合样品位进行对数转换后,采用正态分布的峰度偏度检验法,发现钼组合样品位基本服从三参数的对数正态分布(图1-b)。因此可以利用转化后的数据进行变异函数计算,并且可以选用克立格方法对矿体进行品位估值和储量计算。

图2 钼品位及钼品位经对数转换后的分布直方图
4 变异函数模型的建立
4.1 实验变异函数的计算
在经典统计学中,通常采用均值、方差、标准偏差、变化系数等一类参数来概括反映地质体的全貌(如各元素总的变化情况),却无法反映局部范围和特定方向上地质特征的变化,这是因为经典统计学只考虑数值大小,不考虑数据的空间位置关系。而在地质统计学中,研究矿床中金属品位分布特征的一个重要的方面就是掌握品位沿某一个或某几个方向或距离的变化规律,通常就采用变异函数来分析,它兼顾了品位数值大小和品位变化的空间位置关系,使得统计的品位分布特征更趋于合理[6-7]。
所谓变异函数就是假设在一个空间中的某个域V,V 内区域变化量按一定方向间隔的两点x,x+h的变化程度,变异函数反映了区域变化量的结构特征和空间连续性。但是在实践中,往往样品的数目总是有限的,把用有限的实际采集的样品值构制成的变异函数称为实验变异函数,实验变异函数就是根据实际所取数据构造变异函数γ(h)的估计值γ*(h)

式中,γ*(h)为实验变异函数;h 为滞后距,即在一定方向上,距离为| h |的矢量;N(h)表示滞后距为h 时参加实验变异函数计算的样品对数;Z(xi),Z(xi+h)为区域化变量在空间点上的品位的测定值[8-9]。
对组合样品位数据进行变异函数曲线分析,分析其空间变异特征,是研究矿体变化性以及计算矿体储量必不可少的步骤[6]。由于三道庄钼品位数据服从三参数的对数正态分布,因此在本次计算三道庄钼品位实验变异函数时,首先需将钼元素组合样的品位数据进行对数转换,选取经过对数转换处理后的数据作为区域化变量,根据钼矿体成矿地质特征,选择分别在矿体走向、倾向、厚度3 个方向,即对应为变异函时绘制了实验变异函数曲线图。从图3、图4、图5 中曲线A 可以看出3 个方向的曲线波动性都较小,说明三道庄钼矿体钼品位变化较小、分布较均匀。
4.2 理论变异函数曲线拟合
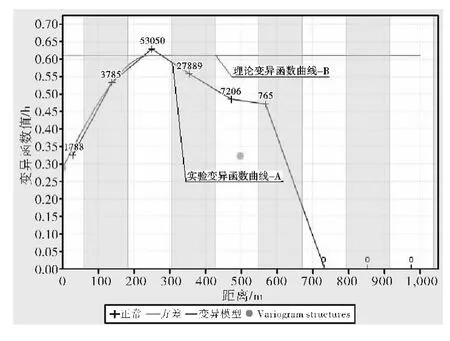
图3 钼品位厚度方向实验变异函数曲线及其拟合曲线

图4 钼品位倾向方向实验变异函数曲线及其拟合曲线
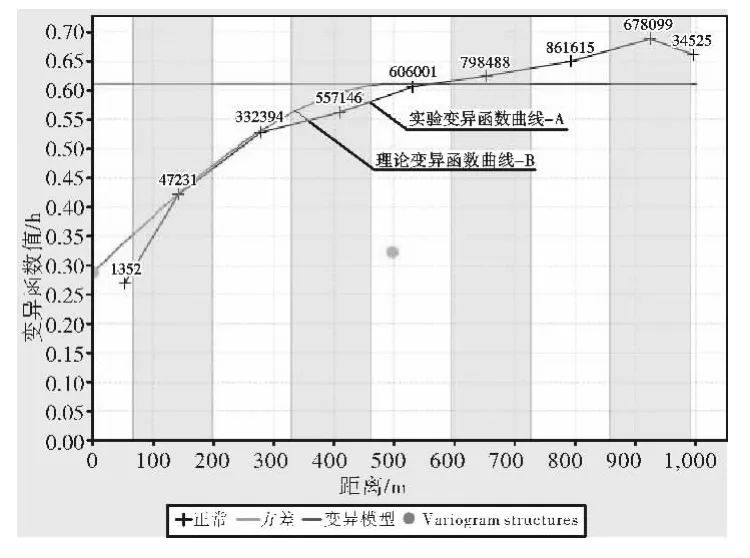
图5 钼品位走向方向实验变异函数曲线及其拟合曲线
从三道庄钼矿体钼品位分布得出的实验变异函数曲线的特征来看(如图3、图4、图5 中曲线A),虽然数据点的分布规律性相对较差,但仍可看出变异函数γ(h)随距离h 首先增加,然后趋于稳定,符合球状模型的特点,因而采用实验变异函数球状模型用加权多项式回归法分别对走向、倾向、厚度3 个方向进行拟合。球状模型公式为:

式中C0为块金常数;C0+C 为基台值;a 为变程;h为滞后距。
从公式(2)中可以看出,γ(h)随h 的增加而增加,当h 达到变程时,γ(h)达到基台值C0+C;之后γ(h),便保持常值C0+C。这种特征的物理意义是:当样品之间的距离小于变程时,样品是相互关联的,关联程度随间距的增加而减小,或者说,变异程度随间距的增加而增大;当间距达到一定值时,样品之间的关联性消失,变为完全随机,这时γ(h)即为样品的方差。因此,变程实际上代表样品的影响范围[9-11]。
通过对三道庄钼矿体钼品位3 个方向实验变异函数的研究,发现它们都可以用1 个带有块金常数的球状模型进行拟合,经过反复实验,确定三道庄钼矿体钼品位的理论变异函数曲线,如图3、图4、图5中B 所示:
从图3、图4、图5 图中曲线B 可以看出,三道庄钼矿体钼品位变异函数在3 个方向上的基台值(C0+C)都基本相同,而变程(a)不同,表现出各向异性的特征。同时,钼的品位在走向方向变程最大,厚度方向最小,说明了钼矿化的连续性在走向方向上较其它两个方向强,而厚度方向的连续性最弱,这与矿床地质成因是相一致的。求得球状模型的参数如下:

其在各个方向上的变异函数分别表示为:
矿体厚度方向:
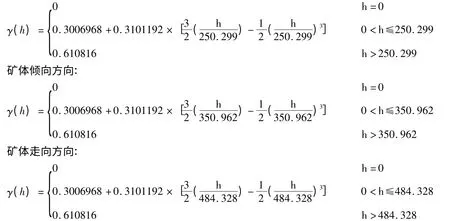
从以上3 个变异函数公式表明三道庄钼矿床钼品位变异函数具有方向上的异向性,即在不同方向上表现为基台值相同,变程不同的几何异向性,各向异性比为:

在本次研究中,笔者用带状各向异性对模型进行套合(带状各向异性模型几乎可用于任意试验各向异性模型),变异函数的套合结构为:
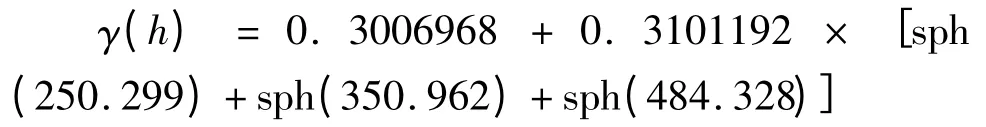
式中sph(250.299)、sph(350.962)和sph(484.328)分别表示变程为250.299 m、350.962 m 和484.328 m 的球状模型。其相应的转换矩阵为:

通过以上对矿体各方向变异函数的计算及曲线的模拟,可以确定三道庄钼矿体钼品位的变异函数具有几何异向性,空间各方向的变程(距离)构成了变程各向异性。
4.3 变异函数交叉验证
为了对结构模型进行检验,采用了交叉验证方法,以判断变异函数拟合参数的选取是否正确。交差验证是用来检验变异函数曲线拟合的可靠性,并辅助确定变异函数参数。其基本方法是:利用所得结构模型和已知样品去估已知值,然后把这些真值和估计值进行比较,对两者的残差(差值)进行统计分析,以判断变异函数结构的正确性[8,9,12]。交叉验证结果见表2、图6、图7。

表2 残差统计参数一览表
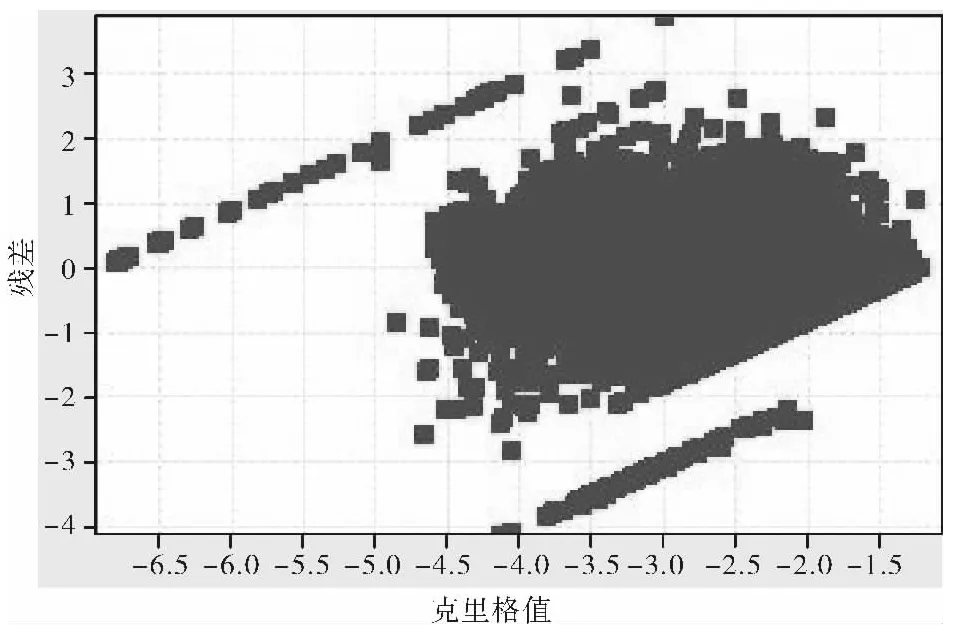
图6 残差VS 品位统计图

图7 钼品位交叉检验残差分布直方图
通过验证计算,经对数转换后的钼组合样品位实际值与估计值之间的误差均值趋近于零,即误差的均值趋近于零(图6);经对数转换后的钼组合样品位实际值与估计值之间的单个偏差趋近于零,且趋近于平均克立格方差,即误差的方差趋近于零且方差比趋近于1;残差分布属于正态分布,且95%置信限位于正负两倍的克立格方差范围内(图7)。以上结果表明模型确定合理,变异函数参数对经转换后的钼品位进行估计是无偏的,满足足区域化变量内蕴假设,从而验证了变异函数模型是正确的,可以用于下一步的矿床钼品位估值和资源储量计算。
4.4 克立格法品位估值
完成变异函数模型结构分析,充分了解了三道庄钼矿体的空间变异性,下一步工作是设计克立格估值方案。克立格法是根据代估样本点(或块段)有限邻域内若干已测定的样本点数据,考虑了样本点的形状、大小和空间相互位置关系,与待估样本点的相互空间位置关系,以及变异函数提供的结构信息,对待估样本点值进行的一种线性无偏最优估计[14]。
地质统计学主要是在结构分析的基础上采用各种克立格法来估计和解决实际问题。根据研究的目的和条件的不同,主要划分为普通克立格法、泛克立格法、对数正态克立格法、指示克立格法等,在不同的条件下应选取适当的方法进行估值,其中最基本、应用最为广泛的是普通克立格法[10-14]。普通克立格法适用于满足二阶平稳(或内蕴)假设的矿床。综合分析针对三道庄矿床钼元素品位满足内蕴假设条件,选择采用普通克立格法进行矿床品位估值。其克立格主要参数设置如下:椭球体定向方位为300°、倾伏角为0°、倾角为18°;各项异性比率为1∶1.38∶1.935;最大距离分别选取110 m,220 m,440 m;最少样品和最多样品总数分别设置为3 个和16 个。结合已经得到的理论变异函数参数值(块金值、基台值、变程等),从而完成对矿床钼品位的估值。
5 储量计算
根据组合样最低品位值限制,按边界品位0.03%,矿石体积质量取3.2 t/m3进行储量统计计算。将储量计算结果与采用传统平行断面法计算结果进行验证对比,结果如图表3 所示。
从对比结果可以看出,采用普通克立格法计算矿体资源量与采用传统平行断面法计算的矿体资源量基本吻合,其误差基本在5%左右,说明应用普通克立格法对矿体资源量的估算是可靠的。所对应的钼品位—吨位曲线见图8。
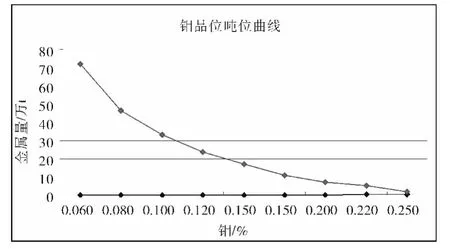
图8 三道庄钼矿床钼品位—吨位曲线
从图8 可以看出,随边界品位的逐渐增高,矿体的平均品位逐渐升高,钼资源金属量则不断减少,因此矿山可根据当前的金属价格和企业的生产成本,可以快捷准确地确定矿体的经济开采品位和吨位,为开采设计方案的优化提供可靠的依据。
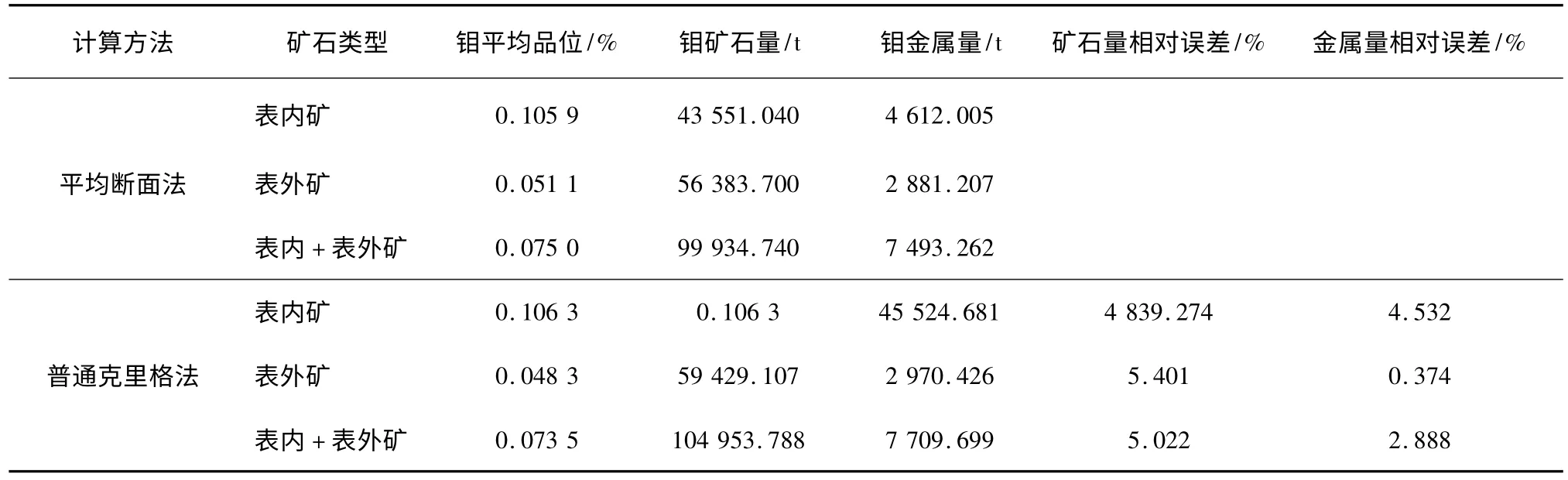
表3 平行断面法、克立格法储量计算结果对比表
随着地质统计学方法在矿产储量计算过程中的应用与发展,传统的储量计算方法(如地质块段法、平行断面法等)在计算较复杂的矿床时,受到了巨大挑战。通过本文的储量计算过程可以看出,基于Surpac 软件的地质统计学方法可以十分快捷地计算矿床储量,并提交储量报告。同时,可以根据不同需求及时绘制出新的指标下矿体的形态,并动态计算任意边界的矿产储量,大大节约了人力、物力和时间,提高了效率和精度。但是如果按照传统的方法,在改算矿体的储量时,必须重新圈定矿体和确定计算边界,这时工作量是非常大的,效率很低。因此应用地质统计学方法进行矿床储量计算具有十分明显的优势。
6 结论
(1)笔者综合运用地质统计学理论,建立了三道庄钼矿床数学模型,通过对钼品位变异函数分析,发现厚度、倾向、走向3 个方向的曲线波动性均较小,且均有较大的变程,说明三道庄钼矿体钼品位空间分布具有较好的连续性,矿体内部品位分布较均匀。
(2)通过对比分析普通克立格法和传统平行断面法计算矿体的资源量,结果表明:所建立的三道庄钼矿床数学模型可靠,所选用的区域化变量和模型估值方法合理,所采用的变异函数模型及其参数计算正确,可用于辅助矿山进行资源评估、采矿设计以及计划编制等工作。
(3)地质统计学方法与传统的储量计算方法相比具有明显的优点。它能最大限度地利用现有的勘探工程所提供的资料,使计算的矿石品位和矿石储量更为精准和快捷。
[1]侯景儒.实用地质统计学[M].北京:地质出版社,1998:2-6.
[2]侯景儒,黄竞先.地质统计学及其在矿产储量计算中的应用[M].北京:地质出版社,1982:31-46.
[3]瓮纪昌,张云政,黄超勇,等.栾川三道庄特大型钼钨矿床地质特征及矿床成因[J].地质与勘探,2010,46(1):41-48.
[4]汪江河.河南三道庄钨钼矿区深部下层矿的找矿意义[J].地质调查与研究,2009,32(4):292-296.
[5]郑文宝,黎枫佶,唐菊兴,等.基于Micromine 软件下地质统计学在甲玛矽卡岩型铜多金属矿储量计算中的应用[J].地质与勘探,2011,47(4):726-736.
[6]孙洪泉.地质统计学及其应用[M].北京:中国矿业大学出版社,1990:59.
[7]Surpac software 国际软件公司.Surpac Vision 地质统计学培训资料[R].北京:2012.
[8]罗周全,刘晓明,吴亚斌,等.地质统计学在多金属矿床储量计算中的应用研究[J].地质与勘探,2007,43(3):83-87.
[9]余海军,李文昌,尹光候,等.普朗铜矿床铜品位分布地质统计学研究[J].地质与勘探,2009,45(4):437-443.
[10]陈爱兵,秦德先,张学书,等.基于MICROMINE 矿床三维立体模型的应用[J].地质与勘探,2004,40(5):77-80.
[11]贾明涛,潘长良,王李管.克服地质统计学矿床建模中主观因素影响技术研究[J].地质与勘探,2003,39(4):73-77.
[12]余海军,李文昌,曾普胜,等.地质统计学在羊拉铜矿储量计算中的应用[J].地球学报,2009,30(5):684-690.
[13]徐 静,胡乃联.Surpac 软件在某金铜矿山的应用研究[J].黄金科学技术,2007,15(1):54-58.
[14]冯超东,杨 鹏,胡乃联.克立格法在SURPAC 软件中的实现及应用[J].金属矿山,2007,370(4):55-58.

