稀疏主成分简介*

山西医科大学卫生统计教研室（030001） 田双双 张海霞 赵俊琴 乔 楠 王 彤

稀疏主成分简介*

山西医科大学卫生统计教研室（030001） 田双双 张海霞 赵俊琴 乔 楠 王 彤△

主成分分析（principal component analysis，PCA）是一种很受欢迎的统计降维方法，可将多个指标简化为少数几个不相关的综合指标。我们可以利用PCA从事物之间错综复杂的关系中找出一些主要的成分，从而有效地揭示变量之间的内在关系［1］。生物信息学获取的数据往往需要降维处理，这就为PCA的应用提供了机会，例如Hastie［2］等2000年提出的“geneshaving”就是利用PCA对基因数据进行聚类。然而基因数据往往具有“超高维”的性质，也就是说基因个数呈样本量的指数级增长，由于传统的主成分都是原始变量的线性组合，线性组合中的回归系数（因子载荷）往往是非零的，这些非零的回归系数值使得PCA的结果很难解释。事实上这也是PCA应用于高维生物信息数据分析结果解释中的一个弊端。

Tibshirani（1996）［3］提出的LASSO（least absolute shrinkage and selection operator）可以得到稀疏解，也就是可以使回归系数（因子载荷）的值为零。Jolliffe［4］2003年受LASSO的启发，直接将LASSO惩罚引入主成分，并在2006年提出了相应的算法。Zou［5］等（2006）将主成分的求解问题转化为LASSO回归问题，这样稀疏主成分的求解问题就有效地转化为线性模型的变量选择问题。在此基础上引入弹性网（elastic net）或其他惩罚结构，于是得到了稀疏主成分（sparse principal component analysis，SPCA）。稀疏主成分在降维的同时可以令某些变量对应的因子载荷系数等于零，可以更合理地解释降维结果，有效揭示数据的内在结构［6］。

原理和方法

1.LASSO及其相关方法

LASSO是一种很受欢迎的降维和参数估计方法，它是对回归系数加以L1惩罚，通过惩罚回归系数的数量来进行降维，可以解决共线性问题［7］。表达式如下：

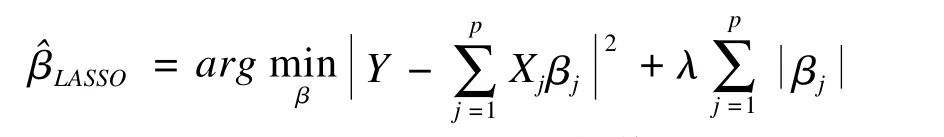
因此βlasso可以在λ是一个非负值时，通过最小化LASSO准则得到。LASSO不断地压缩回归系数趋向于0，通过偏方差权衡增加了预测精度。因此，LASSO同时提高了模型的精确性和稀疏性。LASSO刚提出时缺乏有效的算法，Efron［8］（2004）提出的最小角回归（least angle regression，LARS）很好地解决了LASSO的计算问题，使得LASSO方法广为流行。但是，LASSO也存在一些问题，最显著的缺点是选择变量会受限于样本量。

弹性网（elastic net）是L1惩罚和L2惩罚的结合，克服了LASSO的一些不足，但仍具有LASSO理想的性质。对于任意非负的λ1和λ2，弹性网估计值βen可以由下式给出

可以看出，LASSO是当λ2＝0时弹性网的一种特殊情况。弹性网惩罚是ridge惩罚和LASSO惩罚的凸组合，给出一个特定的λ2，LARS-EN［9］（2003）算法可以算出所有的λ1的弹性网问题，其计算的复杂度和最小二乘回归相当。当P＞n时，选择λ2＞0，这样弹性网就可以把所有可能的自变量选入拟合模型，从而克服了LASSO的局限性。弹性网的另一个优势就是它的组效应，也就是说，一旦一组高度相关的自变量中的一个自变量被选入模型，那这一组自变量都会被选入模型。而LASSO只能选择一组相关自变量中的一个，而且不确定哪个自变量会被选入最终的模型。

SCAD（smoothly clipped absolute deviation）不仅具有LASSO和弹性网的稀疏性和连续性的优良性质，而且可以有效减小模型参数估计的偏性，并具有oracle性质［10］（稀疏性和渐近正态性）。SCAD的估计值表示为

上式有两个待估参数λ和aλ，这是因为自变量很多时，单个压缩参数λ不足以同时筛选变量并得到一致的估计。在SCAD中，当效应大于aλ时，惩罚项退化为一个常数，从而使得效应的估计没有偏倚。但SCAD惩罚是非凸的，这给处理带来了很大的困难，Zou和Li（2008）［11］提出局部线性近似（local linear approximation，LLA），然后采用LARS算法求解，可应用于凹惩罚函数的优化。

2.基于LASSO的简化主成分

Jolliffe［4］（2003）提出SCoTLASS（simplified component technique LASSO）的想法是为了使主成分得到稀疏解，将L1惩罚结构直接应用于主成分的求解，SCoTLASS可表述为如下优化问题：

3.稀疏主成分和惩罚回归的关系

Zou等［5］（2006）给出的SPCA更充分地运用了LASSO和弹性网。PCA中的每一个主成分都是p个自变量的线性组合，因此因子载荷可以通过对每个主成分做回归分析得到。下面我们系统地介绍一下稀疏主成分和惩罚回归的关系。

首先，设Yi＝UiDi为第i个主成分，λ＞0，则是由岭回归估计值得到，并且设由此可见将回归分析与主成分分析联系起来具有一定的可行性，这样主成分的求解就可以转化为线性模型的求解问题。很明显，当n＞p且X是列满秩矩阵时，该定理中可以取λ＝0。但当p＞n且λ＝0时，普通最小二乘问题的解不唯一，这与n＞p且X不是列满秩的情形类似。然而PCA无论在什么情况下都能给出唯一解，是因为岭罚项的恒大于零消除了这种矛盾。但是此方法的缺点是依赖PCA的结果。接下来我们更进一步推广以上结论。

Xi是X的第i行向量，对于任意这样，我们直接根据回归知识就得到了第一主成分，可以不依赖PCA的结果。继续推广，假定我们只考虑前k个主成分令α和β分别为p×k的矩阵，Xi表示X的第i行向量，对任意的其中αTα＝Ik，则这样将主成分问题就有效地转化为一个回归问题，为了得到稀疏主成分，我们将LASSO惩罚加入到上式中，得到如下的最优化问题：

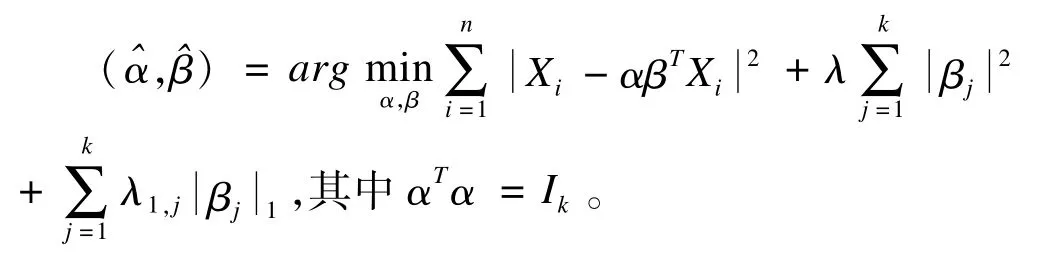
这一优化问题被称为SPCA准则，我们用一种交替最小化算法来最小化SPCA准则

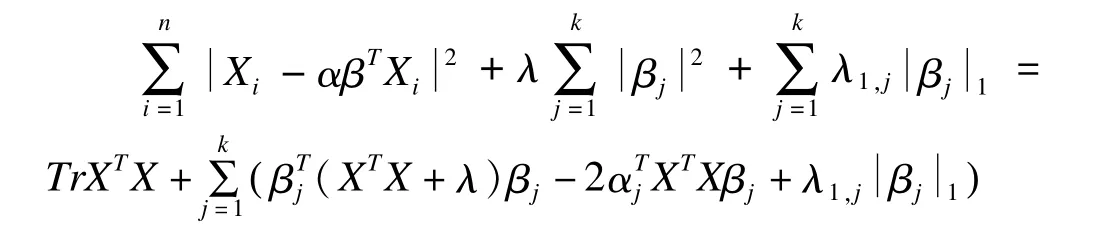
因此，给定α上式等价于解决k个独立的弹性网问题得到，j＝1，2，…，k

另一方面我们也可以得到

因此，给定β，我们需要最大化TrαT（XTX）β，其中αTα＝Ik。下面，我们来解决这一优化问题：

令α和β为m×k的矩阵并且β的秩为k，考虑如下最大化问题假定β的SVD分解为β＝UDVT，则有

由前述可知，稀疏主成分的求解可转化为惩罚回归问题。而一般的LASSO惩罚回归问题又可以通过最小角回归算法来解决。因此，稀疏主成分的计算也可以利用最小角回归算法方便给出。

由此，得到一般的稀疏主成分算法：

（1）计算一般主成分的前k个主成分对应的向量

（2）在给定α＝（α1，…，αk）的情况下解决如下的弹性网回归问题：

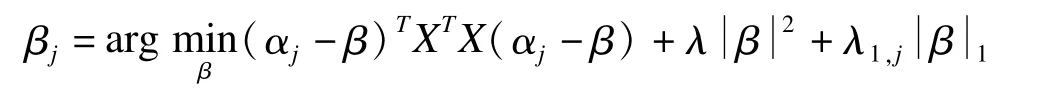
（3）对于给定的β＝（β1，…，βk），计算XTXβ＝UDVT的SVD，并且令α＝UVT

（4）重复步骤2、3至β收敛

模拟研究

为了说明稀疏主成分在降维和变量选择上的优势，我们用R软件展示一个模拟的例子。首先，我们定义三个潜在的因子：

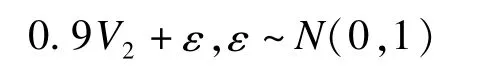
V1，V2和ε是独立的。

假设有15个变量（X1，X2，…，X15），其中5个变量（X1，X2，X3，X4，X5）由V1生成，5个变量（X6，X7，X8，X9，X10）由V2生成，5个变量（X11，X12，X13，X14，X15）由V3生成。以下是具体的生成方式：

使用传统PCA和SPCA得到结果如表1所示。

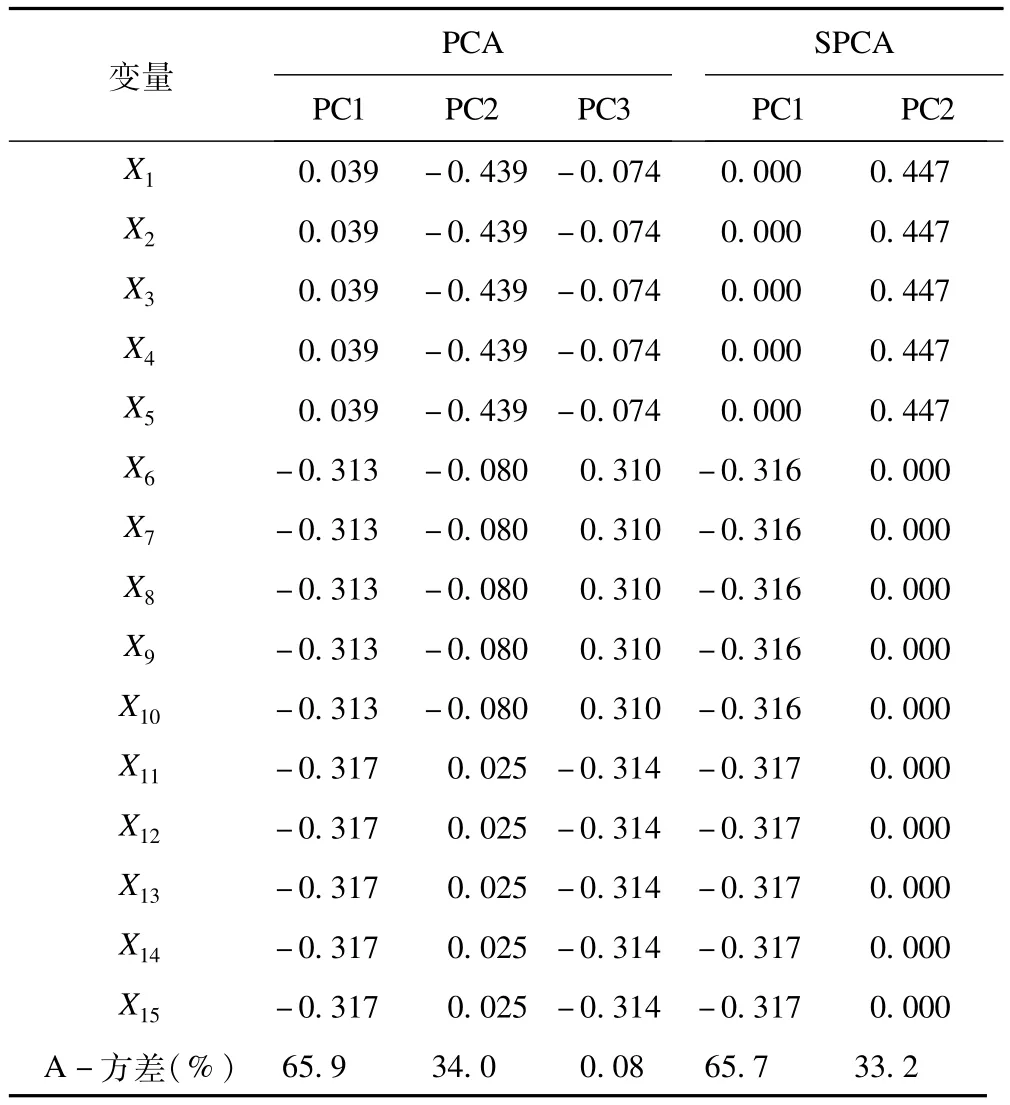
表1 PCA和SPCA的结果

从结果可以看出，PCA前两个主成分的方差贡献率达99.9%，SPCA的前两个主成分的方差贡献率达98.9%。说明与PCA相比，SPCA在提取主成分的时候存在一定程度的信息缺失，但是可以准确反映数据的内在结构，提取了前两个主成分，并且产生了稀疏解。

在这个模拟中，SPCA采用弹性网作为惩罚函数，得到的第一主成分（PC1）提取出了V2和V3两个潜在的因子，验证了我们前面所说的弹性网的组效应，因为V3生成时和V2高度相关。

讨 论

本文系统地介绍了一种高维数据降维的方法——稀疏主成分分析，并采用模拟对该方法进行说明。结果表明：SPCA不仅达到了有效降维的目的，而且简化了主成分的解释，使提取的主成分往往能对应于某些变量的实际含义，更具应用价值。该方法与LASSO紧密联系在一起，所有对LASSO的改进都可以直接应用到SPCA。Leng＆Wang［12］（2009）在“Adaptivelasso”的启发下研究了简单自适应稀疏主成分（SASPCA）和一般自适应稀疏主成分（GAS-PCA），Lee［13］（2010）提出超稀疏主成分（super-sparse principal component analysis，SSPCA）以解决SPCA在基因微阵列数据中得到的解不够稀疏的情况。在应用方面，除了金融，SPCA在基因等高通量数据的处理上较PCA更有优势，因为它可以降低非零回归系数的比例。Lee［14］（2012）将SPCA应用于全基因组关联性研究（GWAS），从肠炎的基因组SNP信息中识别出血统信息（AIMs）。考虑到主成分方法本身已得到广泛应用，结合高维数据降维结果解释稀疏解的优势，稀疏主成分方法有望随着LASSO等相关技术的发展而得到欢迎。

1.张新波.稀疏主成分及其应用.中南大学，2008.

2.Hastie T，Tibshrani R，M icheal BE，et al.′Gene shaving′as a method for identifying distinct sets of genes w ith sim ilar expression patterns. Genome Biology，2000，1（2）：0003.1-0003.21.

3.Tibshrani R.Regression Shrinkage and Selection via the LASSO.Journal of the Royal Statistical Society，1996，58（1）：267-288.

4.Jolliffe LT，Trendafilov NT，Uddin M.A Modified Principal Component Technique Based on the LASSO.Journal of Computational and Graphical Statistics，2003，12（3）：531-547.

5.Zou H，Hastie T，Tibshrani R.Sparse Principal Component Analysis. Journal of Computational and Graphical Statistics，2006，15（1）：265-286.

6.刘超，吴丹丹，杨考.一种新的高维数据降维方法.统计与咨询，2012，04：16-17.

7.闫丽娜，覃婷，王彤.LASSO方法在Cox回归模型中的应用.中国卫生统计，2012，29（1）：58-60，64.

8.Efron B，Tibshirani R，Johnstone L，et al.Least angle regression.The Annals of Statistics，2004，32（2）：407-451.

9.Zou H，Hastie T.Regression Shrinkage and Selection via the Elastic Net，w ith Applications to M icroarrays.Technical report，Department of Statistics，Stanford University.Available at http：//www-stat.stanford. edu/～hastie/pub.htm，2003.

10.Fan JQ，LiRZ.Variable Selection via Nonconcave Penalized Likelihood and its Oracle Properties.journal of the American Statistical Association，2001，96（456）：1348-1360.

11.Zou H，Li R.One-step Sparse Estimates in Nonconcave Penalized Likelihood Models.Ann Stat，2008，36（4）：1509-1533.

12.Leng CL，Wang HS.On General Adaptive Sparse Principal Component Analysis.Journal of Computational and Graphical Statistics，2009，18（1）：201-215.

13.Lee D，LeeW，Lee Y，et al.Super-sparse principal component analyses for high-throughput genomic data.BMC Bioinformatics，2010，11：296.

14.Lee S，Epstein MP，Duncan R，et al.Sparse principal component analysis for identifying ancestry-informativemarkers in genome-wide association studies.Genet Epidemiol，2012，36（4）：293-302.

（责任编辑：郭海强）

*：国家自然科学基金（81072385）；全国统计科研计划重点项目（2009LZ033）

△通信作者：王彤，E-mail：w tstat＠21cn.com