非独立数据时稳健Poisson和Log-binom ial随机效应模型研究*

周舒冬郜艳晖△李丽霞张 敏杨 翌陈 跃

非独立数据时稳健Poisson和Log-binom ial随机效应模型研究*

周舒冬1郜艳晖1△李丽霞1张 敏1杨 翌1陈 跃2

目的比较基于稳健Poisson回归及Log-binom ial的随机效应模型对具有层次结构的非罕见结局事件资料的参数估计结果。方法通过计算机模拟生成具有类内相关的数据集，设置了32种参数情况，分别反映实际资料中的少数类别数和中等类别数，小强度的类内聚集和中等强度的类内聚集，基线患病率分别为0.15和0.3，关联强度PR值分别是1.5和2.0，暴露率分别为20%和50%的情况；比较各模型在模拟条件下的收敛率、参数估计结果以及参数的95%CI覆盖率。结果Log-binomial随机效应模型的收敛效果劣于稳健Poisson随机效应模型；两随机效应模型对各参数的估计结果均和真值较为接近；在类内聚集性较小时，两随机效应模型95%CI覆盖率均较好，但随类内聚集性增大，Log-binom ial的随机效应模型95%CI覆盖率变动较大，且类别数增加时覆盖率普遍较低。结论基于稳健Poisson的随机效应模型收敛率高，参数估计结果与真实值接近，对各固定效应参数估计的95%CI的覆盖率高且稳定，优于Log-binomial随机效应模型。

非独立 稳健Poisson回归 Log-binom ial模型 随机效应 患病率比

流行病学封闭性队列研究和横断面研究中，OR值被广泛应用于RR/PR的近似估计，但研究结局出现频率较高（如大于10%）时，会严重高估暴露对结局的影响，这一问题早已引起统计学者注意，因此直接估计RR/PR的模型被提出，如Log-binomial模型和稳健Poisson回归模型，其参数解释更为合理［1］。但基于稳健Poisson回归和Log-binom ial模型的相关理论和应用研究尚显不足，因此本研究通过计算机模拟，探讨稳健Poisson和Log-binomial的随机效应模型参数估计的有效性及应用中的相关问题。

模型原理与方法

本研究以方差分量模型为基础，探讨基于稳健Poisson回归及Log-binomial的随机效应模型。

1.稳健Poisson随机效应模型

设yki和Xki＝（x1ki，x2ki，…，xpki）T分别为第k（k＝1，2，…，K）类内第i（i＝1，2，…，nk）个个体的二分类结局变量和P×1维解释变量向量，uk为第k类的随机效应，则构建随机效应模型：

式中，pki＝Pr（yki＝1｜Xki），连接函数采用log函数，βp为固定效应参数，反映固定效应xp对结局概率对数的影响，且RR（PR）＝exp（βp）；假定随机效应uk来自正态分布总体，即随机效应方差的大小反映结局变量在类内的聚集程度。

当误差分布指定为Poisson分布时，由于Poisson分布的方差无边界（方差等于均数），当应用到二项分布资料时，易出现过度离散问题，即高估参数的方差，导致较宽的置信区间。处理高估方差的一个经典方法是引入Huber的稳健“三明治”方差：

其中，

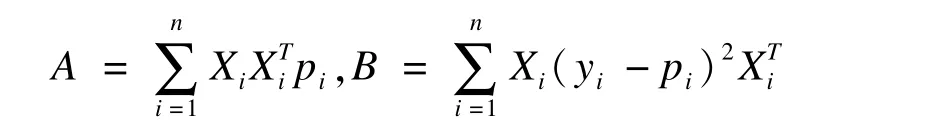
从而构建稳健Poisson随机效应模型。

2.Log-binomial随机效应模型

Log-binom ial随机效应模型同式（1），但误差分布指定为二项分布。应用于独立数据时，基本的Log-binom ial模型最大似然估计时需加一个限制条件，对所有个体，令

最大似然估计的解应该在此条件限制的参数空间中。Log-binomial模型在参数估计过程中，最大似然估计的解如果落在有限制的参数空间边界上，易出现不收敛的情形，模型中包含连续型协变量时尤甚。实际工作中经验性地设置截距β0＝-4可能效果较好［2］，Deddens建议也可先对原始数据集调整扩充后再拟合Log-binomial模型，即可得到参数的近似最大似然估计（maximum-likelihood estimation，简称MLE）值，称为COPY算法［3］，独立数据情况下，其收敛性和近似MLE的唯一性已有严格的理论证明［4］。

目前稳健Poisson和Log-binomial的随机效应模型都可在SAS中采用Proc Glimmix过程实现，连接函数选用log连接，误差分布分别指定为Poisson分布和二项分布，并用random语句指定截距项以拟合方差分量模型。

模拟研究

1.模拟方法及参数设置

模拟研究生成具有类内相关的数据集，按log-binomial随机效应模型产生。数据集中包含两个自变量X1和X2，假定X1为二分类自变量（1＝暴露；0＝非暴露），X2为连续型协变量；Y为二分类因变量（1＝结局发生；0＝结局未发生）。每个数据集共有N类，每类包括Nk个个体，因变量Y具有类内相关，类间独立的特性。

（1）类别数N和类内个体数Nk的设置

假定每个数据集的平均样本量为500，模拟类别数N为20和50两种情况。类别数N＝20时，类内个体数Nk由均匀分布U（0，50）随机产生，即Nk的均数为25；类别数N＝50时，类内个体数Nk由均匀分布U（0，20）随机产生，即Nk的均数为10［5-6］。

（2）随机效应及参数设置

假设随机效应uk来自正态分布，均数为0，方差为0.1或0.2两种情况，分别相当于类内相关系数在0.01和0.15之间，其大小依赖于暴露因素和协变量的效应。研究显示这种大小在实际资料中常见。

（3）固定效应及参数设置

固定效应x1ki为二分类变量，假定来自二项分布，即x1ki～B（p）；x2ki为连续变量，假定来自均匀分布，且依赖于x1ki，即x2ki/x1ki～U（-6＋2x1ki，2＋2x1ki）。考虑基线患病率为0.3和0.15两种情况，暴露因素X1的PR值分别为1.5和2.0，暴露率分别为0.2和0.5，协变量X2的回归系数分别为0.18，0.10，0.36和0.20［7］。共组成8种参数情况，如表1。

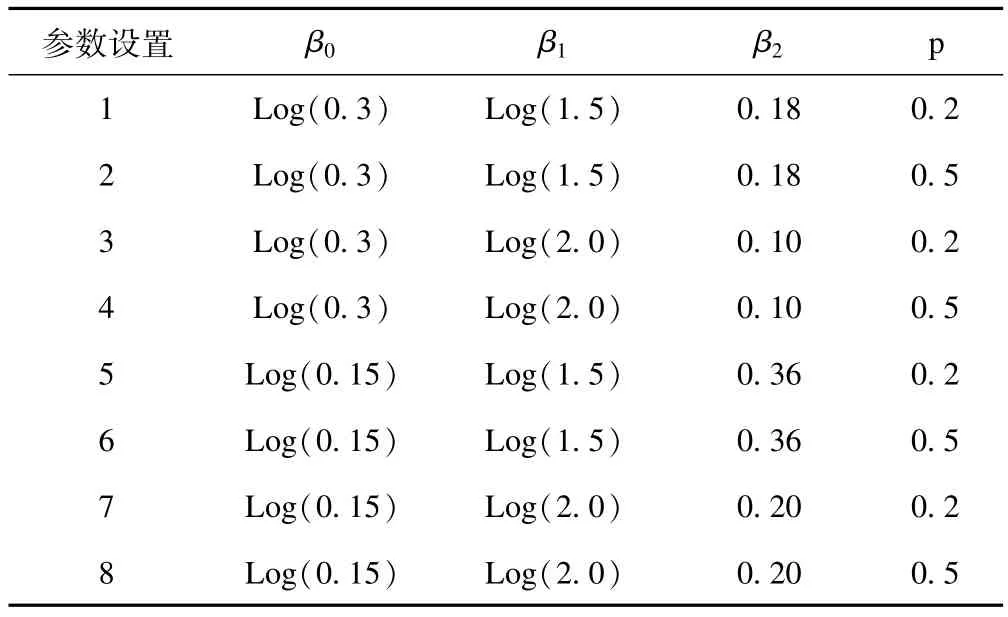
表1 模拟研究固定效应参数设置情况

（4）因变量Y的设置

两分类结局变量Y（1/0）来自n为1的二项分布，概率Pij为

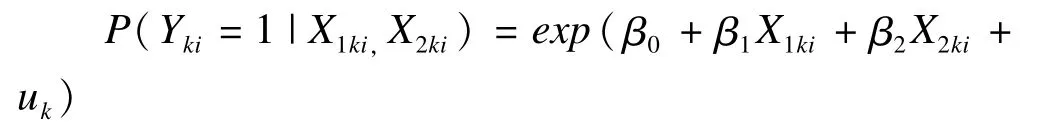
模拟过程中，如果固定效应和随机效应各组合的结果使Pki≥1，舍弃并模拟产生新的值，直到Pki＜1。

在上述各参数设置情况下，本研究共模拟2（类别数为20和50）×2（随机效应方差0.1和0.2）×8（固定效应参数设置情况1-8）＝32种情况。每种情况下，改变随机数的种子共模拟不相关的1000个数据集。所有模拟数据集均在SAS9.2软件中产生，并拟合稳健Poisson随机效应模型和Log-binom ial随机效应模型。

2.评价指标

（1）收敛率

对每种模拟情况，考察基于稳健Poisson、Log-binomial的两类随机效应模型的收敛情况并计算收敛率。

（2）参数估计值的均值和95%CI覆盖率

在每种模拟情况下，根据每种模型的1000个参数估计结果，分别计算回归系数β0，β1和β2估计值的均值及95%CI对参数真值的覆盖率。

3.结果

（1）收敛率

表2显示32种模拟情况下两类随机效应模型参数估计的收敛率（%）。32种模拟条件下稳健Poisson随机效应模型的收敛率波动范围为81.4%～ 100.0%，而Log-binomial随机效应模型的收敛率波动范围为4.7%～98.6%，波动较大。类别数为20时稳健Poisson随机效应模型和Log-binomial随机效应模型的最低收敛率分别为81.4%和5.9%；类别数为50时稳健Poisson随机效应模型和Log-binomial随机效应模型的最低收敛率分别为91.9%和4.7%。

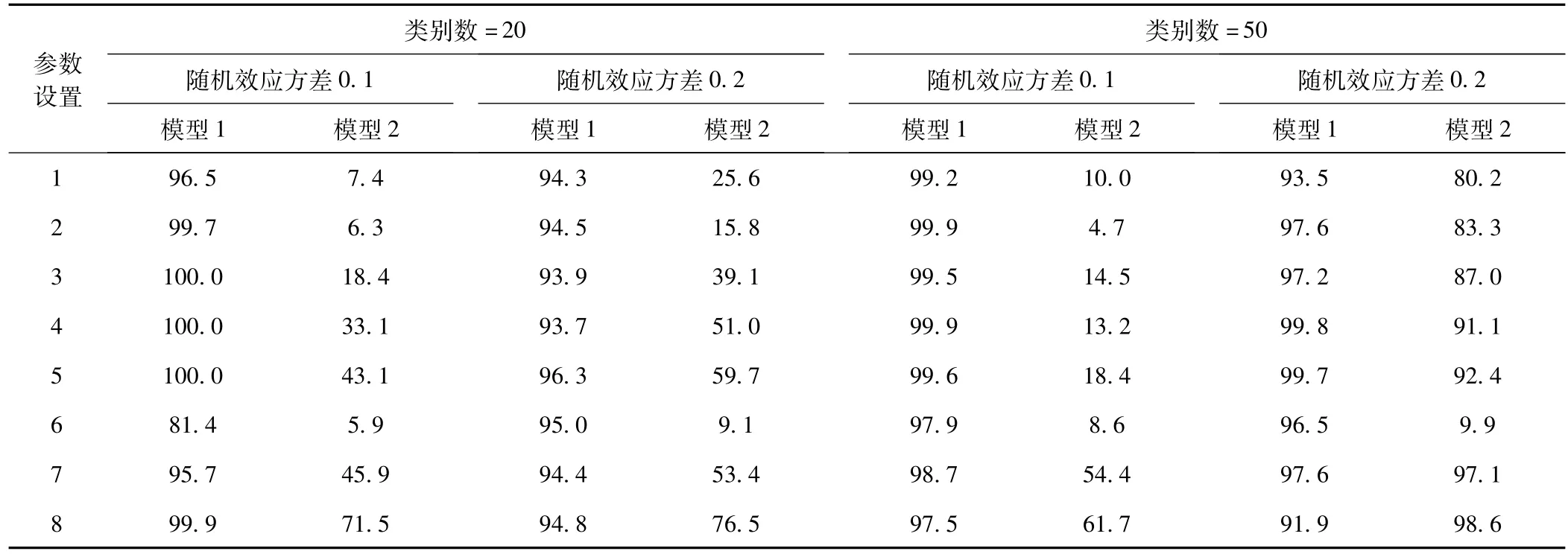
表2 32种模拟情况下两类随机效应模型参数估计的收敛率（%）

（2）参数估计值的均值与95%CI覆盖率

表3和表4显示了2类模型在不同随机效应方差水平、类别数及固定效应参数条件下分别进行1000次参数估计的β0、β1、β2的均值和95%CI覆盖率。两模型对各设定条件下的参数估计结果与真值均较为接近，受类别数或随机效应方差的影响不大。

稳健Poisson随机效应模型对各参数的覆盖率均在80%以上，和Log-binomial随机效应模型相比，95%CI覆盖率变异较小；在随机效应方差较小（0.1）时，稳健Poisson和Log-binomial的随机效应模型参数估计的95%CI覆盖率较接近，受类别数目影响较小；当随机效应方差增大和类别数同时增大时，Log-binomial随机效应模型估计的各参数95%CI覆盖率降低，且变异较大。

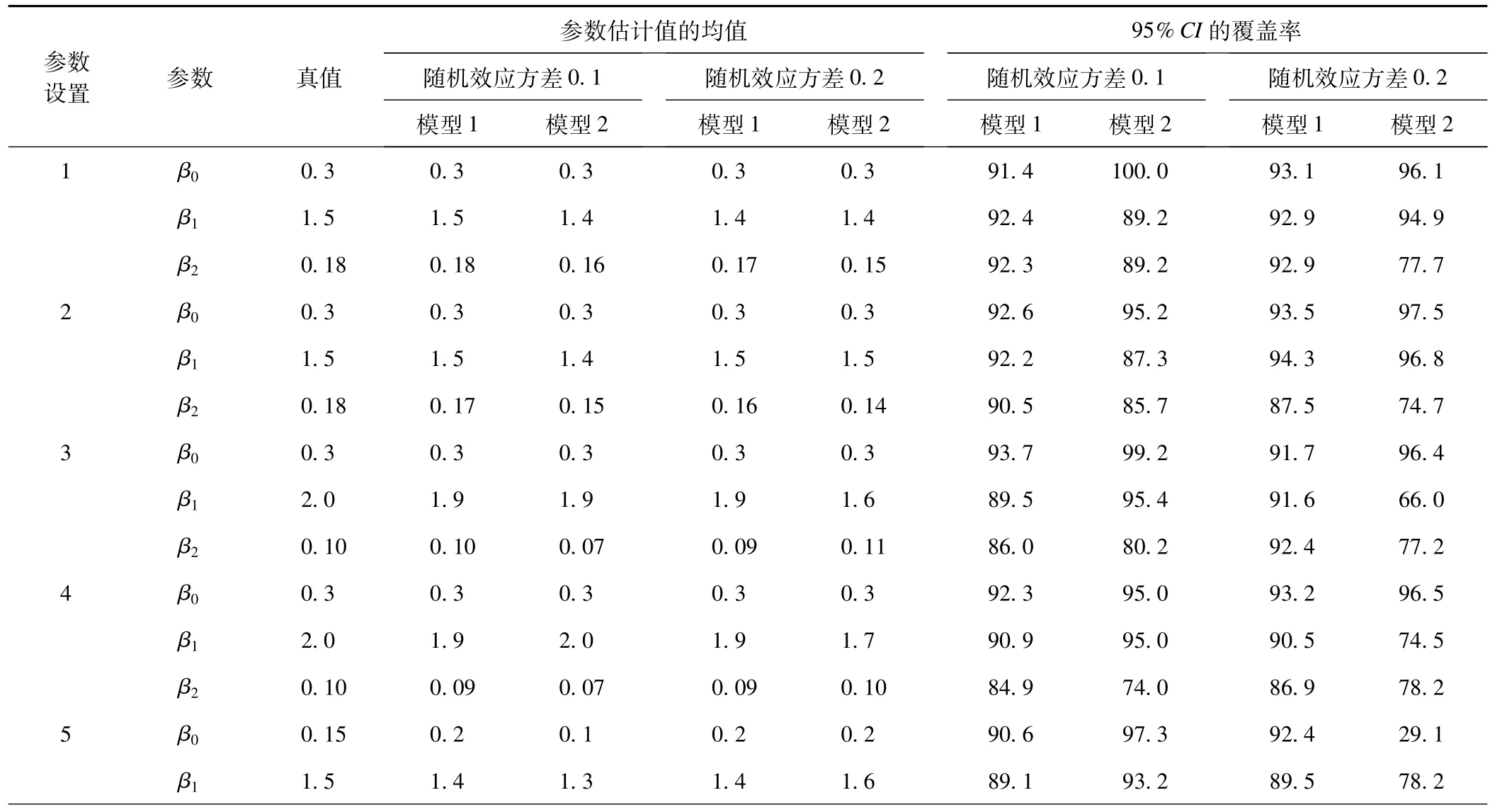
表3 类别数为20时，两种模型参数估计均值与真值的比较以及95%CI的覆盖率

*：模型1和模型2分别是稳健Poisson-随机效应和Log-binom ial-随机效应（COPY算法）

表4 类别数为50时，两种模型参数估计均值与真值的比较以及95%CI的覆盖率

讨 论

队列研究或横断面研究资料中，稳健Poisson回归和log-binom ial模型常用于估计RR/PR，当用于独立数据时，Deddens［8］显示中等样本量情况下，稳健Poission回归对PR估计的偏倚小于Log-binomial模型，但Log-binomial模型所估计的患病概率不会大于1，且可以使用似然比检验，相较Wald检验可能更好。但运用稳健Poisson模型几乎很少有收敛问题，又可直接对原始数据分析，省去了数据操作的过程而更容易使用，因此学者建议［9-10］，log-binomial不收敛时可首先考虑稳健Poisson回归。

另一方面，解决非独立数据的问题，很自然地思路是将其推广到多水平模型，因此本研究主要探讨Logbinom ial模型和稳健Poisson模型的随机效应模型，采用计算机模拟实验考察不同组合情况下模型参数估计的有效性和准确性。

本研究中的模拟实验共设置了32种参数情况，分别反映实际资料中的少数类别数和中等类别数，小强度和中等强度的类内聚集，模拟结果显示，各类参数设置情况下，两类随机效应模型的参数估计值与真值差别均不大，估计RR/PR有较高的准确性，且稳健Poisson随机效应模型的覆盖率较高。但随着类内聚集性增大，Log-binom ial的随机效应模型95%CI覆盖率变动较大，且类别数增加时覆盖率普遍较低，表明稳健Poisson随机效应模型的稳健性较好。此外Log-binom ial随机效应模型的收敛效果劣于稳健Poisson随机效应模型，这与独立数据时情况一致，在Log-binomial模型基础上增加随机效应后可能导致更多参数估计的不确定性。

尽管本研究不能穷尽各种可能的实际情况，但模拟条件下结果显示，和Log-binomial随机效应模型相比，运用稳健Poisson随机效应模型几乎很少有收敛问题，又可直接对原始数据分析，省去了COPY算法中数据操作过程而更容易使用；参数估计值与真值的绝对偏差均较小，对各固定效应参数估计的95%CI的覆盖率高且稳定，故在结局频率较高的非独立数据中估计RR/PR时推荐使用。不过Kauermann＆Carroll在实验中发现三明治方差的估计效率较基于模型的方差估计方法的差，尤其是当数据来源于小样本的实验单位而且不同实验单位间协变量不同时，主要表现为参数估计的置信区间覆盖率较低，此时建议对置信区间进行校正［12］。

1.Strömberg U.Prevalence odds ratio v prevalence ratio.Occup Environ Med，1994，51（2）：143-144.

2.Deddens JA，Petersen MR，Lei X.Estimation of prevalence ratioswhen PROC GENMOD does not converge.Proceedings of the 28th Annual SASUsers Group International Conference，Seattle，Washington，2003：270-28.

3.Deddens JA，Petersen MR.Approaches for estimating prevalence ratios. Occup Environ Med，2008，65（7）：501-506.

4.Savu A，Liu Q，Yasui Y.Estimation of relative risk and prevalence ratio.Stat Med，2010，29（22）：2269-2281.

5.Yelland LN，Salter AB，Ryan P.Relative Risk Estimation in Cluster Randomized Trials：A Comparison of Generalized Estimating Equation Methods.International Jof BIOST，2011，7（1）：1-26.

6.Yu B，Wang Z.Estimating relative risks for common outcome using PROC NLP.Comput Methods Programs Biomed，2008，90（2）：179-186.

7.Zou GY，Donner A.Extension of themodified Poisson regressionmodel to prospective studies w ith correlated binary data.Stat Methods Med Res，2013，22（6）：661-670.

8.Petersen MR，Deddens JA.A comparison of twomethods for estimating prevalence ratios.BMC Med Res Methodol，2008，8：9.

9.Lee J，Tan C S，Chia K S.A practical guide formultivariate analysis of dichotomous outcomes.Ann Acad Med Singapore，2009，38（8）：714-719.

10.Spiegelman D，Hertzmark E.Easy SAS calculations for risk or prevalence ratios and differences.Am JEpidem iol，2005，162（3）：199-200.

11.Goran K，Raymond JC.A note on the efficiency of sandw ich covariancematrix estimation.JAm Stat Assoc，2001，12：1387-1396.

（责任编辑：郭海强）

A Com parative Study between Robust Poisson and Log-binom ial M odel w ith Random Effects M odels to Estimate RR/PR in Non-independent Data

Zhou Shudong，Gao Yanhui，Li Lixia，et al（DepartmentofEpidemiologyandBiostatistics，SchoolofPublicHealth，Guangdong PharmaceuticalUniversity，GuangdongKeyLaboratoryofMolecularEpidemiology（510310），Guangzhou）

ObjectiveTo compare the parameter estimation results based on robust Poisson and Log-binomialmodels w ith random effects in the hierarchical and uncommon outcome datasets.MethodsThe simulation datasets were generated by computer，including 32 kinds of parameters conditions，respectively，reflecting the small and the medium number of categories，low and medium aggregation w ithin the classes，0.15 and 0.3 of the baseline prevalence，1.5 and 2.0 of the PR value，20%and 50%of the cases’exposure rate.The convergence rates，parameter estimation results and the 95%CIcoverage parameters in all the simulations were compared.ResultsThe convergence effects of Log-binom ialmodel w ith random effects were worse than the robust Poisson.The estimation results of two random effectsmodel were both closer to the true value.Two random effects models’95%CIcoveragewere good when the classes’aggregation was low，butw ith the addition in intra-class clustering，95% CI coverage of Log-binom ial random effectsmodelwas unstable，and the coverage was generally low when the number of categories increased.ConclusionThe convergence rates of robust Poisson random effectsmodel were good，the parameter estimation resultswere close to the true value，and the 95%CIcoverageswere high and stable，superior to Log-binom ial random effects model.

Non-independent；Robust Poisson regression；Log-binomialmodel；Random effects；Prevalence ratio

广东省自然科学基金（项目号：10151022401000018）

1.广东药学院公共卫生学院流行病与卫生统计学系，广东省分子流行病学重点实验室（510600）

2.Department of Epidem iology and Community Medicine，University of Ottawa.

△通信作者：郜艳晖，E-mail：gao_yanhui＠163.com