应用时间序列模型预测辽宁省麻疹疫情*

安淑一赵 卓郭军巧韩 悦吴 伟方 兴周宝森△

应用时间序列模型预测辽宁省麻疹疫情*

安淑一1，2赵 卓2郭军巧2韩 悦2吴 伟1方 兴2周宝森1△

目的应用时间序列模型预测辽宁省麻疹疫情，进一步做好麻疹防控工作。方法用eviews软件基于辽宁省2000-2012年麻疹月发病数进行建模。结果应用建立模型为ARIMA（1，0，2）（0，1，1）12，预测结果均方根误差为8.11，平均绝对误差为6.69，平均绝对百分比误差为6.25，希尔不等系数为0.093，协方差比例为0.932。结论应用ARIMA模型预测麻疹疫情，预测效果较好。

麻疹 时间序列 ARIMA 预测

麻疹是严重危害儿童健康的一种疾病，患病后易发生严重的并发症，它是由麻疹病毒引起的急性呼吸道传染病，主要经呼吸道传播，麻疹患者是该病唯一的传染源。在实施麻疹疫苗接种前，几乎每个儿童都难以幸免麻疹病毒的感染，随着麻疹疫苗的广泛应用，麻疹发病在全球得到极为有效的控制。2005年卫生部提出在全国范围内消除麻疹的要求，为了更好的做好麻疹防控工作，早日实现消除麻疹的目标，根据辽宁省麻疹发病历史资料，选用随机时间序列中ARIMA模型对辽宁省2000-2012年麻疹发病情况进行分析，并利用该模型对2013年上半年麻疹发病情况进行预测，以期进一步做好麻疹防控工作。

ARIMA模型是一种比较成熟的预测模型，但只适用于平稳时间序列，在实际问题中，许多时间序列并不近似为平稳时间序列，所以不能直接用均值为常数的平稳过程模型建模。但是可以通过处理产生一个平稳的新时间序列。若模型包含季节性成分，则使用乘积季节模型ARIMA（p，d，q）（P，D，Q）s模型建模。d和D为差分和季节性差分次数。其中p、q、P和Q分别表示连续模型和季节模型中的自回归阶数和移动平均阶数。s是季节周期。用B表示后移算子的乘积季节模型的数学形式［1］为

材料和方法

1.资料来源

2000-2012年辽宁省麻疹病例每月报告发病数，数据来源于中国疾病监测信息报告管理系统（即传染病网络直报系统）。

2.方法

用Excel2007，EViews 6.0软件进行数据处理与分析。ARIMA模型建模过程按4个阶段［2］进行：（1）序列平稳化：ARIMA的应用需要时间序列符合平稳性的要求；（2）模型的识别：主要是根据ACF图和PACF图的特征，提出可能的模型作进一步分析；（3）模型参数估计和模型诊断：对提出的模型进行参数估计和诊断，如模型不恰当，则回到第二阶段，重新选定模型；（4）预测应用：2000-2012年的数据用于建立模型，对2013年1-6月麻疹发病数进行预测，比较实际发病数进行验证。

结 果

1.序列零均值化

对2000-2012年期间麻疹发病数据做序列图（见图1），观察序列基本变化趋势，并对序列进行零均值化处理（见图2）。

图1 2010-2012麻疹发病数序列图

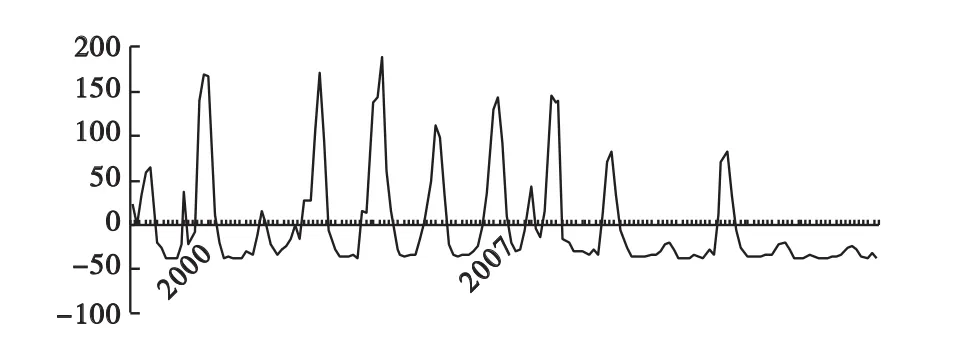
图2 2010-2012麻疹发病数序列图零均值化

2.序列的平稳化

一个平稳的随机过程应符合以下要求：均数不随时间变化；方差不随时间变化，自相关系数只与时间间隔有关，而与所处的时间无相关。上述序列图发现2000-2012年期间数据的变异程度较大，进行单位根检验（augmented dickey-fuller test，ADF），t值为-1.522，大于5%显著性水平临界值-1.943，判断为非平稳时间序列。

观察序列图，序列有明显的周期性，故对序列进行1次季节差分，再进行ADF检验，t值为-4.959，小于5%显著性水平的临界值-1.943，判断为平稳时间序列。

3.模型的识别与定阶

序列平稳化后，尝试建立ARIMA（p，d，q）（P，D，Q）12模型。12表示本季节模型以12个月为周期。上文已经对序列进行了1次季节差分，故d＝0，D＝1，目前模型为ARIMA（p，0，q）（P，1，Q）12。对于p、q、P和Q的确定，可以对序列做ACF图和PACF图（图3），ACF图呈正弦波，PACF图1阶后呈现拖尾。故q取1或2，p取1。季节模型的参数P、Q判断较为困难，但根据文献，参数超过2阶的情况很少见［3-5］，可以分别取0、l、2由低阶到高阶逐个试验，根据模型的AIC、SC、残差情况以及系数间的相关性进行综合判断。

考虑模型纳入各参数有统计学意义，且根据数据调整后的样本决定系数（Adjusted R2）、AIC准则与SC准则、考虑R2同时，选择AIC、SC最小时，拟合模型为最优模型。最后确定最优模型p＝1q＝2，P＝0，Q＝1。此时R2＝0.709，AIC＝9.418，SC＝9.501。模型为ARIMA（1，0，2）（0，1，1）12，（见表1）。

4.判断残差序列是否随机

本研究建立的ARIMA（1，0，2）（0，1，1）12模型，样本量为147，最大滞后期取12［6-7］，计算Q统计量Q12＝6.724，P＝0.567，判断残差为随机序列（见图4），模型可以应用。

图3 平稳序列的ACF图和PACF图

表1 模型各参数估计情况

模型数学形式为（1-0.348B）（1-B12）yt＝（1-0.523B-0.486B2）（1＋0.876B12）εt

5.预测

ARIMA（1，0，2）（0，1，1）12模型，预测结果均方根误差（RMSE）为8.11，平均绝对误差（MAE）为6.69，平均绝对百分比误差（MAPE）为6.25，希尔不等系数为0.093，协方差比例为0.932，表明模型预测结果较为理想［6-7］。

讨 论

应用模型对传染病的发病及流行强度进行预测预警有多种方法。流行控制图法、比数图法主要是根据发病率的大小和疫情发展的快慢，推测疾病发生或流行的趋势或强度。灰色动态模型GM（1，1）将原始序列累加、求均值而生成新的数列，使得GM（1，1）模型预测精度降低。利用人工神经网络（ANN）模型预测发病率，其难度在于确定网络结构，即如何确定隐含层的节点数；隐含层节点数太少，预测精度无法保证；节点数太多，又易陷入局部极小值，因此如何选择一个最佳的网络结构，成为一个关键问题。小波预测模型属于时间序列分析方法中的一种，预测精度可能稍高于ARIMA模型［8］，但计算步骤复杂，操作复杂。时间序列模型是基于预测对象本身的历史数据随时间发展变化规律建立数学模型而外推的预测方法［9-10］，在理论上时间序列模型已经有一套明确的准则，适用于各种复杂的时间序列模式，由于将拟合误差作为重要因素纳入模型中，故该模型预测精度较高。而且时间序列预测所需要的只是序列本身的历史数据，不需要对时间序列的发展模式作先验的假设，因此资料搜集整理简单易行，成本较低，而且可以通过反复识别修改，获得最满意的模型，因此在传染病预测预警上有很好的应用前景。

图4 残差的ACF图和PACF图

对辽宁省2000-2012年逐月麻疹发病数数据分析，发现辽宁省麻疹发病存在明显的季节性，每年3、4、5、6月高发，总体发病率不高，但发病波动较大，2008年后，发病下降明显，这与实际情况相吻合，也为麻疹季节性防控提供了依据。由于麻疹发病的影响因素很多，如人群易感性、卫生条件、流动人口、发生疫情后采取的控制措施、全国疫情形势及周边省份发病情况对辽宁省的影响等，这些因素都会对预测效果产生影响。本研究建立的ARIMA乘积季节模型，预测结果较好，可以作为指导疫情防控的参考资料。但也应该注意到，由于疫情波动受到诸多未知随机因素的影响，所建立的模型也不是一成不变的，它更适合进行短期的预测，同时需要不断添加新的实际值，以不断拟合更能反映实际情况的预测模型，并提高预测的敏感性。与一般时间序列模型相比，ARIMA模型需要更多的历史数据，当实际问题影响因素多，更加复杂时，模型的建立相对比较困难，应用者需理清思路、对实际资料有深刻的理解，并不断积累经验，才能获得更合适的模型。

1.孙振球.医学统计学.北京：人民卫生出版社，2010：390-403.

2.张蔚，张彦琦，杨旭.时间序列资料ARIMA季节乘积模型及其应用.第三军医大学学报，2002，24（8）：955-957.

3.赖圣杰，李中杰，金连梅，等.传染病暴发早期预警系统评价内容及其指标.中华流行病学杂志，2009，30（6）：637-640.

4.易丹辉主编.数据分析与EVIEWS应用.北京：中国人民大学出版社，2008：137-140.

5.胡建利，梁祁，吴莹，等.季节时间序列模型在菌痢发病预测中的应用.中国卫生统计，2012，29（1）：34-39.

6.宋廷山，刘贵基.基于Eviews软件的回归模型优选问题研究.统计教育，2007：23-25.

7.彭志行，陶红，贾成梅，等.时间序列分析在麻疹疫情预测预警中的应用研究.中国卫生统计，2010，27（5）：459-463.

8.吴学森，王洁贞，刘云霞，等.肾综合征出血热发病率的小波预测模型.中国公共卫生，2004，20（9）：1031-1033.

9.Brockwell PJ，Davis RA.Time series：Theory andmethods.2nd edition. NewYork：Springer-Verlag，1991.

10.陶芳芳，赵耐青，何懿，等.广义相加模型在细菌性痢疾预警中的应用.中国卫生统计，2012，29（4）：481-483.

（责任编辑：郭海强）

Forecasting M easles Epidem ic Situation by App lying the Time Series M odel in Liaoning Province

An Shuyi，Zhao Zhuo，Guo Junqiao，et al（DepartmentofEpidemiology，ChinaMedicalUniversity（110001），Shenyang）

ObjectiveTo analyze themeasles epidem ic situation by applying the ARIMA of the time seriesmodel，and provide scientific evidence for forecasting measles epidem ic.MethodsThe forecastmodel was set up based on 2000 to 2012 monthly data of the measles surveillance，in Liaoning province by ARIMA mathematics model of eviews software system.ResultsThemeasles time series of Liaoning province accord w ith ARIMA（1，0，2）（0，1，1）12model，and the rootmean square error was 8.11，themean absolute error was 6.69，themean absolute percentage error was 6.25，the theil inequality coefficient was 0.093，and the covariance proportion was 0.932，predicted result was good.ConclusionIt is practical to apply the approach of ARIMA model to predictmeasles epidem ic.

Measles；Time Series；ARIMA；Forecast

国家自然科学基金资助项目（30771860）；青年科学基金资助项目（81202254）

1.中国医科大学流行病与卫生统计教研室（110001）

2.辽宁省疾病预防控制中心

△通信作者：周宝森，E-mail：bszhou＠mail.cmu.edu.cn