基于进化博弈论的城中村改造策略研究——以政府主导模式为例

卢宗亮，汤惠君

（华南农业大学 公共管理学院，广东 广州 510640）

1 城中村改造概述

1.1 城中村改造

城中村改造是城市经济迅速发展的产物，城中村作为城市构成的一部分，其内部所存在的“脏、乱、差”现象严重制约了城市的发展。现阶段，我国已经进入城市化的加速期，在城市规划方面表现为人口增长与面积的迅速扩张，原来城乡结合部的村庄在城市扩张过程中逐渐被城市新建城区包围，进而在地理位置上成为城市的一部分，原来村庄的土地大部分被新建城区所占用，村民基本不再从事农业生产，但仍保留着农民的身份。由于我国长期实行的城乡二元户籍制度的影响，村内的社会经济结构、管理制度以及生活方式与城市存在着较大差异，成为城市中一个特殊地域“城中村”［1］。由于其土地是属于集体性质的，在拆迁、安置、补偿等方面都具有一定的难度，而政府、参与改造的开发商和村民，都是涉及其中的利益相关者，城中村改造成功与否，最终要视各利益相关者的利益分配方式是否合理而定。因此，在整个城中村改造的流程中，大约60%～70%的时间都是在谈判桌上度过的，可以看出，分析研究城中村改造中各方主体博弈的重要性。

1.2 国内研究现状

关于城中村改造收益分配主体的博弈研究，近年来国内已有部分学者给予了关注，其中，吕霁［2］（2008）运用博弈论构建了一个城中村改造的动态博弈模型，分析各个相关主体之间的

利益博弈机制等。高冉、高文杰［3］（2011）等运用了博弈论的基本原理，基于政府、开发商和村民等不同利益相关者及其利用目标，分析了各个博弈主体需要得到的合理利益。也有一些学者认为，现有的博弈研究大多是建立在博弈主体完全理性的假定前提下的非合作博弈研究［4］，在信息的处理、决策等方面均具有局限性，借助其理念，本研究以城中村改造为研究对象，从城中村改造的一个典型特例—政府主导模式出发，进行模型的建立。

1.3 城中村改造的政府主导模式

政府主导模式也称政府赎买模式，一般指基于城市建设的需要，政府按市场估价或双方协商一致的价格将村民所属集体土地及物业全部或部分赎买，村民在拿到足额补偿后，自行或由政府协助统一进行异地安置；其后，由政府或政府委托的开发商对腾空的旧村进行拆除，并按照城市建设的标准和项目用地的要求进行开发建设［5］。可见，政府和村民在改造中将围绕土地产权归属和既得利益的补偿展开博弈［6］。

这种模式有以下的特点：（1）对村民的土地和物业实行一次性买断，关系较为单纯，操作简单易行；（2）政府需支付高昂的赎买资金和安置成本；（3）由于容易发生补偿方面的争议、政府需付出较大成本以及对异地安置的村民未来生计难有妥善解决之策［7］。

这种模式主要适用于规模较小、地理位置较偏、经济实力较弱、机会成本（损失）不大的城中村，或涉及到国家重大工程项目需强制征用农村土地的情形。

2 进化博弈论与传统博弈论的区别

进化博弈论是在经济学中一种崭新的分析方法，相对于传统博弈论而言，其对于主体的要求、博弈的动态性问题、信息的处理和博弈的均衡均不相同，也更符合现实。

2.1 对于博弈主体的条件要求不同

相对于进化的博弈论，在传统博弈论下博弈主体具有更高的要求，博弈主体除了实现自身利益的最大化外，对于其他的博弈主体也具有完全的信任程度，深信对方的措施能够实现己方和对方的最大均衡。此外，博弈主体也必须具有较高的判断能力。在现实世界中，除非博弈方各方面的素质都比较完美才有可能实现，并且需要排除博弈主体以“经济人”角度提出的观点和采取的手段。

而进化博弈论更偏向“经济人”的角度，充分考虑到各方面的利益和诉求，不需要博弈主体具有较高的认知能力，也不要求博弈多方主体具有较高的信任程度，也保留了博弈方为了追求利益最大化时采取的手段因素等。对于城中村改造而言，由于各方的利益诉求都是比较强烈的，采用进化博弈论进行分析会更有说服力。

2.2 决策的时点性质不相同

传统的博弈论对于主体的决策判断力具有更高的要求，主要有两方面的表现：一方面，对于决策者本身的能力具有较高的要求，认为博弈主体具有较高的知识文化水平，能够迅速地制定多种的决策方案并且从中选出最优的方案并给出详细的论证。另一方面，传统博弈论没有考虑判断时机的重要性，尽管运用贴现方式消除时间的影响，但在贴现率的选取上也存在偏向性。

进化博弈论不要求博弈主体能够选择出最优决策，而是基于时间的基础上，不断进行多维的调整，直到最大的均衡为止，调整是一个复杂的渐进阶段，很大程度受决策时点的环境条件影响。

2.3 进化博弈论的自我学习特性

进化博弈论是居于有限理性的基础上提出的，考虑了人在处理问题上的局限性。首先，人的记忆力和判断能力是不可靠的，在面对各种情况时的反应速度也各有偏差；其次，在面对一些切身的利益问题时，往往容易失去理性，在城中村改造中，村民的表现尤其明显。而进化博弈论充分肯定了人的模仿能力和学习能力，认为人都是聪明的，能通过模仿和总结经验，从错误和失败中学习正确的的做法，逐步成为赢家。

传统博弈论则忽略了人在处理问题的局限性，认为人具有高度的决策能力，面对各种情况均可以采取最佳的判断，而不需要有一个循序渐进的过程。

2.4 进化稳定策略均衡的先进性

进化稳定策略是生物学提出的，指种群的大部分成员所采取某种策略，这种策略的好处为其他策略所不及。人与人之间常常为各种利益竞争或合作，但竞争或合作不是杂乱无章的，而是按一定的策略进行的。由于人是“社会人”，在获取自身的利益过程中不能忽视周边群体的存在和影响，一旦某个个体为了追求自身的利益而实施的策略与周边群体相违背时，必然与周边群体引发冲突，这种冲突也必然导致双方利益的下降。为了自身的利益，个体和群体将会在不断的冲突中调和，随着冲突的次数越多，双方的磨合程度也就越高，最后，个体将会服从群体的策略，也就是进化稳定均衡。

传统博弈论最终的博弈结果是纳什均衡，但是一旦主体数量增多时，情况就变得复杂，低维度的博弈模型也无法演绎多重主体的均衡问题。

3 需要解答的问题

在采取政府主导模式进行城中村改造的过程中，政府和村民就是博弈的两方主体，然而，双方的行为意识、分析推理能力、判断能力和记忆能力等具有重大差异，基于传统的博弈理论分析是不科学的。政府侧重的是城市建设、改善市容等方面，自然希望改造的成本越低越好，或者通过建立一个体系以达到削减成本的目的。村民方面希望能够获取更多的利益，一般难以认同政府以市场价进行补偿。因此，双方开始形成一个“冲突—谈判”的过程，通过不断学习、不断进化达到均衡。通过以进化博弈论对两者的博弈过程进行分析，建立相应的模型，即可得出使两者均衡的最佳决策。

4 城中村改造进化博弈模型的建立

4.1 改造过程中监控指标的量化表示

假定政府在采取政府主导模式进行城中村改造，双方总共投入成本为S，其中政府投入的比例为α（0＜α＜1）主要为政府的赎买资金、安置成本、谈判成本和时间成本等。村民投入的比例为β（0＜β＜1），主要为村民所持有房屋的价值在货币上的表现，以及在改造过程中所损失的机会成本。α＋β＝1，所以政府的投入成本为αS，村民的投入成本为βS。

双方在投入后获得一个共同收益，政府可以获得由于土地价值提升所带来的税收收益、相关收益以及无形收益，村民则直接获得货币收益。这些收益最终都能在货币上直接体现，形成一个共同总收益E。假定投入的比例直接决定收益的比例，那么在此过程中，政府的收益为Eg＝αE，村民的收益为Ev＝βE。

假定城中村改造中所有的积极影响均转化为净收益，所有的消极影响转化为成本。则城中村改造可以理解为一项投入产出行为，两者可以通过投入产出率I（投入成本与收益的比值，0＜I＜1）转化。则S和E的关系可以表示为E＝S/I，根据规模效应原理，一个项目的收益是有极限的，当达到了这个极限，就算加大投入也不能再增加项目收益，为了获得这个收益，必须当前具有一个较好的投入产出率，当这个投入产出率越大，投入的成本也就越大，规模越不经济，因此投入产出率与投入成本是一个正比例的关系。而E是一个最优目标值，为常数。

而城中村的改造成本是受工作绩效影响的，此工作绩效与政府的知识能力、判断力、决策力以及村民的配合程度有关，工作绩效越大，所需要的改造成本也就越小，两者成反比例关系。设工作绩效系数为K（0＜K＜1），则改造成本与工作绩效系数的关系为S×K＝1。综合上述两式求解得：I＝（E×K）－1

进化博弈论要求博弈主体必须通过多次的协商以降低交易成本，当经过多次的谈判、磨合和协商，也就是说，必须使K尽量向1趋近，为了考虑协商次数的问题，以（1＋K）n＋1取代I＝（E×K）－1式中的K值，K的含义不变，n为协商的次数，经过变换，可转化为：I＝［E（1＋K）n＋1］－1。

如果不进行相互的学习、协商、改进（n＝0），由于（1＋K）n＋1的取值为最小值1＋K，为了获得最优目标收益E所付出的成本也就越大（投入产出率为［E（1＋K）］－1），随着时间的发展，双方的学习次数越多，投入产出率也就越小，成本也就越小。

4.2 政府主导模式中政府和村民的博弈关系

对于博弈的双方而言，为了追求共同的目标E，均有两个选择：对于政府而言，政府可以不断提高自己的知识能力、判断能力和决策能力，推进城中村改造，记此策略为G1。也可以维持当前的决策手段以避免成本支出，记此策略为G2。对于村民而言，村民可以采取一定程度的抵触以提高自身的收益分成，但会增加投入成本，记此策略为V1。也可以选择积极配合政府的任何决定，减少成本，记此策略为V2。

在此过程中，政府和村民的选择都是有限理性的，因此各种策略的出现均具有随机性。对于政府而言，选择G1的概率为p，选择G2的概率为1－p。对于村民而言，选择V1的概率为q，选择V2的概率为1－q。

根据上述的假设和博弈策略，可得到策略矩阵如图1：

图1 政府和村民的策略矩阵

4.3 不同策略组合博弈主体的净收益分析

由上述博弈矩阵可见，在政府主导模式下的城中村改造有四种决策组合，分别是（G1，V1），（G1，V2），（G2，V1），（G2，V2）。在不同组合下，政府和村民的收益分析如表1所示：

表1 政府与村民的收益分析

由于城中村改造是由政府发起的，政府具有选择策略的先行性，而根据村民所持的态度所得到的收益分成也不相同。

①当政府采取G1策略时，所得到的期望收益如下：

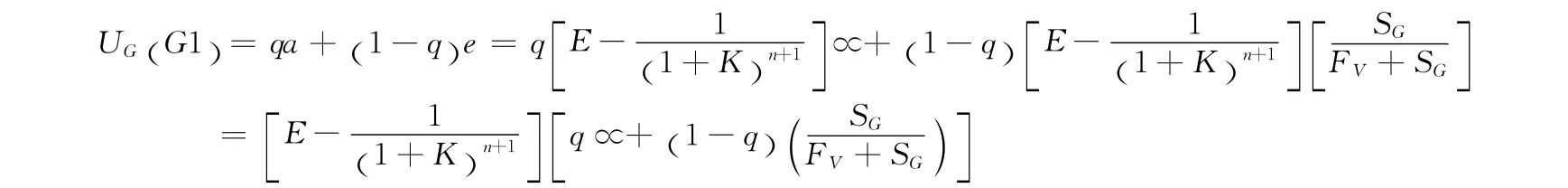
②当政府采取G2策略时，所得到的期望收益如下：

③当村民采取V1策略时，所得到的期望收益如下：

④当村民采取V2策略时，所得到的期望收益如下：

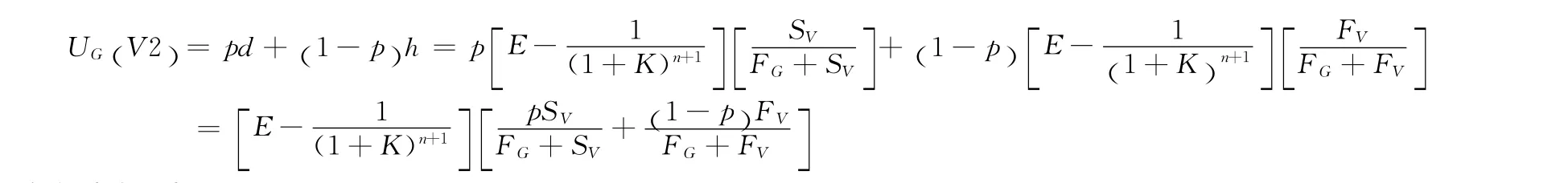
4.4 均衡动态分析

4.4.1 政府的进化稳定策略分析

基于进化博弈论的原理考虑，受各种因素的影响，政府决策者群体中持不同政策意见的成员比例会不断发生变化。随着采取积极政策人数的增多，所获得的期望收益也就越多，根据动态微分方程定理，政府的复制动态方程如下：

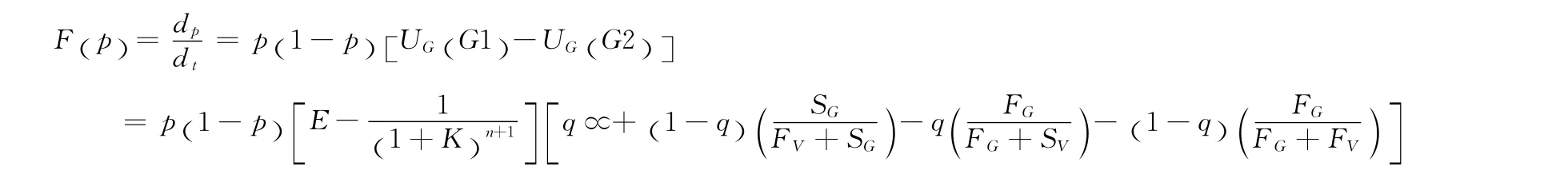
上述方程的阐述了决策人数的增长比例随决策水平变化而变化的状况，如果政府不断地学习、不断地提高知识水平和决策能力，采取积极手段的人数比例也就越大，增长速度越快。式F（p）在 ［0，1］区间内，局部均衡点有两个，分别为p＝0，p＝1。当p＝0时，表明支持积极策略的决策者人数不再增加，达到了均衡。对动态方程的分析如下：

由于p＝0，p＝1是两个比较特殊的均衡状态，属于均衡过程的起始和终结，而进化博弈的均衡要求体现在均衡的过程中，即具有抗扰动的性质［3］（2010）。对政府的复制动态方程求导，得：

此时，当q＝q0时，F′（p）＝0，因此不存在进化稳定策略；当q＞q0时，δ＞0，可知只有q＝1是进化稳定策略；当q＜q0时，δ＜0，可知只有q＝0是进化稳定策略。

4.4.2 村民的进化稳定策略分析

村民的情况也与政府相仿，根据微分方程定理，村民的复制动态方程如下

此时，当p＝p0时，F′（q）＝0，不存在进化稳定策略；当p＞p0时，θ＞0，只有p＝1是进化稳定策略；当p＜p0时，θ＜0，只有p＝0是进化稳定策略。

4.4.3 总体的进化稳定均衡分析

上述两者的均衡状态可以用下图表示：

图2 政府和村民的均衡状态

由图2看出，在此博弈模型中，p＝0，p＝1，q＝0，q＝1都是进化稳定策略的起始和终结状态。A表示可变化的均衡状态点，一般来说，A点起初将会落在（G2，V2）区，且本区的面积较大，随着双方的不断学习，不断改进，p0线不断向右移，q0线不断向上移，压缩（G2，V2）区面积，从而增大（G1，V1）区的面积，达到最优。

5 研究结论

综上所述，进化博弈论能揭示政府和村民“政府主导模式下”的一个双向学习过程，为推进城中村改造提供了一个较新的分析方法。

［1］黄建清.欠发达地区“城中村”改造适应模式和对策研究：以浙江省丽水市“城中村”改造为例［D］.杭州：浙江工业大学，2010.

［2］吕霁.基于博弈论的城中村改造模式研究［D］.武汉：华中师范大学，2008.

［3］高冉，高文杰，张兰兰，等.城中村改造中的博弈关系分析与应对［J］.安徽农业科学，2011，39（12）：7489－7491.

［4］张侠，赵德义，朱晓东，等.城中村改造中的利益关系分析与应对［J］.经济地理，2006，26（3）：496－499.

［5］董玉晶.基于博弈论的城中村改造研究［D］.济南：山东大学，2012.

［6］唐忠义，姚科敏.城中村改造中的博弈关系与战略选择［J］.湖北社会科学，2009（3）：32－34.

［7］黄静晗.城中村改造中的多元主体利益关系分析：基于场域理论视角［J］.中国集体经济，2010（12）73－74.

［8］刘家瑛.政府在城中村改造中的作用研究：以西安市城中村改造为例［D］.西安：西北大学，2009.