三次平面H-Bézier螺线

蔡华辉， 柳炳祥， 程 燕

（1. 景德镇陶瓷学院信息工程学院，江西 景德镇 333000；2. 景德镇陶瓷学院设计艺术学院，江西 景德镇 333000）

三次平面H-Bézier螺线

蔡华辉1， 柳炳祥1， 程 燕2

（1. 景德镇陶瓷学院信息工程学院，江西 景德镇 333000；2. 景德镇陶瓷学院设计艺术学院，江西 景德镇 333000）

基于光顺曲线设计需求，一条曲率单调且曲率正负不变的三次平面H-Bézier螺线段被构造。由于此螺线具有起点曲率为零的特性，它可以替代回旋曲线作为道路设计中的缓和曲线。同时螺线还含有形状参数，故它具有曲线形状可调性的优点。最后，利用此H-Bézier螺线，构造了两直线间满足G2连续的缓和曲线。

H-Bézier螺线；单调曲率；缓和曲线

螺线，是曲率恒正或恒负，且曲率单调变化的平面曲线[1]。由于螺线在曲线内部不包含曲率极值点、拐点，它非常适合轨道路径设计、曲线光顺等工程应用。例如欧拉螺线，即回旋曲线，具有曲率和弧长成比例的优美特性，在道路轨道设计[2]和物体轮廓缺失边界的修复[3]等领域都有大量应用。尽管Bézier多项式曲线在计算机辅助几何设计(CAGD)中被广泛地使用，但其曲率单调性判别是困难的， 因此许多学者提出构造多项式螺线用来设计光顺曲线。Mineurl等[4]提出了一类单调的多项式曲线，但其没有拐点（曲率为零点），这大大限制了它的作用。Walton和Meek[5]模仿欧拉螺线，提出了一条起点曲率为0的三次Bézier螺线段，同时利用这条三次螺线替代欧拉螺线作为道路设计中的缓和（过渡）曲线，取得了良好效果。后来，Walton和Meek[6-7]推广三次螺线用于G2Hermite插值。Habib和Sakai[8-9]也对多项式螺线进行了广泛研究。Yoshida等[10-11]推广欧拉螺线曲率和弧长成比例的特性为曲率对数与弧长成比例，设计了一类用超越函数表示的

曲线：Log-aesthetic curves(LACs)，用于汽车轮廓和字体设计取得了良好的效果。

另一方面，为了克服Bézier曲线不能精确表示双曲线、悬链线等超越曲线的弊端，许多学者提出了不同函数空间的类Bézier曲线。Zhang[12]提出了基于空间的三次C-Bézier曲线，Chen和Wang[13]把它推广到任意高阶。在空间中，Wang和 Yang[14]提出了三次 H-Bézier曲线，王媛和康宝生[15]把它推广到任意高阶，檀结庆等[16-17]讨论了H-Bézier曲线的降阶、拼接等算法。这些类Bézier曲线充分显示出其既能统一表示自由曲线与悬链线等超越曲线，又有通过变动参数因子来调节形状的优越性与应用潜力。为了便于类Bézier曲线用于缓和曲线和光顺曲线设计，研究类Bézier螺线段的构造及其应用是十分必要的。蔡华辉和王国瑾[18-19]构造了一条含参数的三次C-Bézie螺线并应用与道路设计，但一直以来，三次H-Bézier螺线的构造方法一直没有给出。

1 三次H-Bézier螺线

以Zi(t) 为基，以qi(i=0,1,2,3) 为控制顶点的三次H-Bézier参数曲线形式如下所示[14]：

式中：

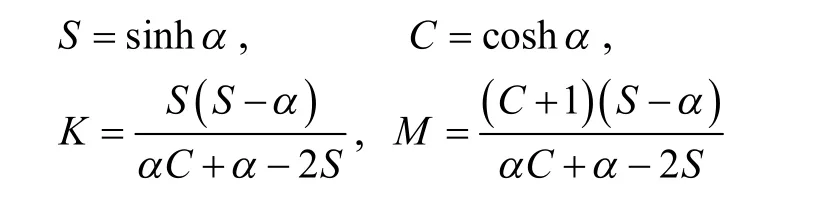
显然，K和M满足利用式(2)，三次H-Bézier曲线 Qα(t)的导数可表示为

下面给出平面三次 H-Bézier螺线的构造方法：

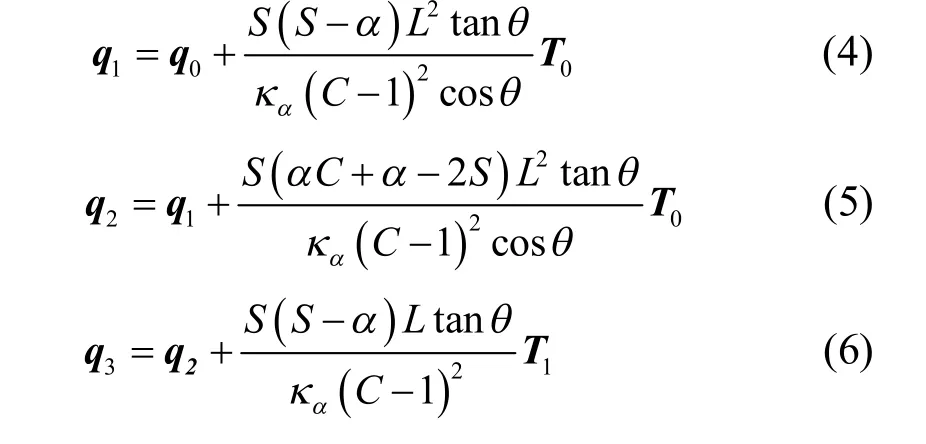
定理1.形如式(1)的平面H-Bézier曲线，若其控制顶点满足下列约束：式中，T0，T1分别是曲线首末端点的单位切向量，θ（0〈θ ＜π/2）为T0到T1的有向转角，κα为终点处的曲率，L满足

则H-Bézier曲线 Qα(t)的有向曲率 κ（ t）满足：

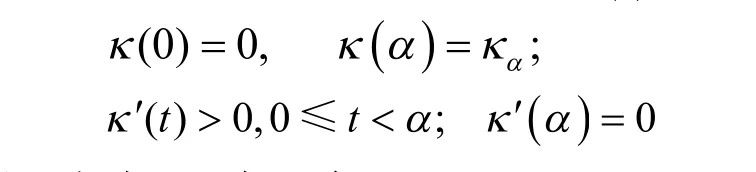
证明：由式(3)～式(6)有

则曲线有向曲率

式中：

再计算 κ（ t）的导数，利用数学软件Maple整理得：

式中：

由于 cosht在 t≥ 0单增，易判定0 ＜ t＜ α时gi（t） ＞ 0,（ i= 0,1），则故在0 ＜ t ＜ α内 κ′(t) ＞ 0,再把 t = 0,α代入式(7)、式(8)，可证定理。

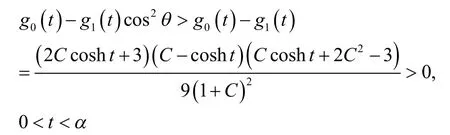
可以看到，在形状参数α确定以后，定理1确定的起点为0的H-Bézier螺线，实际上有5个自由度：起点P0的2个坐标，起点单位切向量T0, T0到终点单位切向量T1转角θ，以及终点处曲率κα。其他3个控制顶点可由这5个自由度通过式(4)～(6)求出。同时由于三次 H-Bézier曲线在α →0是三次Bézier曲线，且当α→0时，有所以，定理1中定义的H-Bézier螺线当α →0时就是Walton和Meek[5]中定义的三次Bézier螺线段。且当α＞0时，K/S＞1，所以q1是在q0q2上靠近q0一侧，这与C-Bézier螺线[18]是相反的。

图1给出了H-Bézier螺线的例子，点线表示α=3的 H-Bézier螺线，虚线是α=2的 H-Bézier螺线，实线是α→0时的三次Bézier螺线。

图1 三次H-Bézie螺线

在文献[5,18]中，分别利用 Bézier螺线和C-Bézier螺线替代回旋曲线作为直线和圆弧之间的缓和曲线。很自然地，此中方法也可以推广到H-Bézier螺线，并且α 可做为形状参数来控制缓和曲线的形状。由于利用H-Bézier螺线设计缓和曲线与C-Bézier的方法[18]非常类似，因此，下面只讨论两直线间的缓和曲线的构造方法，其他几类缓和曲线构造在文中不加以详述。

2 两直线间的缓和曲线

定理2.如图2，给定平面上不共线的三点P0, P,P1，则直线P0P,P1P单位方向向量及其夹角分别为

再令

式中：对κα＞0的任意常数，存在一对三次H-Bézier螺线

式中：

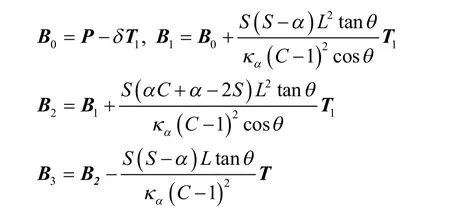
这对三次 H-Bézier螺线 Aα(t),Bα(t)满足在起点处分别与直线 P0P,P1P光滑 G2接触，且Aα(α) =B (α)，在端点处曲率的绝对值都为κα。证明：由于两条螺线的首个控制顶点 A0,B0分别在直线 P0P,P1P上，可设

α由图2可知，曲线 Aα(t)起点切向量T0和端点切向量T的有向转角是式(9)所给的θ，则 Bα(t)起点切向量T1和端点切向量T的有向转角为-θ。不妨设 Aα(t)在终点处的曲率为κα, 于是 Bα(t)在终点处的曲率就是-κα。设N是与端点切向量T成右手系的法向量，则

由定理1和式(11)，可得

再利用式(12)，上式可化为

同理可得

由于 Aα(α) =Bα(α)，则由上面两式可得式(10)，因此定理得证。

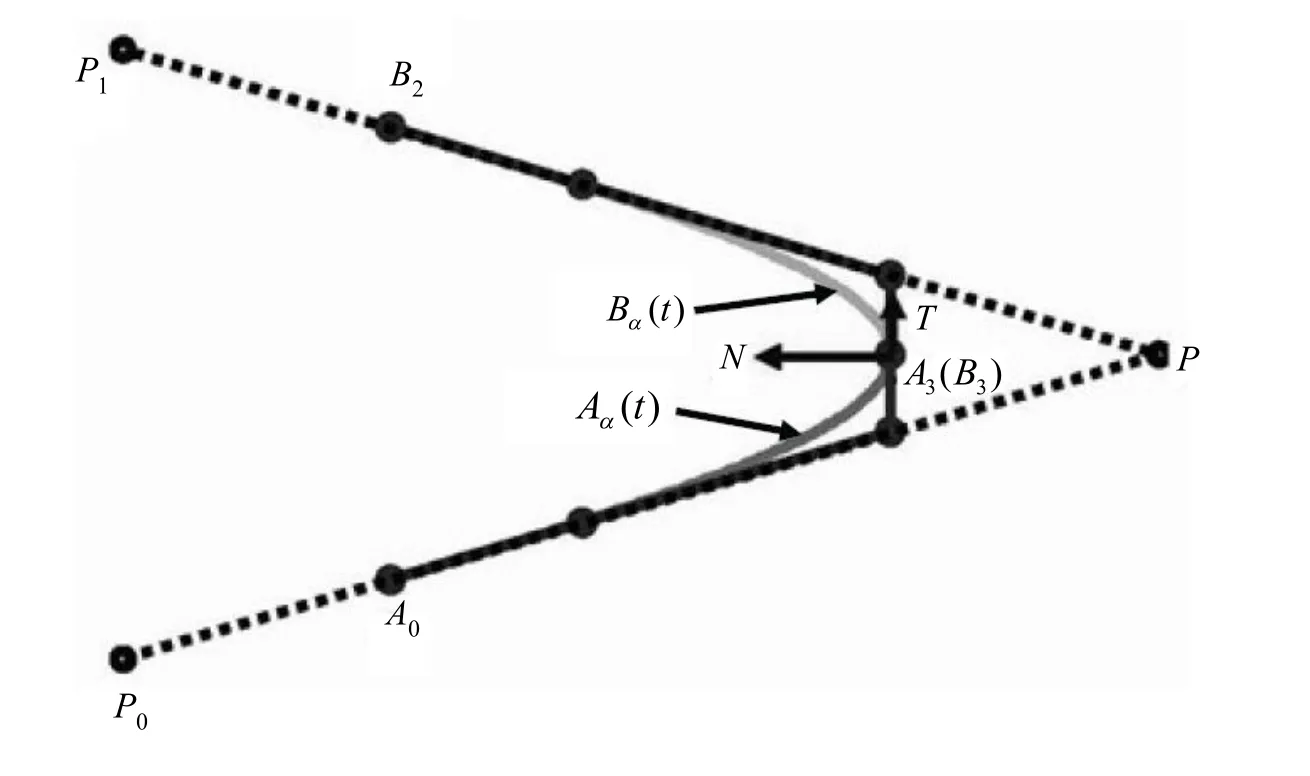
图2 两直线间的一对H-Bézier螺线过渡

3 结 束 语

本文构造了一条起点曲率为零的含形状参数α的平面三次H-Bézier螺线段。这条螺线段可以替代传统的回旋曲线，在路径设计等领域作为直线与圆弧之间的缓和曲线，并且还具有在保持曲率单调性不变的前提下，可通过形状参数α微调曲线形状的优点。但是，缓和曲线不是两点间 Herimite插值曲线。因此，利用三次H-Bézier螺线段研究 Herimite插值是今后值得研究的一个问题。

[1] Guggenheimer H W. Differential geometry [M]. New York: Dover Publications, 1977: 48-53.

[2] Fleury S, Soueres P, Laumond J P, Chatila R. Primitives for smoothing mobile robot trajectories [J].

IEEE Transactions on Robotics and Automation, 1995, 11(3): 441-448.

[3] Kimia B B, Frankel I, Popescu A-M. Euler spiral for shape completion [J]. International Journal of Computer Vision, 2003, 54(1-3): 159-182.

[4] Mineur Y, Lichah T, Castelain J M, Giaume H. A shape controled fitting method for Bézier curves [J]. Computer Aided Geometric Design, 1998, 15(9): 879-891.

[5] Walton D J, Meek D S. A planar cubic Bézier spiral [J]. Journal of Computational and Applied Mathematics, 1996, 72 (1): 85-100.

[6] Walton D J, Meek D S. Curvature extrema of planar parametric polynomial cubic curves [J]. Journal of Computational Applied Mathematics, 2001, 134(1-2): 69-83.

[7] Walton D J, Meek D S. A further generalisation of the planar cubic Bézier spiral [J]. Journal of Computational and Applied Mathematics, 2012, 236: 2869-2882.

[8] Habib Z, Sakai M. Transition between concentric or tangent circles with a single segment of G2 PH quintic curve [J]. Computer Aided Geometric Design, 2008, 25(4-5): 247-257.

[9] Habib Z, Sakai M. Admissible regions for rational cubic spirals matching G2 Hermite data [J]. Computer-Aided Design, 2010, 42(12): 1117-1124.

[10] Yoshida N, Saito T. Interactive aesthetic curve segments [J]. Visual Computer, 2006, 22 (9): 896-905.

[11] Ziatdinov R, Yoshida N, Kim T. Analytic parametric equations of log-aesthetic curves in terms of incomplete gamma functions [J]. Computer Aided Geometric Design, 2012, 29(2): 129-140.

[12] Zhang Jiwen . C-curves: an extension of cubic curves[J]. Computer Aided Geometric Design, 1996, 13(3):199-217.

[13] Chen Qinyu, Wang Guozhao. A class of Bézier-like curves [J]. Computer Aided Geometric Design, 2003, 20(3): 29-39.

[14] Wang Guozhao, Yang Qinmin. Planar cubic hybrid hyperbolic polynomial curve and its shape classification [J]. Progress in Natural Science, 2004, 14(1): 41-46.

[15] 王 媛, 康宝生. 代数双曲混合H-Bezier函数及其性质[J]. 西北大学学报(自然科学版), 2006, 36(5): 693-697.

[16] 檀结庆, 王 燕, 李志明. 三次H-Bézier曲线的分割、拼接及其应用[J]. 计算机辅助设计与图形学学报, 2009, 21(5): 584-588.

[17] 王 燕, 檀结庆, 李志明, 白 天. H-Bézier曲线的降多阶逼近[J]. 计算机辅助设计与图形学学报, 2011, 23(11): 1838-1843.

[18] 蔡华辉, 王国瑾. 三次 C-Bézier 螺线的构造及其在道路设计中的应用[J]. 浙江大学学报(工学版), 2010, 44(1): 68-74.

[19] Cai Huahui, Wang Guojin. A new method in highway route design: joining circulararcs by a single C-Bézier curve with shape parameter [J]. Journal of Zhejiang University Science A, 2009, 10(4): 562-569.

A Plane Cubic H-Bézier Spiral

Cai Huahui1, Liu Bingxiang1, Cheng Yan2
(1. School of Information Engineering, Jingdezhen Ceramic Institute, Jingdezhen Jiangxi 333000, China; 2. School of Art & Design, Jingdezhen Ceramic Institute, Jingdezhen Jiangxi 333000, China)

Based on the requirement of fairing curves design, a planar cubic H-Bézier spiral with monotone curvature of constant sign is discussed. Since this spiral segment has zero curvature at the beginning point, it is suitable for applications such as highway design where the clothoid has been traditionally used. And since the spiral also contains a shape parameter, it has the advantage of adjustable curve shape. Finally, G2continuous transition curves between the two lines are constructed by the use of the H-Bézier spirals.

H-Bézier spiral; monotone curvature; transition curve

TP 391

A

2095-302X (2014)03-0374-05

2013-10-23；定稿日期：2013-12-25

国家自然科学基金资助项目（61262038, 61164014）；江西省自然基金资助项目（2012BAB201044）

蔡华辉（1975-），男，浙江东阳人，副教授，博士。主要研究方向为计算机辅助几何设计与计算机图形学。E-mail：huahuicai@gmail.com