一种新型诊断技术在电机故障诊断中的应用

何银光

（克拉玛依职业技术学院，新疆 克拉玛依833699）

0 引言

在当前市场经济发展的过程中，电机对于我国现代工业生产活动的开展有着至关重要的影响，其是提供动力的主要构件。而在实际应用过程中，电机意外停机必然导致巨大的经济和社会损失。基于此，我们必须从当前的实际情况出发，探索出一套更为行之有效的方式方法，来保障电机系统运行的稳定性。当前较为常见的诊断方法包括小波诊断、遗传算法以及本文所介绍的神经网络算法等，已经有了较为成熟的应用案例。

多传感器信息融合作为当前阶段信息处理技术的主要发展方向，主要是通过对多传感器所提供的互补数据以及冗余数据的科学处理而反映所处时间和空间特征的一种诊断技术，其在实际应用过程中具有较大的实用价值。所以在本文的研究中，将该方法和原有的蚁群神经算法有机结合，希望能够使新算法在具有全局收敛特点的同时，可有效利用多源信息，从而为电机故障诊断工作的开展提供更为有效的数据支持。

1 新技术原理分析

作为一种应用范围相对广泛的复杂旋转机械，电机在实际应用过程中故障种类繁多，且难以通过直观的方式方法判断出来。实际上，电机故障不仅仅包括了机械故障所具有的各种共性，同样也有着时变、突发特征，因此在实际诊断过程中，准确判断故障原因相对比较困难。而如果采用单一神经网络模型来对故障进行判断，那么必然严重受模型本身质量的影响，因此引入蚁群神经网络就有了重要的现实意义。实际上，通过蚁群算法来对获得的多元数据进行分析和整理，能够有效地求得网络的可信任分配函数，然后以此为基础，在证据理论的指导下进行有效融合，就能够有效地为故障诊断工作的完成提供必要的数据支持。

2 新技术算法分析

2.1 蚁群神经网络

从本质上来说，本文中所引用的蚁群算法实际上是一种具有全局性特征的寻优算法，在实际应用过程中表现出明显的易于配合其他方法、较强的鲁棒性等特征。不过，传统的蚁群算法也同样表现出明显的问题，主要集中在搜索时间过长、容易陷入局部最小值等方面。为了克服上述问题，最小蚂蚁系统和最大蚂蚁系统的概念应运而生，即通过对最初信息设限的方式来保证算法不轻易陷入最小解。

本文中所引用的蚁群神经网络算法核心流程如下：首先完成对BP神经的界定；然后确定网络阈值和权值，并通过对蚁群算法的应用来求解两者的最优值；最后以所得到的最优解设定为该网络的初始权值和初始阈值，通过大量的网络学习来得出最终结果。

2.2 初始化系统

首先定义参数为神经网络的权值和阈值Pa＝｛wi｜wi为网络的权值和阈值｝，再将wi设置为N 个较小的随机非零值，形成集合Iwi，Iwi＝｛wij｜wij∈［－1，1］｝。i为网络权值和阈值的总数。每个参数的取值wij都对应信息素τij，定义信息素的值域范围是［τmin，τmax］，超过这个范围的值被限制为信息量允许值的上下限。在初始时刻，每个元素的信息素量相等，并设为信息素上限τ0＝τmax，初始信息素的增量为0。

2.3 适应度评价

在完成单次循环之后，需要对比适应度函数来对其中的信息素进行处理，在本研究中主要采用BP神经网络均方误差作为此函数，被选择元素优劣程度和均方误差值之间呈反比例关系。

2.4 元素选取规则

蚂蚁搜索时，每只蚂蚁从集合Ip1开始，依次遍历这N个集合，根据集合中每个元素的信息素按公式（1）选择一个元素。

各个蚂蚁在一次循环后，只有找到最优解的蚂蚁才能够在其经过的路径上利用公式（2）对信息素进行更新。

2.5 合成证据

证据理论是建立在一个非空集合辨识框架Θ上的理论，Θ由一系列互斥且穷举的基本命题组成。对任意命题A，均应属于幂集2Θ。在2Θ上，若函数m 满足2Θ→［0，1］，且满足：

如果A为Θ的子集，且m（A）＞0，那么在这一过程中我们就可以将其称为证据的焦元，所有焦元的集合称为核。设m1和m2分别是识别框架上Θ的基本可信任分配函数，有如下合成规则：

3 新技术实例分析

在实际故障诊断过程中，特征向量的选取是首要任务，这对最终诊断结果的有效性有着直接的影响。而在本文的研究中，主要是以电机转子的故障情况作为研究对象，那么我们就可以将故障诊断工作的重点转化到对转子振动频谱的检测上来。基于上述情况，在本文的研究中采用了振动信号频谱中每一个频段上的差异频谱峰值作为特征向量，并通过对其所代表的不平衡（y1）、不对中（y2）等6种故障类型进行识别模型建设，取频谱 中（0.01～0.39）f、（0.4～0.49）f、0.5f、（0.51～0.99）f、f、2f、奇数倍f、偶数倍f峰值作为此识别框架中的识别证据体。

完成上述工作之后，需要对所选择的3个传感器提供的信息进行处理，然后按照上文中介绍的蚁群神经网络来对故障情况进行分析，从而集合每一个传感器的可信任分配函数值，经过证据理论处理之后即可对故障类型进行有效的判断和界定了。其具体的归一化处理过程可以简单地用公式（6）加以表示：

式中，Ti表示第i个蚁群神经网络的输出；T′i代表了归一化后第i个网络的输出。

在按照上述流程完成归一化处理之后，将其结果作为“转子径向碰摩故障”的可信度进行分配，具体数据情况如表1所示。通过对该表的分析我们可以发现，具体的分配值为0.78、0.85、0.87。

表1 3个传感器可信度的分配情况

对上式进行整理，分别对传感器1、2的数据进行处理，k＝0.3×（0.12＋0.85＋0.01）＋0.18×（0.02＋0.85＋0.01）＋0.78×（0.02＋0.12＋0.01）＋0.01×（0.02＋0.12＋0.85）＝0.314 7，m（y1）＝0.03×0.02／（1－k）＝0.000 9，而其他影响能力相对较小的可信度计算过程省略，那么其具体的融合情况如表2所示。在这一过程中，转子径向碰摩故障的这一数值将会进一步提升到0.971 3，而相应地，对转子不对中故障的可信度降为0.031 6。同时，我们将传感器3所提供的数据和上文中的融合数据进行融合，使k＝0.156，其融合情况如表3所示。通过对表3进行简单分析后我们可以发现，该数值可信度提升到1.0的水平，从而就能够有效地分析出转子径向碰摩故障，而这一判定结果和实际情况是一致的。

为了验证本文所研究的诊断技术的有效性，我们假设传感器3出现故障，同时假设该传感器单独有效判断出碰摩事故的可能性非常小。我们以表4的数据作为该传感器的假定可信度分配情况，其融合情况如表4所示。

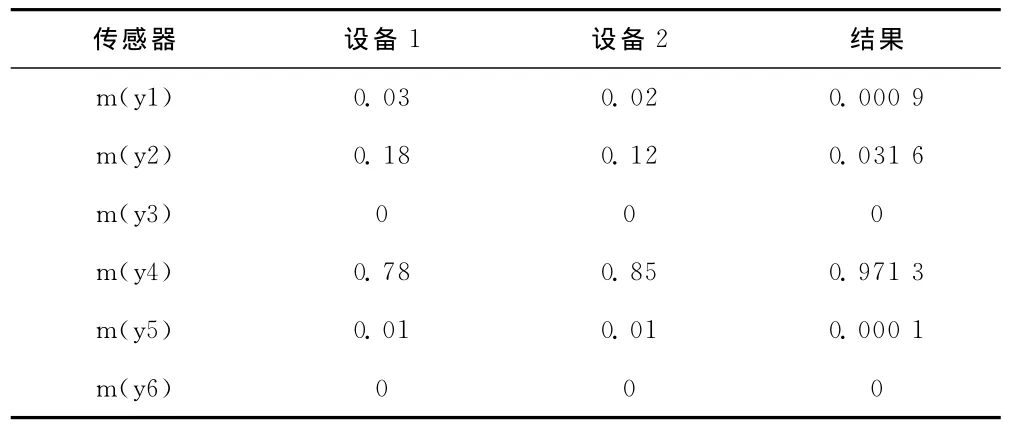
表2 传感器1和传感器2融合结果分析

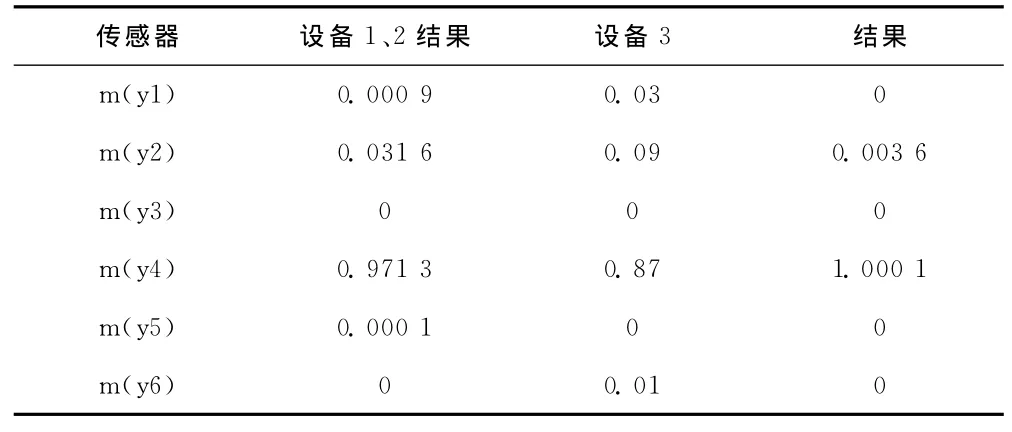
表3 传感器1、2和传感器3融合结果分析

表4 假设设备3故障时的融合结果分析

通过对表4进行初步分析我们可以发现，在本文所研究的多传感器环境下的故障诊断算法中，如果单一传感器出现故障，并不会对最终结果产生较大的影响，最终的诊断结果仍然具有较高的有效性。

4 结语

本文重点分析了基于证据理论的多传感器融合技术配合蚁群神经网络算法在电机故障诊断中的应用情况，有效地突破了传统单一传感器在电机故障诊断中应用的局限性，这对于提高诊断有效性和准确性具有非常重要的现实意义。实际上，多传感器信息融合过程中，本研究集中采用了实证分析的方式论证了其可行性，为其他故障诊断方法的研究提供了基础。

［1］王仲生，赵鹏.基于多源信息融合的发动机转子早期故障识别［J］.西北工业大学学报，2009（3）：326～329

［2］杨景明，孙晓娜，车海军.基于蚁群算法的神经网络冷连轧机轧制力预报［J］.钢铁，2009（3）：52～55

［3］李将军，叶仲泉，宫子风.改进蚁群算法及其仿真研究［J］.计算机应用，2008（12）：94～96