月面回转钻进采样非脆弱鲁棒控制
郑燕红,邓湘金,赵志晖,姚猛,邹昕
(北京空间飞行器总体设计部,北京100094)
月面回转钻进采样非脆弱鲁棒控制
郑燕红,邓湘金,赵志晖,姚猛,邹昕
(北京空间飞行器总体设计部,北京100094)
回转钻进采样技术是实现月面采样任务的重要手段。回转采样机构在月面复杂环境下会发生模型摄动,并受到外部扰动的影响,采样控制器的鲁棒性对顺利完成采样任务具有重要意义。本文针对回转采样机构,分析了采样过程中的模型摄动、外部扰动影响,建立了采样机构状态空间模型,利用线性矩阵不等式方法设计了状态反馈非脆弱鲁棒控制器,仿真结果表明:在有界模型摄动、有界随机系统扰动情况下,回转钻进采样控制系统内稳定,并对扰动具有抑制能力。
月面采样;回转钻进;非脆弱;鲁棒控制
0 引言
我国探月工程确定了“绕、落、回”三步走的发展思路[1-2],随着“嫦娥3号”探测器在月面成功实现软着陆与巡视勘察,从月球上自动采集样品并返回地球将是我国深空探测的重要目标之一。月球探测方面,6次Apollo载人登月任务、3次Luna无人采样返回任务,共获得了约382 kg月球样品,为人类研究月球起源与演化提供了宝贵的资料。回转钻进采样技术在样品获取过程中均扮演了重要角色。钻进采样过程中,回转机构在钻压力的辅助下,完成对土壤的切削、破碎、收集、排出等工作。
回转钻进采样过程中,采样控制器驱动回转采样机构完成样品破碎与获取,由于月面环境尤其是月壤特性具有一定的不确定性[3],实施过程中的采样性能与设计状态往往存在较大差异。文献[4]对苏联Luna任务采样机构形式、相关指标以及实施情况进行了介绍,其中Luna 16、Luna 20两次任务均发生了采样机构钻具卡滞现象,尤其是Luna 20在25 cm的钻进过程中由于卡滞导致过热,多次发生停转。Luna 24改进了采样机构设计,采样控制器也针对月壤密度可能的变化进行了输出功率适应性设计[5]。Apollo 15采用了手动月球表面钻获取次表层样品,当钻进深度大于0.9 m时,月球样品密实度显著增加,Apollo 16、17在Apollo 15任务后针对钻杆接头与岩芯提取器进行了改进[6],通过宇航员的多次调整完成了采样任务。从Luna、Apollo等任务实施过程来看,月面环境的复杂性对采样过程有重要影响,但目前研制的钻进采样机构[7]主要集中在提升机构本身的能力方面,而通过提升采样控制器对不确定对象的鲁棒性、对系统扰动的抑制能力,提高采样设备的适应性研究还较少。本文针对回转钻进采样机构,分析了月面钻进采样过程中的模型摄动、系统扰动,建立了控制系统数学模型,利用线性矩阵不等式方法设计了状态反馈非脆弱鲁棒控制器,并在模型摄动、外部扰动同时存在的情况下,对控制系统的稳定性、干扰抑制情况进行了仿真分析。
1 回转采样机构状态空间描述
月面采样过程中,回转采样机构通过电机组件驱动钻杆进行回转运动,钻杆外螺旋切削破碎月球风化层土壤,在向下的钻压力辅助下,中空的钻杆完成样品收集,并通过外螺旋将多余的细屑排至月球表面。设回转采样机构工作过程中,控制输入u∈Rr,状态量x∈Rn,调节输出z∈Rm,其状态空间描述为
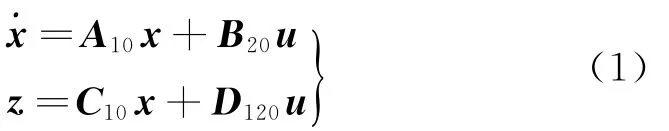
式中:A0,B20,C10,D120为相应维数的系数矩阵。
然而由于月面与地面温度环境存在较大差异,月昼温度往往高于地面环境温度,回转机构工作时,无法依靠大气对流散热,其温升特性将会发生一定的变化,电机的电阻、电感等内部参数会发生一定的漂移,从而导致模型具有参数不确定性,地面验证过程中具有良好性能设计的控制器在月面性能可能下降,甚至不能工作。月面环境引起的参数不确定性引入的摄动项为ExΔxFx,其中下标x表示对应的系数矩阵,||Δx||∞<1,具有不确定结构。
回转采样机构带动钻杆运动的主要负载为月壤,其负载特性受到月壤颗粒大小、粒径级配、相对密度等多个因素影响,而在不同采样点或同一采样点下不同采样深度均存在一定的差异,回转采样机构的负载特性将发生波动,并存在较大的不确定性。此外,回转采样机构包含多个轴承、齿轮进行传动,各部件的润滑性能在月昼真空高温环境下将发生一定的变化,回转采样机构内部阻力矩也会发生波动。将回转采样机构传动特性以及月壤负载特性引起的力矩波动,作为系统扰动量,记为ω∈Rl。因此,式 (1)回转采样机构名义模型,考虑摄动与扰动影响可描述为

式中:A=A0+EaΔaFa,B1=B10+Eb1Δb1Fb1,B2= B20+Eb2Δb2Fb2,C1=C10+Ec1Δc1Fc1,D11=D110+ Ed11Δd11Fd11,D12=D120+Ed12Δd12Fd12。其中:Ea、Fa、Eb2、Eb1、Fa∈Rn×n,Ec1、Ed11、Ed12∈Rm×m,Fb1∈Rn×l,Fb2∈Rn×r,Fc1∈Rm×n,Fd11∈Rm×l,Fd12∈Rm×r为加权阵,B10,D110为无摄动情况下的扰动系数矩阵。
2 非脆弱鲁棒控制器
回转采样机构多采用电机进行驱动,可选用转速、电流作为状态变量,并可通过相应的传感器进行测量,因此在控制器设计过程中可采用状态反馈设计。然而控制器的实现离不开物理器件,由环境变化、器件老化、测量元件精度不足等因素导致的控制器参数变化可能影响系统性能甚至稳定性,因此在控制器设计时,应保证控制器具有非脆弱性,采用无记忆状态反馈

式中:H=EKΔKFK,||ΔK||∞<1。将式(3)代人式(2)中,有如下闭环形式

本节的主要工作是寻找如式(3)所示的非脆弱状态反馈K0,使式(4)二次稳定,并对扰动具有抑制能力。
引理1 (Schur补引理)[8]:对于对称矩阵,其中L11∈Rr×r,则L<0等价于

引理2[9]:设L,M,N为适当维数的矩阵,且L为对称阵,对于矩阵F若满足FTF≤I,则

等价于存在一个正数κ,使

定理:对于给定的α>0,存在矩阵W、正定阵Q、单位阵I、正数β,满足如下不等式
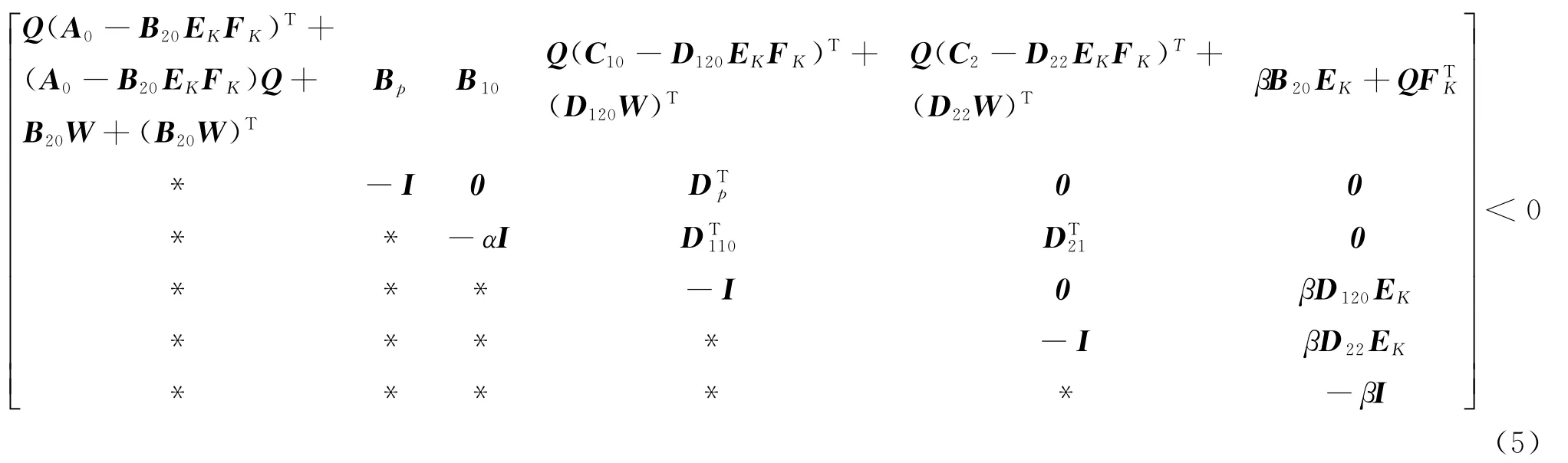
那么,式(2)所示系统采用状态反馈设计系统稳定,具有非脆弱性,且,状态反馈阵K0=WQ-1。
证明:由前面叙述知,式(2)所示系统引入状态反馈设计后,闭环形式如式(4)所示,其状态空间描述中系数矩阵A,B1,B2,C1,D11,D12存在摄动,将摄动项代人,引入中间变量p,q,整理可得


设V(x)=xTP0x,记Ac=A+B2K,C1c=C1+ D12K,C2c=C2+D22K,并构造如下不等式

整理可得

由引理1,式(8)可转化为


将式(9)中K=K0+EKΔKFK展开,即
式中:

由前面介绍的引理2,可知存在一个正数ε,使式(10)转化为


合并整理,并再次利用引理1升阶,可得

从上面的推导知,满足式(5)约束则式(7)成立,由式(7)两边对时间t从0到∞积分,并考虑||Δ| |∞<1,且系统为零初始状态V(0)=0,有



图1 恒值扰动、模型摄动下状态量及控制量变化曲线Fig.1 State and control variable curves with constant disturbance and model perturbation
3 仿真分析
设回转采样机构驱动电机参数名义值为ke= 0.15 V/rpm,kt=0.32 N·m/A,L=0.000 7 H,R= 0.7Ω,J=1.7×10-4kg·m2,以回转电机输出转速、绕组电流为状态变量x1,x2,工作过程中力矩波动为外部扰动ω,并以输出转速作为调节输出量z,则

考虑在月面工作过程中,回转电机各参数摄动为名义值的5%,由于此处选定的调节输出为回转电机直接输出的转速,其系数矩阵无摄动,考虑控制器状态反馈阵参数摄动在10%以内,因此,可确定名义模型各系数矩阵的摄动系数阵为

根据式(5),利用Matlab求解非脆弱状态反馈阵,可得

当恒值外部扰动ω为1 Nm时,考虑模型摄动系数矩阵不确定结构为Δa=delta I2×2,Δb1=Δb2=delta,其中delta分别为±0.3、±0.6、±0.9,可得模型摄动与扰动条件下,状态变量x1,x2以及控制量u变化情况如图1(a)、1(b)、1(c)所示。从图1中可见,存在摄动的系统受到恒值扰动时,状态量在很短的时间内达到稳定,控制量u,扰动输出指标z(等于x1)均有界,控制系统内稳定,从图1(a)仿真曲线的最终稳态值可见,闭环系统对恒值扰动信号具有干扰抑制能力。
4 结论
本文针对月面回转钻进采样机构,分析了月面钻进采样过程中的模型摄动、外部扰动影响,建立了采样机构的状态空间模型,考虑到控制器本身可能发生的参数摄动影响,进行了非脆弱状态反馈设计,利用线性矩阵不等式方法推导了非脆弱鲁棒控制器的存在条件,并针对特定的回转采样机构参数进行了仿真分析,结果表明在模型摄动、外部扰动同时存在的情况下,回转采样控制系统内稳定,并对外部干扰具有一定的抑制作用,为月面回转钻进采样控制器性能优化提供了途径。
[1]叶培建,彭兢.深空探测与我国深空探测展望[J].中国工程科学,2006,8(10):13-18.[Ye P J,Peng J.Deep space exploration and its prospect in China[J].Engineering Science,2006,8(10):13-18.]
[2]欧阳自远.我国月球探测的总体科学目标与发展战略[J].地球科学进展,2004,19(3):355-358.[Ouyang Z Y.Scientific objectives of Chinese lunar exploration project and development strategy[J].Advance in Earth Sciences,2004, 19(3):355-358.]
[3]杨帅,孙京,殷参,等.地外星体土壤取样机构技术[J].航天器工程,2011,20(4):138-144.[Yang S,Sun J,Yin S,et al. Soil sampling technology on extraterrestrial bodies[J]. Spacecraft Engineering,2011,20(4):138-144.]
[4]刘志全,庞彧,李新立.深空探测自动采样机构的特点及应用[J].航天器工程.2011,20(3):120-125.[Liu Z Q,Pang Y, Li X L.Characteristics and applications of automatic sampling mechanisms for deep space exploration[J]. Spacecraft Engineering,2011,20(3):120-125.]
[5]Apollo program summary report synopsis of the Apollo program activites and technology for lunar exploration[R].Houston: Lyndon B.Johnson Space Center,NASA-TM-X-68725,1975.
[6]Yoseph Bar-Cohen,Kris Zacny.Drilling in extreme environments-penetration and sampling on Earth and other planets[M].Weinheim:Wiley-VCH,2009:48-51.
[7]Grant H Heiken,David T Vaniman,Bevan M French.Lunar sourcebook-a user's guide to the moon[M].Cambridge: Cambridge University Press,1991:322-328.
[8]俞立.鲁棒控制—线性矩阵不等式处理方法[M].北京:清华大学出版社,2002:8-9.[Yu L.Robust control—linear matrix inequality approach[M].Beijing:Tsinghua University Press,2002:8-9.]
[9]贾英明.鲁棒H∞控制[M].北京:科学出版社,2007:198-199.[Jia Y M.Robust H∞control[M].Beijing:Science Press,2007:198-199.]
Non-Fragile Robust Control for Lunar Rotary-Drill Spamling Technology
ZHENG Yanhong,DENG Xiangjin,ZHAO Zhihui,YAO Meng,ZOU Xin
(Beijing Institute of Spacecrft System Engineering,Beijing 100094,China)
Rotatory drilling is a key technology to lunar sampling mission.Model perturbation of rotatory drilling mechanism exists in lunar complex environment.And system disturbance always influences the control system performance.Robust of controller plays an important role in sampling mission.Perturbation and disturbance was analyzed in the state space description.The state feedback non fragile robust controller was induced with linear matrix inequality method.Simulation results proved that the controller is inner stable with bounded model perturbation and has suppression ability to disturbance.
Lunar sampling;rotatory drilling;non fragile;robust control
:
:2095-7777(2014)04-0315-05
10.15982/j.issn.2095-7777.2014.04.012
郑燕红(1982—),男,主要研究方向为地外天体采样封装技术。
[责任编辑:宋宏]
2014-10-14
2014-10-30
E-mail:ZhengyhSince2014@hotmail.com

