脉冲星非实时平差的火星探测自主导航模型
魏二虎,杨洪洲,2,张帅,刘经南,易慧
(1.武汉大学测绘学院,武汉430079;2.卡尔加里大学测绘工程系,加拿大卡尔加里T2N 1N4; 3.武汉大学卫星导航定位技术研究中心,武汉430079;4.北京测绘科学研究院,北京100830)
脉冲星非实时平差的火星探测自主导航模型
魏二虎1,杨洪洲1,2,张帅1,刘经南3,易慧4
(1.武汉大学测绘学院,武汉430079;2.卡尔加里大学测绘工程系,加拿大卡尔加里T2N 1N4; 3.武汉大学卫星导航定位技术研究中心,武汉430079;4.北京测绘科学研究院,北京100830)
针对基于X射线脉冲星观测的火星探测器自主导航,研究了几种不同的实时自适应方法,包括:扩展卡尔曼滤波(EKF),自适应扩展卡尔曼滤波(AEKF)和鲁棒自适应扩展滤波(RAEKF)。首先根据脉冲星导航原理,模拟了观测值:脉冲到达时刻;接着,分别利用扩展卡尔曼滤波,自适应扩展卡尔曼滤波和鲁棒自适应扩展滤波方法估算出探测器的位置和速度;最后,上述几种滤波轨道与STK模拟的标称轨道较差,然后比较它们的滤波精度发现:AEKF和RAEKF的精度相对较高,AEKF的三个轴向滤波位置精度达到:X轴优于100 m、Y和Z轴优于30 m,优于VLBI技术的km量级,和Doppler技术的精度相当。
X射线脉冲星;自主导航;自适应扩展卡尔曼滤波;鲁棒扩展卡尔曼滤波
0 引言
火星探测是继月球探测之后又一个深空探测的热门领域,探测器的导航和定位决定着火星探测活动的成败与否。俄罗斯的“福布斯号”火星探测器的发射失败再一次说明了自主导航在火星探测活动中的重要性。应用于月球探测的导航技术如:VLBI和多普勒技术需要地面站的跟踪、观测和通信,它们不能满足火星探测的精度要求[1-2]。此外,火星探测器与地球的遥远距离也制约着这些技术的应用。因此,利用自主导航技术的火星探测器的发展可以弥补传统导航定位技术的缺陷,降低探测器对地面跟踪站的依赖,从而最大限度地确保火星探测活动的成功实施。基于X射线脉冲星的自主导航是一项新的极具潜力的自主导航技术,给深空探测器实现自主导航带来了希望。
本文正是基于这一背景,对基于X射线脉冲星的火星探测器自主导航技术进行了研究。首先,介绍了相关的坐标系统及其之间的转换关系;其次,选择了具有高观测精度的脉冲星用于自主导航实验;最后,结合火星探测器的动力学模型和脉冲星观测模型设计了一款自适应扩展卡尔曼滤波器,并开展了相关的数值实验和结果分析。
1 相关坐标系统
在基于X射线脉冲星的火星探测器自主导航中涉及的坐标系包括:太阳系质心坐标系(SSB),火星赤道惯性坐标系(SMCI)和火星中心惯性坐标系(SECI)。文献[3-4]对上述几种坐标系的定义做了相关介绍。这几种坐标系之间的转换关系可以用下面的公式表示

式中:RMCI2ECI是由SMCI到SECI的转换矩阵;RSB是探测器在SSB中的位置向量;RMCI是探测器在SMCI中的位置向量;RM是火星质心在SSB中的位置向量,可以从JPL的DE421星历表中查询得到;F、I和E是由SMCI向SECI转换的欧拉角,也可以由DE 421获得。
因为火星探测器动力学模型是在SMCI中描述的,而脉冲观测模型是在SECI中建立的。需要将脉冲星时间预报模型从太阳系质心转换到火星质心,转换精度达到0.1μs5。
2 自适应扩展卡尔曼滤波
2.1 轨道动力学模型
环火探测器的轨道动力学模型是非线性的,在惯性坐标系SMCI中可以由下述公式来描述。

式中:r=(x,y,z)是探测器的位置向量;μM代表火星引力常数;W代表状态噪声矩阵,是方差为Q的白噪声;ar表示模型摄动加速度。研究表明火星非球形摄动的J2项是主要的摄动因素[5],在轨道动力学模型中仅考虑J2项摄动因素,由此可得

因此探测器的状态向量可以定义为

式中:v是火星探测器的速度向量,火星探测器的动力学模型可以表述为

已知某一历元探测器的初始状态值,可以利用式(6)通过数值积分获得下一历元的状态值。
式(6)描述的是一个非线性系统,而传统的卡尔曼滤波主要针对线性系统问题。扩展卡尔曼滤波却可以应用于非线性系统的状态估计。
经过线性化后,环火探测器的系统扰动方程可表示为[6]

经离散化,式(7)可写作

式中:Φk|k-1是系统状态转移矩阵。
2.2 状态转移矩阵的计算
文章采用Markley方法计算状态转移矩阵。它的计算需要利用tk和tk-1的探测器状态值,μM、J2、Δt和火星半径等。该方法在很短的时间间隔Δt内,用泰勒级数展开近似计算状态转移矩阵。
根据Markley方法的原理,状态转移矩阵可以近似表示为式(9),其中:Φ(t0,t0)=I。

由于加速度对位置的偏导数矩阵G是状态值的函数,可以通过数值积分获得[78],因此,状态转移矩阵是可以通过积分计算的。如果仅考虑中心天体的J2项摄动加速度[9]影响,矩阵G可表示为
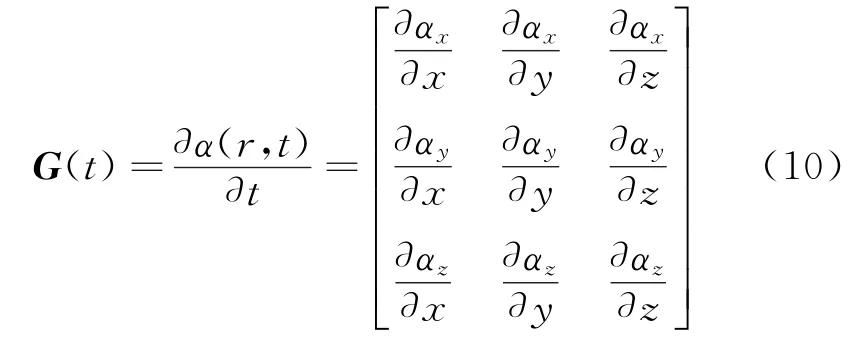
2.3 测量模型
用于卡尔曼滤波算法的测量模型可以表达为

式中:Z表示脉冲观测值;v为白噪声向量,代表随机测量误差,具有下列统计特性:

式中:δkj是克罗内克符号,当时其值为1,否则为0;v可以通过分析脉冲星TOA观测精度得到,R表示观测噪声的协方差矩阵。
Hk是观测方程矩阵,根据基于X射线脉冲星的环火探测器自主导航原理可知

式中:nT表示在SECI的脉冲星方向矢量,因为脉冲星与火星距离遥远,所以可以认为该方向矢量与在SSB相同。
3 数值实验
为了验证基于X射线脉冲星的自主导航技术的有效性,需要开展有效的数值实验,文章设计了几款扩展卡尔曼滤波器用于数值计算。
3.1 脉冲星测距精度
在利用脉冲星导航过程中,需要选择最合适的脉冲星。除了要考虑脉冲星的位置、基本属性等,还要顾及脉冲星测量精度。脉冲到达时刻的测量精度可以用下述公式描述[8]

式中:σr表示利用脉冲星测距精度;σTOA代表脉冲到达时刻TOA的测量精度;SNR是脉冲星脉冲星号的信噪比;BX表示X射线背景辐射流量;FX为X射线光子流量;A为探测器有效探测面积;T是观测时刻;pf为脉冲流量比;d为脉冲宽度比;W50%表示脉冲轮廓宽度的50%;c是真空中光速值。
根据上述性质,实验选取了7颗脉冲星列于表1中。它们的测距精度信息也列于表中[1011]。

表1 优选脉冲星的测距精度Table 1 Ranging accuracy with observation time
3.2 观测值仿真
仿真实验中,环火探测器的标称轨道是利用Satellite Tool Kit(STK)软件仿真得到的,历元间隔为500 s。仿真轨道的初始轨道参数[12]见表2。

表2 火星探测器初始轨道参数Table 2 Mars parameters For observations simulation
在观测值模拟过程中,需要顾及探测器上的原子钟误差和将时间相位模型由太阳系质心转移到火星质心而引起的转换误差。实验中,在观测值中分别加入了10-9s的原子钟误差和10-7s的模型转换误差[8]。此外,还在观测数据中随机加入了表1中的测距误差,使得模拟观测值更加趋近于真实情况。
3.3 滤波
数值实验应用三种数值处理方法,包括EKF、AEKF和RAEKF。其中,AEKF又有两种不同的自适应因子选取方法。两种自适应因子的选取依据下述公式
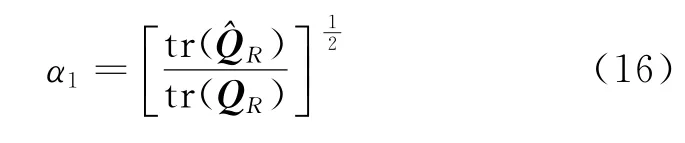


在RAEKF中,等价权的计算公式为式(19)和式(20),鲁棒最小方差估值的表达式为式(21)。

式中:k0和k1设置为1.5和2.5。滤波的初始参数设置如下:


3.4 结果和讨论
滤波计算中的一步预测值的计算是利用RKF7(8)数值积分器计算得到的。表3是具体的残差信息。从中可以看出,AEKF1、AEKF2和RAEKF滤波器的滤波结果明显优于EKF的结果;前三者的RMS值非常接近,其中又以AEKF1的精度最好,X、Y和Z三个轴向的位置精度分别达到了94.1 m、19.5 m和22.3 m。而X方向的精度较之Y和Z偏差可能与导航脉冲星的分布有关。
AEKF2要达到或接近AEKF1的精度有一个先决条件就是,它只能解决类似式(24)给出的观测方程,即必须具有多余观测值才能够高精度地解算状态参数值。因此AEKF1滤波器具有更好的实用性。
RAEKF与AEKF2类似,都要求多余观测。但是RAEKF的滤波精度略低于前两者,其原因可能是阈值设置而导致的自适应因子不恰当。所以需要继续改善自适应因子的选择方法,以便使得滤波精度进一步提高。

表3 EKF、AEKF1、AEKF2、RAEKF滤波结果比较Table 3 Comparison of the results from EKF、AEKF1、AEKF2、RAEKF m
从表3可以看出,3个轴向的速度误差基本上都分布在-0.1~1 m/s之间,其原因可能与式(21)中观测方程矩阵Hk的构造有关,Hk的最后三列的值均为0。在数值计算后,误差被吸收进位置参数中,从而确保了速度参数的高精度。在接下来的试验中,在初始状态值中分别加入了1 km的位置误差和0.5 m/s的速度误差。实验发现,上述4种滤波器具有类似的结果,其中尤以AEKF1的精度最好。图1和图2是AEKF1的滤波值与标称值的偏差示意图。

图1 AEKF1滤波值与标称状态的位置偏差Fig.1 Position bias between AEKF1 orbit and nominal orbit
可以看到,AEKF1在100历元后具有较高的收敛精度。因此,除了具有较高的精度外,AEKF1还能够抵抗初始误差的影响,获得精度优于1 km的位置滤波值和1 m/s的速度滤波值。
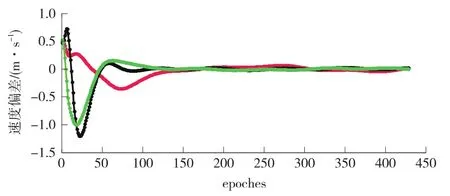
图2 AEKF1滤波值与标称状态的速度偏差Fig.2 Velocity bias between AEKF1 orbit and nominal orbit
4 结 论
上面的理论分析和数值仿真实验表明:基于X射线脉冲星的自主导航技术能够很好地胜任环火探测器的自主导航任务。实验数据显示,自主导航系统状态估计值在三个轴向X、Y和Z的位置精度分别可以达到:94.1 m、19.5 m和22.3 m。但是在实验中,若要获得上述精度的滤波值,需要观测7颗具有较高测距精度的脉冲星,这或许会限制系统的适用性。不过未来可以利用多频段天线或者多台独立的天线同时观测来解决这一问题。
在上面的实验中,AEKF1滤波器表现良好而且适用范围较广、受条件限制较小,因此该方法可以应用于火星探测器的自主导航中,从而弥补地面跟踪系统(包括VLBI、ΔDOR和ΔDOD)和测距技术的不足,尤其是当地面站跟踪不到探测器的时候。基于脉冲星的自主导航技术与地面跟踪系统的优势互补为未来的深空探测器导航指明了方向。
在本文的实验中,火星大气阻力、太阳光压和火星非球形引力的高阶项等摄动力因素并没有考虑进探测器的动力学模型中。若建立顾及上述诸多摄动因素的动力学模型,可以进一步提高探测器的导航定位精度。因此,如何完善火星探测器的轨道动力学模型需要进一步的研究。
[1]Cao J F,Huang Y,Hu X,et al.Mars express tracking and orbit determination trails with Chinese VLBI network[J]. Chinese Sci Bull,2010(55):3654-3660.
[2]李金玲,刘鹏,马茂莉,等.中国VLBI网火星快车卫星跟踪资料的定位归算[J].宇航学报,2010,31(7):1718-1723.[Li J L,Liu P,Ma M L,et al.Positioning reduction of the mars express tracking data by the Chinese VLBI network[J].J. Astronautics,2010,31(7):1718-1723.]
[3]Wei J,Xu S.Analysis on the influence of natural convection during melting of phase change materia[J].Chinese Space Sci.Tech,2009,29(2):65-70.
[4]Brukhart P D.MSL update to Mars coordinate frame definitions[EB/OL].[2014-07-29].http://www. coursehero.comfile2541877 HW4.2006-08-15:1-20.
[5]刘林,汤靖师.火星轨道器的运动变化特征[J].宇航学报, 2008,3(2):462-466.[Liu L,Tang J S.Orbit variation characteristics of the Mars'orbiters[J].J.Astronautics, 2008,3(2):462-466.]
[6]帅平,李明,陈绍龙,等.X射线脉冲星导航原理与方法[M].北京:中国宇航出版社,2009:466-470.[Shui P,Li M,Chen S L,et al.Principles and methods of X-ray pulsars navigation [M].Beijing:China Astronautic Publishing House,2009: 466-470.]
[7]Markley J.Approximate cartesian state transition matrix[J]. Journal of the Astronautical Science,1986,34(2):161-169.
[8]Chiaradia A P M,Kuga H K.Comparision between two methods to calculate the transition matrix of orbit motion[J]. Mathematical Problems in Engineering,2012,2012 (768973):1-13.
[9]Moraes R V,Silva A A,Kuga H K.Simple orbit determination using GPS based on a least-squares algorithm employing sequential given rotations[J].Mathematical Problems in Engineering,2007(49781):1-8.
[10]Sheikh S I.The use of variable celestial X-ray sources for spacecraft for navigation[D].Maryland:Department of Aerospace Enginerring,University of Maryland,2005.
[11]Kargaltsev O,et al.X-ray pulsars database[EB/OL]. 2012.http://www2.astro.psu.edu/users/green/ psrdatabase.
[12]Lemoine F G,Smith D E,Rowlands D D,et al.An improved solution of the gravity field of Mars from Mars global surveyer[J].J Geophys.Res,2001,106(E10): 23359-23376.
[13]Wei E,Jin S G,Zhang A,et al,Autonomous navigation of Mars probe using X-ray pulsars:modeling and results[J]. Adv.Space Res,2013,51(5):849-857.
[14]Wei E,Jin S G,Yang H,et al.Simulation and results on realtime positioning of Chang'E-3 rover with the same-beam VLBI observations[J].Planetary and Space Science,2013,84:20-27.
[15]Yang Y,He H,Xu G.A new adaptively robust filtering for kinematic geodetic positioning[J].Journal of Geodesy,2001, 75(2):109-116.
通信地址:湖北省武汉市珞喻路129号武汉大学测绘学院空间定位与导航工程研究所(430079)
电话:(027)68758505
E-mail:ehwei@sgg.whu.edu.cn
[责任编辑:高莎]
Modeling on Autonomous Navigation of Mars Probe with Pulsars and Nonreal-Time Adjustment Methods
WEI Erhu1,YANG Hongzhou1,2,ZHANG Shuai1,LIU Jingnan3,YI Hui4
(1.School of Geodesy and Geomatics,Wuhan University,Wuhan 430079,China;2.Department of Geomatics Engineering, University of Calgary,Calgary T2N 1N4,Canada;3.GNSS Center,Wuhan University,Wuhan 430079,China; 4.Chinese Academy of Surveying and Mapping,Beijing 100830,China)
To investigate the autonomous navigation of probe orbiting the Mars orbit X-ray pulsars,different real-time adjustment methods are applied in this paper,including the extended Kalman filter(EKF),adaptive extended Kalman filter(AEKF)and robust adaptive extended Kalman filter(RAEKF).Firstly,the observation data,i.e.,time of arrival,is simulated according to the principles of pulsars navigation.Secondly,extended Kalman filter(EKF),adaptive extended Kalman filter(AEKF)and robust adaptive extended Kalman filter (RAEKF)are used to get the position and velocity of the probe.Thirdly,the adjustment results are compared with the orbit generated by STK,the results show AEKF and RAEKF performs better than EKF,the result of AEKF is better than the km level of VLBI and can reach the precision level of triple pass Doppler,leveling at 94.1 m in X-axis,19.5 m in Y-axis and 22.3 m in Z-axis.
X-ray pulsars;autonomous navigation;adaptive extended Kalman filter(AEKF);robust adaptive extended Kalman filter(RAEKF)
P1
:A
:2095-7777(2014)04-0298-05
10.15982/j.issn.2095-7777.2014.04.009
魏二虎(1961—),男,教授,博士生导师,主要研究方向为空间大地测量。
2014-07-29
2014-08-09
国家自然科学基金资助项目(41374012)

