改进的简单竞争指标在单木生长模型中的应用1)

覃阳平 张怀清 陈永富 蒋 娴 李永亮

(中国林业科学研究院资源信息研究所，北京，100091)

责任编辑:戴芳天。

单木的生长除了受林木种源、立地条件等因素影响外，更主要取决于单木个体在林分中的竞争能力。因此，如何采用适宜的竞争指标，科学、客观地评价林分中单木的竞争能力，是建立单木生长模型的基础，竞争指标的优劣直接影响单木生长模型的使用效果。大多数文献［1-6］中描述的竞争指标可以分为两类:与距离无关的单木竞争指标和与距离有关的单木竞争指标。根据关玉秀［7］等人的研究，竞争指标优劣的衡量标准如下:①竞争指标的构造具有一定的生理和生态学依据;②对竞争状态的变化反应灵敏，并具有适时可测性或可估性;③能准确地说明生长的变差;④构成因子容易测量;⑤竞争指标的计算尽量简单。

Hegyi简单竞争指标是与距离有关的竞争指标中较为简单的一种，其直接使用对象木与竞争木之间的距离及竞争木与对象木的直径之比来反映单木所承受的竞争压力。其特点:一是林木间距离及林木胸径都能精确实测;二是胸径比可以反映冠幅比;三是引用林木个体间的距离可以反映林木个体对空间的相对占有程度［8］。简单竞争指标基本上能满足上述竞争指标优劣的衡量标准，而且在计算上比较简单，表现形式也比较直观，因此在与距离有关的单木生长模型中的应用较多［8-10］。现有的简单竞争指标模型中模型参数(对象木直径、竞争木直径以及两者之间距离)的指数都为定值1，在本研究中从数学形式上对其进行扩展，扩展后的结果如公式(2)所示，探讨对象木直径、竞争木直径以及两者之间距离的指数为变量时，单木直径生长模型的拟合效果是否会更好。

笔者以湖南省攸县黄丰桥国有林场杉木中龄林为研究对象，改进简单竞争指标，建立以单木直径、竞争和立地条件为自变量，单木连年直径生长量为因变量的估算模型，实现单木直径生长量的预测，目的为研究杉木人工林生长模拟、经营管理以及更新森林资源调查数据库提供支持，同时也是为单木的反演、再现和预测奠定良好的基础，以便更好更全面地实现森林可视化。

1 研究区概况

研究地区为黄丰桥国有林场，位于湖南省株洲市攸县东西部，地理坐标为东经130°04'～113°43'，北纬27°06'～27°04'，东西长约60 km，南北宽约40 km。林场地貌以中低山为主，境内最高海拔1 270 m，最低海拔115 m，坡度一般在20°～25°。林场地处中亚热带季风湿润气候区，年平均气温17．8℃;极端最低温度-11．9℃，极端最高温度40℃;年≥l0℃积温5 609．9℃;平均无霜期为292 d;平均日照时间为1 612 h，年平均降水量1 410．8 mm，年内降水量春季占40%，夏季占32%，秋季占28%，属于林木生长旺季的4—9月份降水量占全年降水量的65%。林场的森林覆盖率为86．24%，主要造林树种为杉木(Cunninghamia lanceolata)、马尾松(Pinus massoniana Lamb)、楠竹(Phyllostachys pubescens)等。

2 材料与方法

2．1 数据来源及研究对象

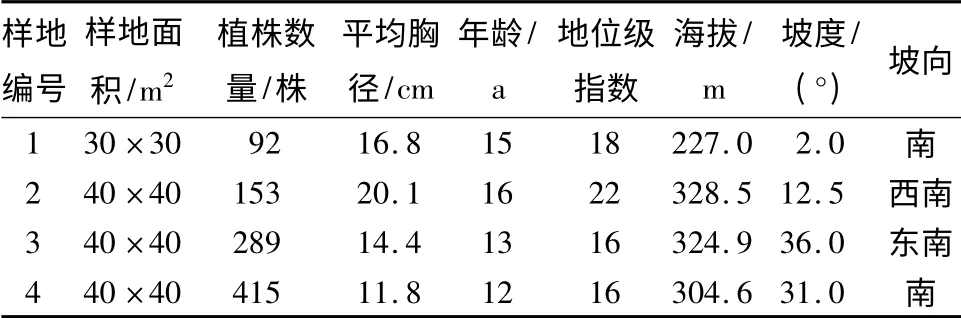
表1 样地基本信息

2．2 研究方法

2．2．1 简单竞争指标

Hegyi［2］直接使用对象木与竞争木之间的距离及竞争木与对象木的直径之比构造了简单竞争指标，其表达式如下:

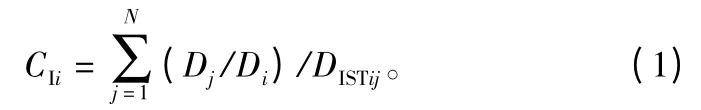
式中:CIi是对象木i的简单竞争指标;Di是对象木的直径;Dj是对象木周围第j株竞争木的直径(j=1，2，3，…，N);DISTij表示对象木i与竞争木j之间的距离。用单木定位固定样地资料计算简单竞争指数，有两个问题需要事先解决，一是对象木和竞争木范围的确定;二是竞争木数量的确定。本研究采用第4邻体距离判定法［12］来处理样地边界木;根据以前的研究［8，10，13-14］，人工林对象木周围竞争木的株数可以为为4、6、8株，同时综合考虑惠刚盈提出的最佳空间结构单元［15］，在本研究中选择4株来计算简单竞争指数。4个样地共有单木939棵，根据边界木的处理方法最终确定4个样地中有213棵边界木，在模型拟合时不考虑这些边界木，参与拟合的单木有736棵。

改进后的简单竞争指标如下所示:

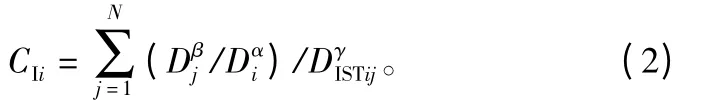
式中:CIi是对象木i的简单竞争指标;Di是对象木的直径;Dj是对象木周围第j株竞争木的直径(j=1，2，3，…，N);DISTij表示对象木i与竞争木j之间的距离;α、β、γ为待求的参数。

2．2．2 单木生长模型

根据以往的研究［16-20］，单木生长量可以看作是单木胸径、竞争因子和立地条件的函数，因此，确定单木连年直径生长量模型的基本形式如下:

6.吃黑 黑是指黑色食品。营养学家早就指出，天然食品中营养价值的高低不仅与食品的种类有关，还与自然色泽有关，其中黑色食品中营养价值最好。属于黑色食品的有黑米、黑芝麻、黑大豆、黑麦、黑木耳、乌鸡、甲鱼等，它们不仅口感好营养丰富，而且有较好的滋补食疗功能，并能提高免疫力，有抗癌防癌功效。

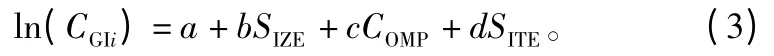
式中:DGIi是连年平方直径生长量(带皮);a是截距;b是单木胸径的向量系数;SIZE是单木胸径的函数;c是竞争因子的向量系数;COMP是竞争因子的函数;d是立地因子的向量系数;SITE是立地因子的函数。

对于林分中的单木胸径，采用林木的期初胸径(D)来表示:

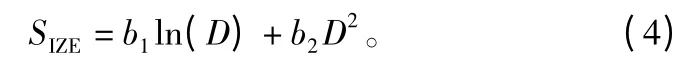
在本研究中，建立的是与距离有关的单木胸径生长量模型，因此用与距离有关的竞争指标来表示竞争因子的函数:

立地条件也是影响林木生长的重要因素。在外业调查中，与立地条件有关的地形因子是海拔、坡度、坡向等。参考前人［16］的研究工作，建立的立地条件的函数为:

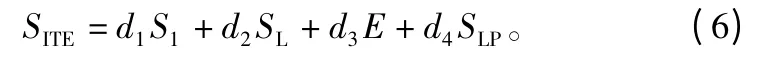
式中:di为待定参数(i=1～4);SI为地位级指数;E为海拔;SL为坡率值，即坡度的正切值;SLP为坡向，正北方为0°，正西方为90°，正南方为180°，以此类推。

将(4)、(5)、(6)式代入(3)式中，整理得到单木连年直径生长量与林木单木胸径、竞争指标和立地条件的基本模型为:

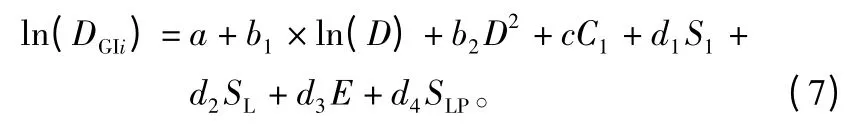
2．2．3 参数估计方法和模型拟合效果评价

对于改进前的简单竞争指标，即公式(1)参与拟合的单木生长模型(7)，式中的变量D、D2、SI、SL、E、SLP都是实测数据，CI也可以由实测数据计算得出，此时采用多元线性回归进行模型的拟合，最小二乘法求出参数的估计值;对于改进后的简单竞争指标，即公式(2)参与拟合的单木生长模型(7)，式中的变量D、D2、SI、SL、E、SLP都是实测数据，但由于CI的计算公式中多了3个参数α、β、γ，CI的值不能直接由实测数据计算得出，模拟的拟合也不能用多元线性回归;在本研究中采用非线性回归的方法进行模型的拟合，最小二乘法求出参数的估计值。构建模型时随机选择80%(590棵)的数据作为建模数据，20%(146棵)的数据作为检验数据。数据分析及建模均使用EXCEL2007和SPSSV20软件。

在多元线性回归中，随着模型中自变量数量的增加，决定系数R2将不断增大，但是这不能说明模型的拟合效果就是最好的，因为有些自变量对模型预测或者因变量解释根本起不到什么作用，这不符合回归模型中自变量数量尽可能少的原则。本研究采用表2所示的3种方法来评价模型拟合的优度。

表2 模型拟合效果评价方法

同时，如果自变量中有两个或多个解释变量出现了较强的相关性，就称模型中存在多重共线性。多重共线性虽然不违背最小二乘法的4个基本假设，但会使最小二乘回归估计的结果变得很坏［21］。在本研究中采用方差膨胀因子(VIF)来判断自变量间的多重共线性，VIF越大，共线性越强，当VIF≥10时，就说明自变量间有严重的多重共线性，且这种多重共线性可能会过度地影响最小二乘估计值。

3 结果与分析

3．1 模型的拟合和分析

对于改进前的模型采用逐步回归的方法对(7)式中各个变量进行筛选，此时用到的简单竞争指标公式为(1)，得到与距离有关的直径生长模型的拟合结果如表3所示。可以看出，在林木单木胸径平方(D2)、竞争因子(CI)成为模型的入选变量时，模型的拟合优度得到大幅度提升;同时立地因子(SL、SLP、E)进入模型后，模型的决定系数R2从0．481提升到0．710，模型的拟合优度得到了大幅度的提升。根据多元回归模型的选择标准:校正决定系数Rc最大，Cp统计量当尽可能地小，且应尽可能地与p值(模型中自变量数量)接近，AIC值越小等标准，确定最终的模型为模型5。在最终的模型中，立地条件(SL、SLP、E)对模型有较大的影响。虽然立地条件(SL、SLP、E)不是影响杉木生长的直接因子，但其能综合地反映影响杉木生长的各种直接因子，如海拔高度能反映垂直气候带的差别，不同的坡度、坡向因子能反映阳光辐射强度，小气候中的气温、湿度、植被覆盖的优劣和土壤湿度等，这些都对杉木生长有较大的影响。

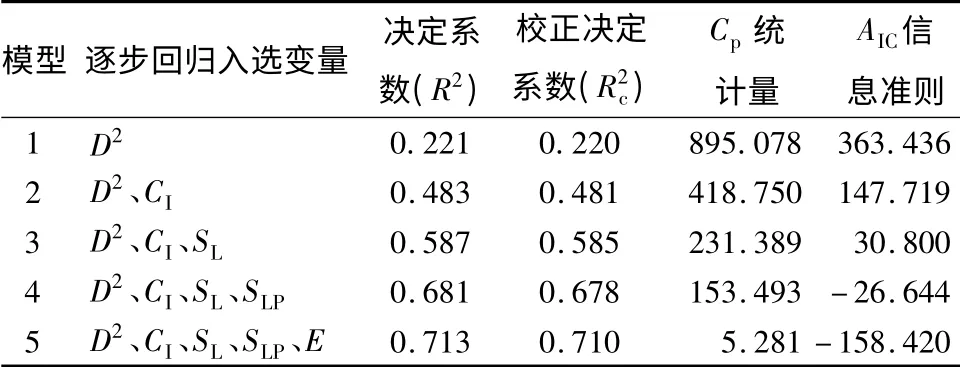
表3 直径生长模型拟合结果

通过对各个入选参数进行t检验，发现所有入选参数都是显著的。同时利用方差膨胀因子(VIF)判断变量的共线性，得出VIF的值远小于10，因此变量之间的共线性很弱，结果见表4，最终确定直径生长模型为:

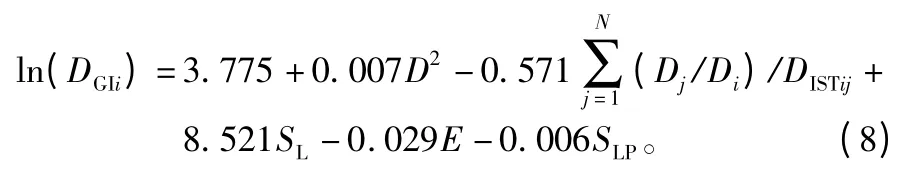
非线性回归的拟合结果见表5，可以看出改进后的简单竞争指标参与拟合的直径生长量模型的校正决定系数R2为0．763，显著高于多元线性回归的的结果(R2为0．710)，同时模型Cp统计量值为5．992，更接近于p值(模型中自变量数量为6个)，AIC的值为-216．719，显著低于多元线性回归的的结果(AIC为-158．420)。综合上述，改进后模型的拟合优度得到了大幅提升，说明简单竞争指标模型参数的指数为变量时，单木连年直径生长模型的拟合效果会更好。最终确定的单木连年直径生长量模型为:

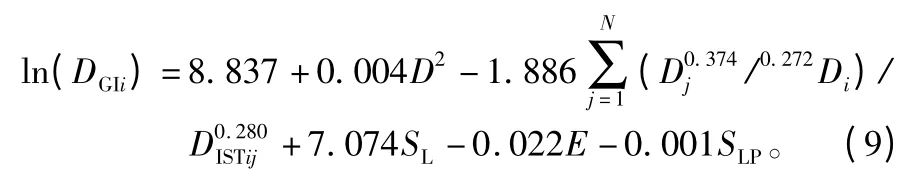
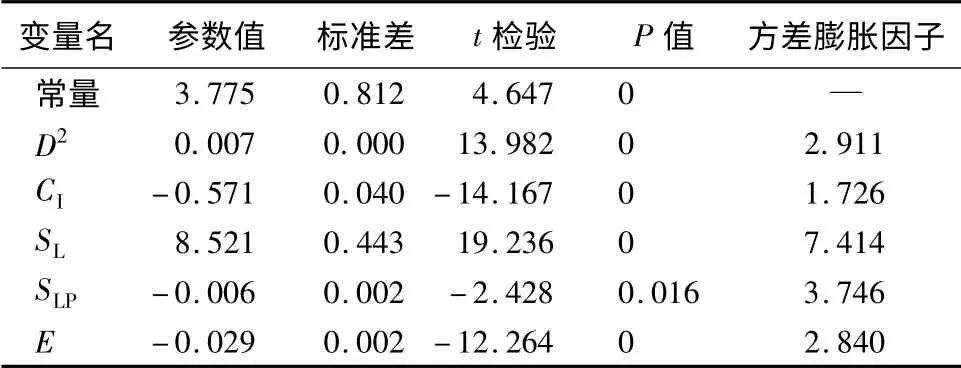
表4 直径生长模型统计量

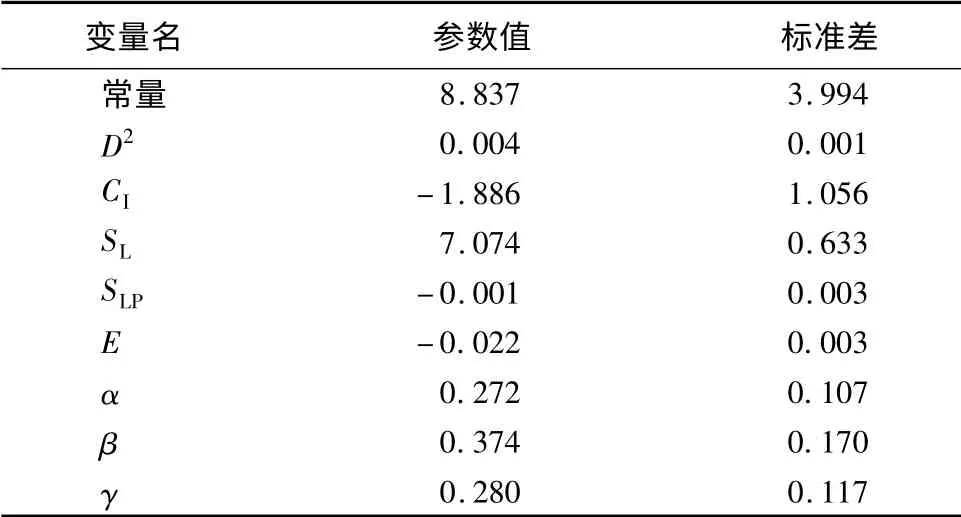
表5 非线性回归的直径生长模型统计量

3．2 模型的检验

使用公式(9)计算得到直径生长的预测值，然后与20%的实际值进行配对样本t检验，检验结果见表6。可以看出，冠幅预测值比实际值稍小，同时P值(0．071)大于0．05，这表明直径生长的预测值与实测值之间无显著差异。图1为模型预测值残差分布图，可以看出残差随机分布在0水平轴两端，残差分布范围大致在±0．5之间。这可以证明所建直径生长模型模型拟合效果较好，能够预测杉木直径的生长。

表6 直径生长模型结果t检验

图1 直径生长模型残差和预测值

4 结论与讨论

建立与距离有关的单木生长模型时，应考虑林木单木胸径、竞争因子和立地因子的综合影响。在林木单木胸径因子平方(D2)、竞争因子(CI)成为模型的入选变量时，模型的拟合优度得到大幅度提升;同时立地因子(SL、SLP、E)进入模型后，模型的决定系数R2从0．481提升到0．710，模型的拟合优度得到了大幅度的提升。虽然立地条件(SL、SLP、E)不是影响杉木生长的直接因子，但其能综合地反映影响杉木生长的各种直接因子，如海拔高度能反映垂直气候带的差别，不同的坡度、坡向因子能反映阳光辐射强度，小气候中的气温、湿度、植被覆盖的优劣和土壤湿度等，这些都对杉木有生长有较大的影响。

改进后的简单竞争指标参与拟合的直径生长模型的决定系数为0．763，显著高于未改进时的拟合结果(决定系数为0．710)，这说明在建立与距离有关的单木生长模型时，简单竞争指标模型参数的指数为变量时，单木连年直径生长模型的拟合效果会更好。

本研究建立的单木连年直径生长模型仅以杉木中龄林为研究对象，为了全面地预测杉木林分的生长，需要收集更多的样地数据(幼龄林、成熟林、过熟林等)建立模型。

该模型经过t检验、残差分析后均表明预测性能较好，因此该模型均可为研究杉木人工林生长、经营管理以及更新森林资源调查数据库提供支持，同时为杉木人工林更精确的可视化奠定了基础。

［1］Bella I E．A new competition model for individual trees［J］．Forest Science，1971，17:364-372．

［2］Hegyi F．A simulation model for managing jack-pine stands:In Growth models for tree and stand simulation［M］．Sweden:Royal College of Forestry，1974:74-90．

［3］Moore J A，Budelsky C A，Schlesinger R C．A new index representing individual tree competitive status［J］．Canadian Journal of Forest Research，1973，3:495-505．

［4］ToméM，Burkhart H E．Distance-dependent competition measures for predicting growth of individual trees［J］．Forest Science，1989，35:816-831．

［5］Holmes M J，Reed D D．Competition indices for mixed species northern hardwoods［J］．Forest Science，1991，37:1338-1349．

［6］Biging G S，Dobbertin M．A comparison of distance-dependent competition measures for height and basal area growth of individual conifer trees［J］．Forest Science，1992，38:695-720．

［7］关玉秀，张守攻．竞争指标的分类及评价［J］．北京林业大学学报，1992，14(4):1-8．

［8］黄家荣，万兆浜．马尾松人工林与距离有关的单木模型研究［J］．山地农业生物学报，2000，19(1):10-15．

［9］江希钿．用主成分分析构造竞争指标并建立单木生长模型［J］．福建林学院学报，1993，13(2):129-133．

［10］邵国凡．红松人工林单木生长模型的研究［J］．东北林业大学学报，1985，13(3):38-46．

［11］盛炜彤，童书振，段爱国．杉木丰产栽培实用技术［M］．北京:中国林业出版社，2011．

［12］周红敏，惠刚盈．林分空间结构分析中样地边界木的处理方法［J］．林业科学，2009，45(2):1-5．

［13］袁小梅，王久丽．单木生长模型和林分模拟系统的研究及应用(Ⅱ)［J］．北京林业大学学报，1992，14(1):89-95．

［14］邱学清，江希铀，黄健儿．杉木人工林竞争指数及单木生长模型的研究［J］．福建林学院学报，1992，12(3):309-316．

［15］惠刚盈．森林空间结构量化分析方法［M］．北京:中国科学技术出版社，2003:14-16．

［16］Monserud R A，Sterba H．Modelling individual tree mortality for Austrian forest species［J］．Forest Ecology and Management，1999，113:109-123．

［17］杜纪山．用二类调查样地建立落叶松单木直径生长模型［J］．林业科学研究，1999，12(2):160-164．

［18］卢军．长白山地区天然混交林单木生长模型的研究［D］．哈尔滨:东北林业大学，2005．

［19］Sönmezl T，Ercanli I．A distance-independent basal area growth model for oriental spruce(Picea orientalis(l．)Link)growing in mixture with oriental beech(Fagus orientalis Lipsky)in the Artvin region，North-East Turkey［J］．African Journal of Agricultural Research，2009，4(8):740-751．

［20］马武．蒙古栎林单木生长模型系研究［D］．北京:中国林业科学研究院，2012．

［21］吴明山．回归模型的估计方法及在林业中应用研究［D］．昆明:西南林业大学，2008．