威布尔模型的典型曲线及应用

陈元千，李 剑

（中国石油勘探开发研究院，北京100083）

威布尔模型的典型曲线及应用

陈元千，李 剑

（中国石油勘探开发研究院，北京100083）

威布尔模型是一个重要的预测模型，可以用于预测油田的产量和可采储量。该模型具有3个待定常数，属于非线性模型，在以往利用线性迭代试差法或非线性迭代试差法求解时，这2种方法比较繁琐且存在一定的不确定性。基于威布尔模型的基本方程，推导建立了模型的无因次关系式，研制了可用于人工拟合或计算机自动拟合的典型曲线，该典型曲线只有1个待定模型常数。根据拟合求解的模型常数可以对油田的产量、累积产量和可采储量进行预测。通过实例应用表明，研究内容和方法均正确有效。

威布尔模型典型曲线可采储量产量罗马什金油田

在概率统计学中，威布尔分布是一个著名的分布，它于1939年由威布尔正式提出，后于1995年由陈元千等经推导变换建立了威布尔模型［1］。预测模型按其建立的基础和描述的现象可划分为单峰周期模型和累积增长模型，其中威布尔模型［1］、翁氏模型［2］、瑞利模型［3］、陈-郝模型［4］和对数正态分布模型［5］属第1类模型；HCZ模型［6］和哈伯特模型［7］属第2类模型。由于威布尔模型具有较好的实用性，并具有2类模型的表达式，因此笔者对其进行无因次化研究，建立了无因次的威布尔模型，得到了可供人工拟合或计算机自动拟合求解的典型曲线。

1 威布尔模型及典型曲线

1.1 威布尔模型的主要关系式

威布尔模型的主要关系式［1］包括

1.2 无因次的威布尔模型和典型曲线

威布尔模型的无因次年产量、无因次累积产量和无因次时间可分别表示为

式中：QD为无因次年产量；NpD为无因次累积产量；tD为无因次时间。

利用式（7）—式（9），可由式（1）和式（2）分别得到威布尔模型年产量和累积产量的无因次关系式为

给定不同的tD值，由式（10）和式（11）可以分别求得相应的QD和NpD，由这些数据可以绘制无因次典型曲线图版（图1，图2）。

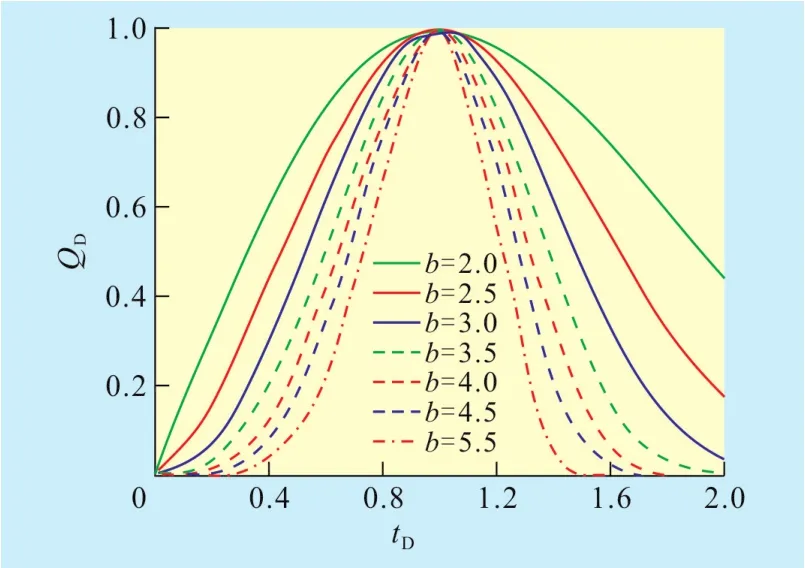
图1 威布尔模型QD与tD的典型曲线

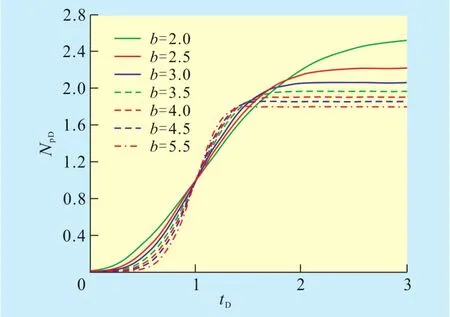
图2 威布尔模型NpD与tD的典型曲线

1.3 典型曲线拟合确定b值

根据式（7）—式（9），对油田的实际年产量、累积产量和开发数据进行无因次化处理，可得到油田的QD，NpD和tD的相应数值。利用QD，NpD和tD的相应数据，可以通过人工与典型曲线（图1和图2）相拟合，或通过计算机与典型曲线自动拟合，求得最佳拟合的b值。

1.4 预测油田的Q，Np和NR

在已知Qmax，tpeak和Npeak的数值，并已确定b值的条件下，年产量、累积产量和可采储量的预测公式分别为

2 应用实例

俄罗斯的罗马什金油田1953—1982年生产的油气当量数据列于表1［8］。油田生产的特征数据包括：Qmax=9 516×104m3/d，Npeak=112 076×104m3，tpeak=20 a，由式（7）、式（8）和式（9）计算的QD，NpD和tD见表1。

利用表1中QD与tD的相应数据，由计算机与典型曲线的自动拟合，求得模型常数b=2.5（图3）；再利用表1中NpD与tD的相应数据，由计算机与典型曲线的自动拟合，求得模型常数b=2.3（图4）。由式（12）和式（13）预测的Q和Np的数值（表1，图5）可以看出，预测值与实际值基本一致。将Npeak=112 076×104m3和b=2.5代入式（14）得油田的可采储量为24.8×108m3。

图3 罗马什金油田年产量拟合结果

图4 罗马什金油田累积产量拟合结果

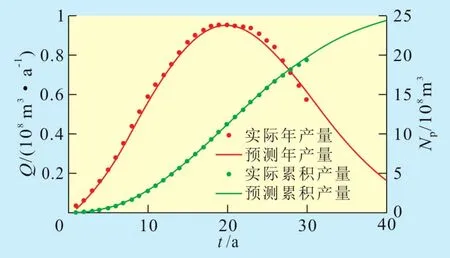
图5 罗马什金油田预测与实际产量对比

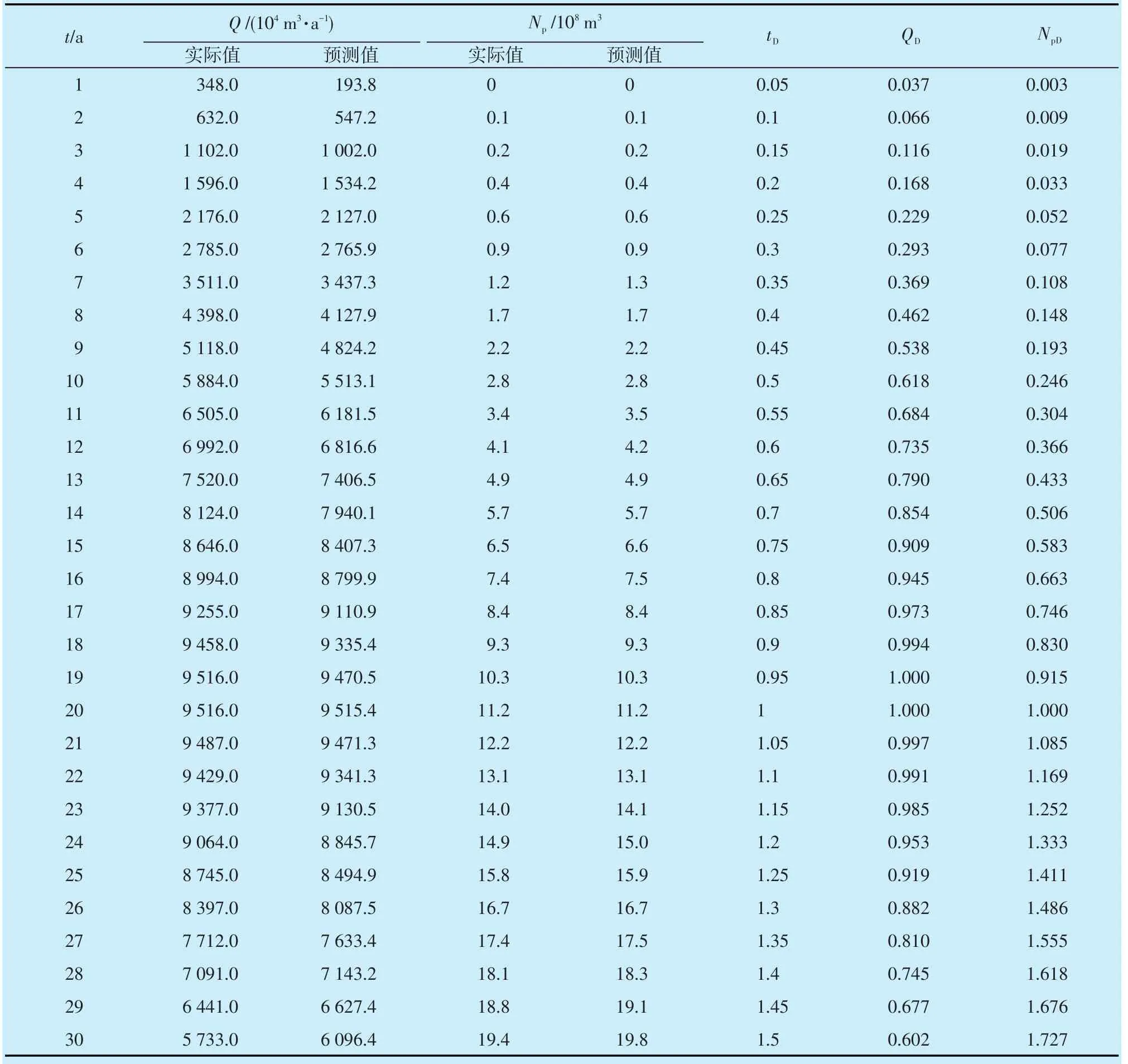
表1 罗马什金油田开发数据

3 结论

笔者提出的威布尔典型曲线及其拟合求解预测方法，不但可以用于预测油气田的产量、累积产量和可采储量，而且可以用于预测因开发调整方案和EOR项目的实施而增加的可采储量。同时，也可用于油气区，乃至中国的资源量、储量和产量的预测。实例的预测结果与实际数据基本一致。

威布尔模型是一个带有a，b和c共3个待定常数的非线性模型，对于这类模型，在文献［1］和文献［4］中，分别提出的线性迭代试差法和非线性迭代试差法在求解时均较为繁琐。而笔者提出的典型曲线方程只有1个模型常数b，且可以通过油田的无因次化数据与典型曲线拟合准确地得到，而直接用于产量、累积产量和可采储量的预测，而且油气田的储量愈小，则b值越大。

当油气田的开发出现多峰产量时，笔者提供的典型曲线法也可用于由文献［4，9］建立的多峰预测模型。

［1］ 陈元千，胡建国.预测油气田产量和可采储量的Weibull模型［J］.新疆石油地质，1995，16（3）：250-255.

［2］ 陈元千.对翁氏模型的推导及应用［J］.天然气工业，1996，16 （2）：22-26.

［3］ 陈元千.瑞利模型的完善推导及应用［J］.油气地质与采收率，2004，11（4）：297-299.

［4］ 陈元千，郝明强.多峰预测模型的建立与应用［J］.新疆石油地质，2013，34（3）：54-57.

［5］ 陈元千.油气藏工程实用方法［M］.北京：石油工业出版社，1999：46-55.

［6］ 胡建国，陈元千，张盛宗.预测油气田产量和可采储量的新模型［J］.石油学报，1995，16（1）：79-86.

［7］ 陈元千，胡建国，张栋杰.Logistic（罗辑斯谛）模型的推导与应用［J］.新疆石油地质，1996，17（2）：150-155.

［8］ 陈元千，邹存友.产量递减阶段储采比的变换规律［J］.新疆石油地质，2010，31（1）：66-68.

［9］ 陈元千，郝明强.HCZ模型在多峰预测中的应用［J］.石油学报，2013，34（4）：747-752.

编辑经雅丽

TE313.8

A

1009-9603（2014）01-0033-03

2013-11-22。

陈元千，男，教授级高级工程师，从事油气藏工程、油气田开发和油气储量评价等方面的科研、教学和评价工作。联系电话：（010）62398212，E-mail：lijianlijian@petrochina.com.cn。