曲率属性分析及其在地震资料解释中的应用

（中国石油大学（北京）， 北京 昌平 102249）

曲率属性分析及其在地震资料解释中的应用

李 澈，季天愚, 李雨澈

（中国石油大学（北京）， 北京 昌平 102249）

曲率属性分析是一项新兴的地震资料解释技术，近年来在西方国家得到了较为迅速的发展。该技术在识别地下微小断层、裂缝、孔洞发育带方面表现出良好的特性。从曲率属性的概念出发，论述了曲率属性分析的基本原理、分类，将曲率属性分析与其他属性分析方法进行了对比，最后通过实际例子展示了曲率属性分析技术在地震资料解释中的应用效果。

曲率属性；地震资料解释；分类；对比

随着石油勘探与开发的不断深入，寻找新的勘探目标难度越来越大，需要引入先进的地球物理技术来解决复杂的地质问题，如复杂断块、微小断层的精细解释、碳酸盐岩储层裂缝预测等。曲率属性分析技术近年来在西方国家得到了日益广泛的应用，作为一项新的技术，其主要用于识别断层和裂缝，可以揭示与断层、线性特征及局部构造等方面有关的大量信息。

1 曲率属性的概念和地质意义

1.1 曲率属性的概念

曲率是曲线的一种二维特征，如图1所示它描述了曲线上某点的弯曲程度。过一条曲线上某点P存在着一个圆，它满足在与曲线相切的圆中与曲线接触面积最大，该圆称为密切圆[1]。P点的曲率K等于过该点的密切圆半径R的倒数：该表达式还可以表述为导数形式：

曲率的二维概念可推广到三维，x如图2所示：空间上某点，在任意方向上可得到一个曲率值，其中正交于层面的平面所定义的曲率称为法曲率[2]。

图1 二维曲率的数学意义Fig.1 Mathmatic meaning of 2D curvature

1.2 曲率属性的地质意义

如图3所示，在将曲率属性应用于构造解释时，水平或斜平地层的曲率被定义为零，背斜的曲率定义为正值，向斜定义为负值。二者的绝对值随着弯曲程度的增加而相应增加。曲率属性量化了曲线偏移直线的角度，有助于淡化局部的倾角作用，强调与沉积特征或小尺度断层相关的线性特征[3]。

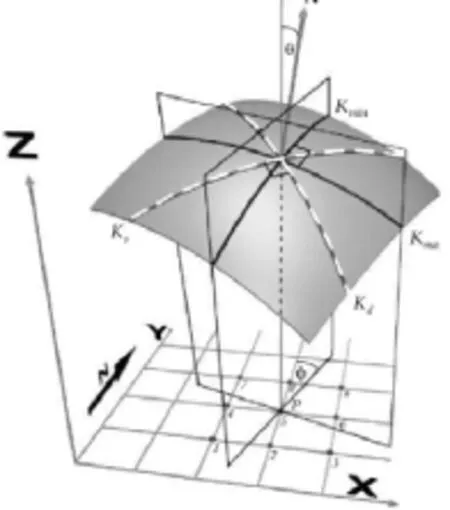
图2 三维空间中的曲率Fig.2 Curvature in 3D space

将这些对构造变形和弯曲程度的定量描述与已有的构造先验知识结合起来就可以结合地质模型来分析构造应力场的变化和预测储层天然裂缝。需要强调的是，上述针对二维剖面进行的一维曲率属性分析有着很大的局限性，在实际工作中要使解释结果能加真实的反映地下构造尤其是裂缝、孔洞等微小复杂构造时必须借助针对空间曲面上进行的二维曲率分析结果[4]。

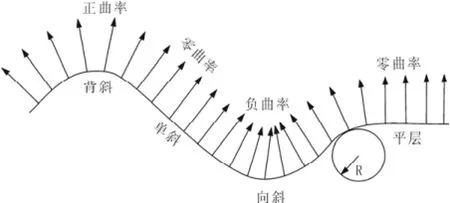
图3 曲率属性与地层形态的关系Fig.3 The relationship of curvature attribute to horizon

2 曲面曲率属性的分类

按照不同的算法，曲率可以分为很多种。不同算法的曲率属性以及用不同的参数计算的某一种曲率属性，可以不同程度反映断层、线性特征、局部形状等信息[5]。在此对常用的主要曲率属性定义及其物理和地质应用进行归纳：

（1）最大曲率、最小曲率 （Kmax、Kmin）

在无限个法线曲率中，绝对值最大的叫最大曲率（Kmax），而与之正交的叫最小曲率（Kmin），是对界面上每一点最大、最小弯曲的测量， Sigismundi和Soldo （2003年）认为最大曲率数据的时间切片上很容易看出断块的相对运动。

（2）平均曲率（Km）

过某一点两个相互垂直法曲率的平均值，就其属性上看与最大曲率类似。主要用它来求取其他的曲率属性。

（3）高斯曲率（Kg）

高斯曲率是最大最小两个主曲率的积，表达式如下： Kg=KmaxKmin。它描述了界面的弯曲度。在界面等量弯曲的情况下，高斯曲率的值不发生变化。换句话说，如果界面仅仅褶皱，没有断裂、拉伸和挤压（如把一张纸卷成柱形或锥形），高斯曲率总是零。这种性质，可以作为刻画断层的一种方法[6]。

（4）最正曲率和最负曲率（Kpos、Kneg）

在所有的可能的法线曲率中，最正值的曲率为最正曲率，最负值的曲率为最负曲率。这两种曲率突出了边界，主要用于显示断层。

（5）走向曲率（Kstrike）

沿着走向方向提取的曲率（垂直于提取倾向曲率的方向）叫走向曲率，有的文献中也其为切线曲率，它描述了界面的切线形态或形状。这种曲率将界面分成谷形区和脊形区。常常用于大范围的地形分析。

（6）倾向曲率（Kd）

沿着最大的倾角方向提取的曲率为倾向曲率，这种曲率是在倾角最大方向倾角变化率的测量，因此，也叫剖面曲率（profile curvature）。这种曲率对于断层的大小及方向均反映的较好。

（7）等值曲率（Kc）

假设对层面进行水平切割可以得到等值曲率，也称平面曲率，它可以用来描述与层面相关的各种等值线曲率。

（8）弯曲度（Kn）

弯曲度的值与层面形态无关，其值用来度量层面内曲率总量。

3 曲率属性分析与其他属性分析比较

目前曲率属性分析最为成熟的应用是进行断层识别，在此将其与其他几种主流断层识别方法进行别叫。除曲率属性分析以外，目前使用最为广泛的常规的断层识别技术包括：边缘检测、倾角、方位角、相干体及方差体等。这些基于一阶导数的方法其共同的缺点在于只能描述线性特征而未包含形状信息，因此不能区分非对称性构造（如断层）和对称性构造（如脊和谷）。相比之下，曲率属性分析用最小二乘法拟和二次曲面可较好解决这个问题[7]。

表1中对比了曲率属性分析法与倾角（边缘）、方位角、曲率几种常用断层识别方法的识别效果，从中可见相比于传统的基于一阶导数的方法，属性曲率分析法在描述对象两侧地层产状变化微小并且和断层倾向一致的情况下表现出明显的优越性[8]。

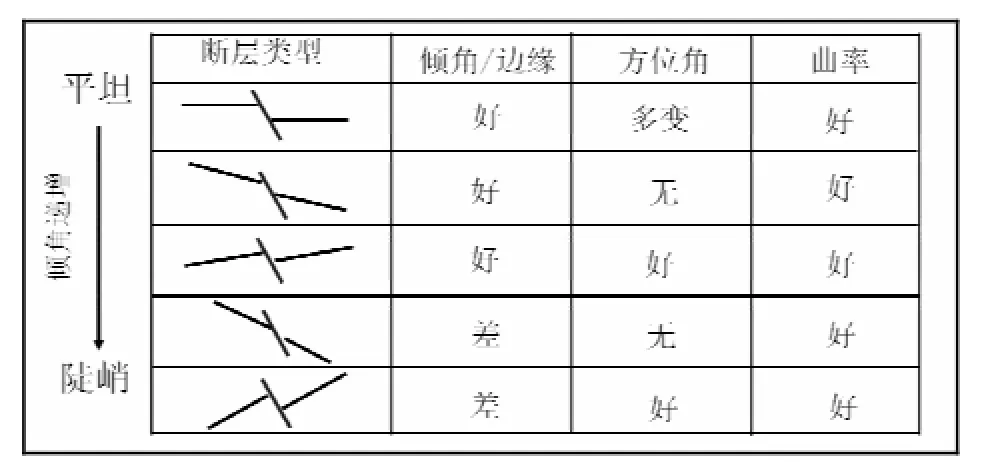
表1 几种属性分析方法断层描述能力对比Table 1 A comparison between several geometric attributes of their abilities to identify faults

从图4所示A、B两图的对比中我们可以看到，相比于倾角分析，曲率属性分析存在着如下几个方面的优势：（1）微小构造的向线性特征在曲率上更加清楚；（2）曲率可以揭示更多的线性特征（白圈内）；（3）曲率分析有助于删除局部的倾角作用，从而解决倾角饱和问题。B图中黑圈圈中部分由于局部高倾角背景的存在，在倾角属性上几乎看不到变化，而在A图所示的曲率属性图上线性特征很清楚[9]。

图4 某区域时间切片曲率属性分析与倾角分析的比较Fig.4 A comparison between time slices of dip and curvature attributes

4 曲率属性在地震资料解释中的应用实例

XX地区位于加拿大阿尔伯塔，研究目的层位于侏罗系，河道呈NW-SE向分布。图5(a)图为AA'任意线地震剖面，(b)图为相干时间切片，(c)图为最大正曲率时间切片，(d)图为最大负曲率时间切片。图中白色箭头所示为一条北西向展布的河道，在相干切片上河道的边界很清晰，在最大负曲率图上突出了河道的轴或河谷。最大正曲率属性则突出了河道的侧翼。但在工区的东南侧的河道（如黑色箭头所指）在相干图上就不那么清晰，而在最大负曲率属性上显示了河道的分叉现象。图中黄色箭头所指处为一条垂直相交的河道，在纵剖面上看的很清楚，在相干属性和最大负曲率属性图上也很清晰。而浅兰色箭头所指处河道在相干图上几乎看不见，但在最大负曲率图上河道的轴很清晰的呈现出来了。图中绿色箭头标示出了圆形决口区域，在最大正曲率属性图上清晰的显示为负值。

图5 曲率属性分析在河谷识别中的应用Fig.5 Application of curvature attribute to identify a valley

［1］王永刚.地震资料综合解释方法[M].东营:中国石油大学出版社,2007:66-80.

［2］Roberts A. Curvature attributes and their application to 3D interpreted horizons[J]. First Break, 2001, 19(2): 85-100.

［3］Hakami A M, Marfurt K J, Al-Dossary S. Curvature Attribute and seismic interpretation: Case study from Fort Worth Basin, Texas, USA. SEG Int'l Exposition and 74th Annual Meeting[C]. Denver, Colorado, 2004.

［4］Al-Dossary S, Marfurt K J. 3D volumetric multispectral estimates of reflector curvature and rotation[J]. Geophysics, 2006, 71(5): 41-51.

［5］王雷,陈海清,陈国文,等. 应用曲率属性预测裂缝发育带及其产状[J].石油地球物理勘探, 2010 ,45(6) :885-889.

［6］何英,贺振华,熊晓军.基于高精度曲率分析的断层识别方法[J]. 石油天然气学报,2010, 32(6):404-407.

［7］杨威, 贺振华, 陈学华. 三维体曲率属性在断层识别中的应用[J].地球物理学进展,2011,26(1):110-115.

［8］Chopra S, Marfurt K J. Integration of coherence and volumetric curvature images[J].The Leading Edge,2010,29(9): 1092-1107.

［9］陈学华, 贺振华, 杨威.地震资料的三维多尺度体曲率分析及应用[C]. 中国地球物理,北京:地震出版社,2010:524.

Analysis of Curvature Attribute and Its Application in Seismic Interpretation

LI Che，JI Tian-yu, LI Yu-che
（China University of Petroleum（Beijing）, Beijing 102249，China）

Analysis of curvature attribute is a new technology for seismic interpretation which has developed quickly in west countries in recent years. It shows good properties in identifying small fault, fracture and vugs existed underground. In this paper, based on the concept of curvature attribute, the basic theory and classification of the curvature attribute analysis were discussed. Then a comparison between the curvature attribute and other kinds of attribute analysis was carried out. Finally, actual application of curvature attribute analysis in seismic interpretation was introduced.

Curvature attribute; Seismic interpretation; Classification; Comparison

TE 122

： A

： 1671-0460（2014）04-0558-03

2013-10-11

李澈（1988-），男，黑龙江大庆人，在读硕士研究生，2011年毕业于中国石油大学（北京）自动化专业，现就读于中国石油大学（北京）地球物理与信息工程学院勘探地球物理专业，研究方向：地球物理勘探。E-mail：812894649@qq.com。